Магнитное поле. Основные теоретические положения, страница 12

Решение

Для расчета напряженностей в точках А и В  используем закон полного тока в интегральной форме и метод наложения, причем обе напряженности будем раскладывать на проекции в прямоугольной системе координат. С этой целью рассмотрим произвольную точку, положение которой определяется координатами  х  и  у  (рис. 14.42). Проекция напряженности поля в этой точке на ось х:

Hx(x,y) :=·.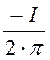

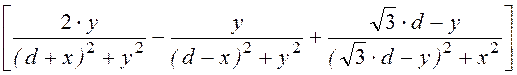Она состоит из трех составляющих, создаваемых левым, правым и верхним проводами линии, соответственно.

Аналогично проекция напряженности поля в этой точке на ось у:

Hy(x, y) :=·.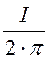

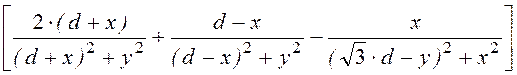Полные значения напряженностей в точках А и В:

H_A :=   H_B :=

Магнитное напряжение между точками определим в соответствии с соотношением: U_M =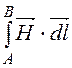.  Интегрирование выполним по горизонтали и вертикали. Тогда

U_M :=+.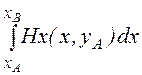

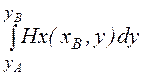MathCAD-программа и ответ приведены в Приложении к разделу 14.

ЗАДАЧА 14.33.  Рассчитать взаимную индуктивность двух двухпроводных линий, расположенных в воздухе (рис. 14.43), если

r₁ = 4 мм,   r₂ = 2 мм,   d₁ = 0,5 м,   d₂ = 0,2 м,  h₁ = 20 см,   h₂ = 30 см.

Решение

Расчет выполним, используя векторный магнитный потенциал4). Произведем вывод формулы для векторного магнитного потенциала вне цилиндрического проводника с током I.  Согласно уравнению Пуассона для магнитного поля  Ñ ²=.  Расписав выражение лапласиана в цилиндриче-ской системе координат и учитывая, что вектор  в данном случае имеет только одну составляющую =·A_z =·A, направленную по оси провода (по оси z), и эта составляющая зависит только от координаты r в силу симметрии, а также отсутствие плотности тока за пределами провода, получим

Ñ ²A =·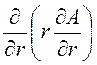= 0.

Двукратное интегрирование по r дает  A= C₀·lnr+ C₁. Вектор-потен-циал определяется с точностью до постоянной. Примем, что он равен нулю на поверхности провода, т.е. при  r= r₀.  Тогда  C₁= -C₀·lnr₀и  A=C₀·ln(r/r₀). Постоянную интегрирования С₀ определим, используя напряжённость маг-нитного поля, которая связана с вектор-потенциалом формулой  m_a·= rot.

Раскрыв выражение ротора в цилиндрической системе координат и учитывая, что =·Aи  = ·H,   получим  m_a·H= -,  откуда   H=-. На поверхности провода в соответствии с законом полного тока

H=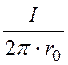.   Тогда     C₀ = -  и   A =.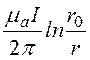

Для определения взаимной индуктивности линий предположим, что по проводам первой линии (1-1¢) замыкается ток  I,  как указано на рис. 14.43. Исходя из формулы  Ф =,  определим составляющую магнитного потока Ф₁, пронизывающую плоскость участка второй линии длиной  l  и создавае-мую током провода 1, а также составляющую Ф₂, создаваемую током провода  1¢:

Ф₁ =–=,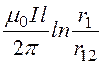

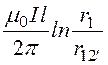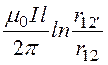Ф₂ =–=.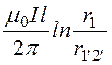

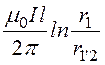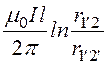Входящие в эти формулы расстояния (см. рис. 14.43):

r₁₂ = h₁;        r_12¢ =;      r_1¢2 =;

r_1¢2¢ =.

Поток взаимной индукции     Ф = Ф₁ + Ф₂ =.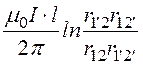

Взаимная индуктивность линий    М = =.

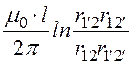При длине линий   l= 1 км    М =.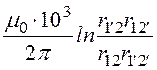

MathCAD-программа и ответ приведены в Приложении к разделу 14.

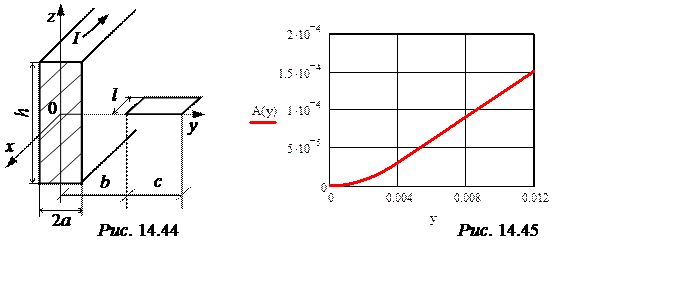
Задача 14.34. По уединённой плоской шине высотой  h = 15 см  и толщиной  2a = 0,8 см  протекает постоянный ток  I = 3600 А (рис. 14.44). Шина медная, расположена в воздухе. В плоскости х0у расположена прямоугольная рамка длиной  l = 0,5 м, причем сторона  l  параллельна оси  0х. Число витков рамки  w = 150,  b = 1 см,  с = 0,5 см.

1) Рассчитать зависимость векторного магнитного потенциала поля в функции координат и построить его график.

2) Используя векторный магнитный потенциал, рассчитать взаимную индуктивность шины и рамки.

Ответы: плотность тока в шине d = -3·10⁶ A/м²;

A(у) =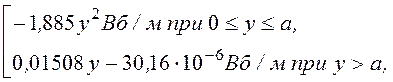     y [м];

график  A(у)  представлен на рис. 14.45; A(b) = 1,206·10 ^-4,    A(b+c) = 1,96·10 ^-4, магнитный поток сквозь рамку  Ф = l·(A(b+c) – A(b)) = 37,7·10 ^-4 Вб, взаимная индуктивность      М = Ф·w/I = 1,571 мкГн.

Пример MathCAD-программы, составленной в соответствии с алгоритмом решения задачи 14.21, приведен в Приложении к разделу 14.