Магнитное поле. Основные теоретические положения, страница 2

Результат решения занесем в табл. 14.1.

Таблица 14.1

Для внутренней области	Для наружной области

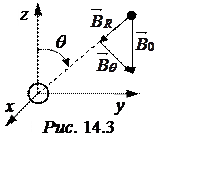Исследуем решение для наружной области, устремив  R ® ∞.  На таком расстоянии возмущающее действие внесенного шара исчезающее мало и согласно рис. 14.3   .

С другой стороны, 

B_{R e} = -m_em₀ C₄ cosq,  B_{q e} = m_em₀ C₄ sinq.

Последние два соотношения позволяют опреде-лить постоянную интегрирования

С₄ =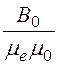==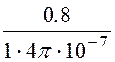 63,7.

Исследуем решение для внутренней области, устремив R ® 0. При этом ни напряженности  H_Ri  и  H_{q i}, ни индукции B_Ri и  B_{q i}, ни потенциал  j _Mi  не могут быть бесконечно большими. Поэтому  С₂ = 0.

Положим, что в центре внесенного шара  (R= 0)  j _Mi = 0.  Тогда С₃ = 0.

На этом этапе решение принимает вид, приведенный в табл. 14.2.

Таблица 14.2

Для внутренней области	Для наружной области

Постоянные интегрирования С₁ и С₅ определим из граничных условий при  R = R₀:   H_it = H_etи    B_in = B_en.

Уравнения принимают вид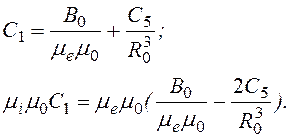         

Решение этой системы дает следующий результат:

С₁ =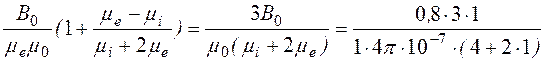= 31,85·10⁴ ,

С₅ =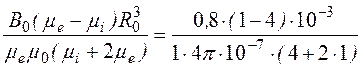= -318,5 A·м².

Постоянная интегрирования С₆ определяется из условия непрерывнос-ти потенциала на границе раздела сред, т.е. при   R= R₀ j_Mi = j_Mе:

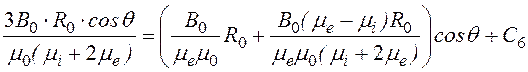,откуда  С₆ = 0.

Рассчитаем магнитную индукцию в точке М. Эта точка принадлежит внутренней области шара, и здесь

В_i == m₀m_i·С₁ =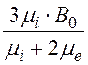==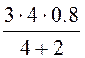 1,6 Тл.

Заметим, что внутри шара индукция является постоянной величиной и по направлению совпадает с В₀.   

Определим напряженность магнитного поля в точке N, находящейся во внешней области:

H_R =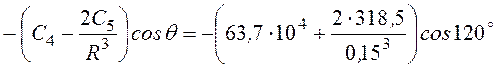= 41,29·10⁴;

H_q =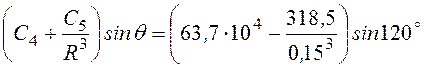= 47,03·10⁴;

H = ·10⁴ = 62,58·10⁴.

Эта напряженность одинакова для всех значений координаты a.

Задача 14.3. По прямолинейному цилиндрическому проводнику         (μ_r = 200),  расположенному в воздухе, протекает ток  I= 200 А,радиус проводаr₀ = 4 мм.

Требуется определить зависимость магнитной индукции в функции расстояния от оси проводника. Пользуясь полученными зависимостями, убе-диться, что магнитное поле внутри проводника вихревое, а вне – скалярное.

Ответ: при   0 ≤ r≤ r₀   B= 500r Тл, r [м];  , следовательно, поле вихревое; при  r₀ ≤ r< ∞  B= 4·10^-5/r Тл, r [м];  , следова-тельно, поле скалярное.

Задача 14.4. В равномерное магнитное поле с напряженностью           Н₀ = 120 А/см,   созданное в воздухе, помещен сферический магнитный экран с внутренним радиусом  а = 6 см  и наружным  b= 7 см.  Тело экрана выпол-нено из материала с относительной магнитной проницаемостью  μ_r = 400. Рассчитать коэффициент ослабления поля  K_осл = Н₁/Н₀, где  Н₁ – напря-женность поля внутри экрана.

Рассчитать K_осл для цилиндрического экрана с теми же размерами а и b.

Ответ:  для сферического экрана  K_осл =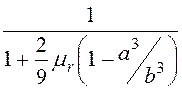= 0,029;

для цилиндрического экрана                     K_осл =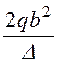= 0,0365, где  q=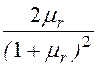= 0,004975;    D= b² – b ²·a² = 13,358;   b =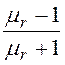= 0,9950.

14.3. РАСЧЁТ ПОЛЯ С ПОМОЩЬЮ ИНТЕГРАЛЬНЫХ СООТ-НОШЕНИЙ. ИСПОЛЬЗОВАНИЕ СКАЛЯРНОГО МАГНИТНОГО ПОТЕНЦИАЛА.

Задача 14.5. Рассчитать напряжённость магнит-ного поля, созданного уединённым цилиндрическим проводником с током  I  в однородной среде в точке А на расстоянии  r  от оси проводника (рис. 14.4).

Решение

Через точку А проведём окружность радиусом r и применим закон полного тока в интегральной форме

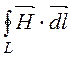= I.

Как видно из рис. 14.4, в силу симметрии направления векторов  и  во всех точках окружности совпадают, а значение напряжённости Н одинако-во. Тогда скалярное произведение векторов  и  заменяем произведением их модулей, а Н выносим за знак интеграла как константу. Получаем:

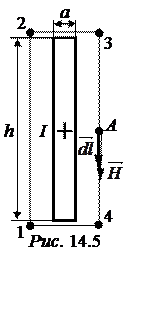
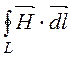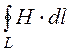== Н= Н·L = Н·2pr = I,

откуда  Н =.                      (14.1)

Задача 14.6. Рассчитать напряжённость магнитного поля, созданного уединённой плоской шиной размерами  а´h,  h >> а  с током  I  в однородной среде в точке А вблизи шины (рис. 14.5).

Решение