Магнитное поле. Основные теоретические положения, страница 14

Решение

Определим плотности тока в первой (r₁<r<r₂) и второй (r₂<r<r₃) областях, используя граничные условия. Так как  E_1t =E_2t  и векторы  и  в данном случае имеют только тангенциальные составляющие, то    .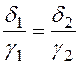

С другой стороны,     d₁(pr₂² – pr₁²) + d₂(pr₃² – pr₂²) = I.

Следовательно:          d₂= d₁,    d₁ =.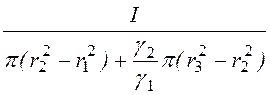

Для определения векторного магнитного потенциала применим уравне-ние Пуассона в цилиндрической системе координат. Так как вектор плотнос-ти тока имеет проекцию только на одну ось z, то и вектор  в данной задаче имеет только одну составляющую =·A, направленную по оси трубы (по оси z), и эта составляющая зависит только от координаты r в силу симметрии.

Тогда                                             для области внутри трубы 0;

Ñ  2A = =

для I области            -m_1a·d₁;

для П области           -m_2a·d₂;

для области вне трубы       0.

Двукратное интегрирование по r даёт:

A₀= C₀·lnr + C₁;      A₁ = -¼m_1аd₁r ²+ C₂·lnr + C₃;

A₂ = -¼m_2аd₂r ²+ C₄·lnr + C₅;     A₃ = C₆·lnr + C₇.

Слагаемое C₀·lnr должно отсутствовать, так как вектор  не может принимать бесконечно большие значения при   r= 0,   отсюда следует, что   C₀ = 0.  Вектор-потенциал определяется с точностью до постоянной. Примем, что на оси трубы  (r= 0)  он равен нулю, тогда  C₁ = 0и  A₀ = 0.

Для определения остальных постоянных интегрирования используем непрерывность вектор-потенциала:

1. При   r = r₁    A₀ = A₁.     Тогда      0 = -0,25m_1аd₁r₁²+ C₂·lnr₁ + C₃.

2. При  r= r₂A₁ = A₂, следовательно:          -0,25m_1аd₁r₂² + C₂·lnr₂ + C₃ = -0,25m_2аd₂r₂² + C₄·lnr₂ + C₅.

3. При  r= r₃A₂ = A₃,  то есть  -0,25m_2аd₂r₃² + C₄·lnr₃ + C₅ = C₆·lnr₃ + C₇.

С целью составления недостающего числа уравнений для определения постоянных интегрирования используем напряжённость магнитного поля, которую определим по формуле  m_a= rot.  Раскрыв выражение ротора в цилиндрической системе координат и учитывая, что =·Aи  = ·H, получим  m_a·H= -dA/dr, откуда

H₀ = 0;           H₁ =–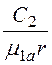,       H₂ =–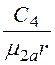,H₃ = -.

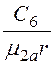На основании граничных условий получим:

4. При     r= r₁H₀ = H₁или     0 =–.

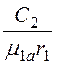5. При    r= r₂H₁ = H₂или     –=–.

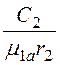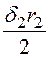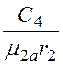6. При  r = r₃H₂ = H₃или     –= -.

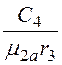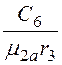Решение системы уравнений 1-6 даёт  C₂ … C₇.

Все расчёты и построение графика А(r) выполнены с помощью системы Mathcad. Они приведены в Приложении к разделу 14.

Для определения магнитного потока, замыкающегося по телу трубы, воспользуемся формулой    Ф =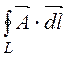.   В качестве контура интегрирования возьмём прямоугольник 1-2-3-4-1 (рис. 14.47), причём вдоль сторон 1-2 и 3-4   = 0, так как на этих участках угол между  и  равен 90°. Вдоль стороны  2-3    = 0, так как на внутренней поверхности трубы    А = 0.  Следовательно:     Ф =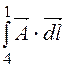= -А_{[r =r3]} ·l.

C. 133-139 – см. файл «Приложение к разделу 14».