Магнитное поле. Основные теоретические положения, страница 4

Н = d ·½а ==.

Индукция внутри шины      В = m_аН = m₀mdх. Магнитный поток сквозь сечение      dS = l·dx         dФ = В·dS = m₀mdхl·dx.    Этот магнитный поток сцеплен только с частью тока I, которая пропорциональна 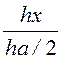 =,  поэтому магнитное потокосцепление  dY = dФ.  Внутренняя индуктивность

L_i ===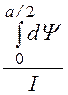=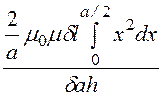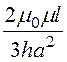х³=.

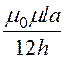Внутренняя индуктивность не зависит от размеров шины, если пропорция  h/a  сохраняется.

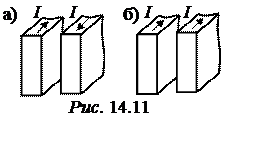 В случае двух шин, если токи в них направлены в разные стороны (рис. 14.11,а), шины оказываются соединенными последовательно, и их внутренняя индуктивность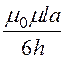

L_iS = 2·L_i =;

если токи направлены в одну сторону (рис. 14.11,б), шины соединены параллельно и тогда

L_iS = ½·L_i =.

Задача 14.11. По металлической трубе, материал которой обладает магнитной проницаемостью m_r и находящейся в воздухе, замыкается ток I, как показано на рис. 14.12. Рассчитать магнитное поле  внутри, вне и в теле трубы.

Решение

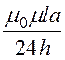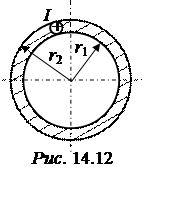
Расчет произведем с помощью закона полного тока в интегральной форме. В качестве контура интегрирования возьмем окружность радиуса r, центр которой совпадает с осью трубы. Для области, находящейся внутри трубы  (0 ≤ r ≤ r₁),  полный ток равен нулю, поэтому здесь напряженность Н и индукция В равны нулю.

B теле трубы  (r₁ ≤ r ≤ r₂) 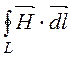  =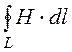= H= H·2pr, а полный ток равен  d ·S,   где  d– плотность тока в теле трубы, а  S – площадь кольца с радиусами  r₁  и  r.  Поскольку  d =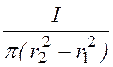;   S = p(r² –),  то

Н =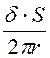=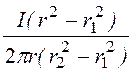,   а   В = m₀m_rН =.

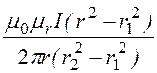Вне трубы (r₂ ≤ r ≤ ∞) 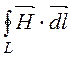 = H ·2pr,  а полный ток равен   I, следо-вательно,   Н =   и    В =.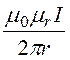

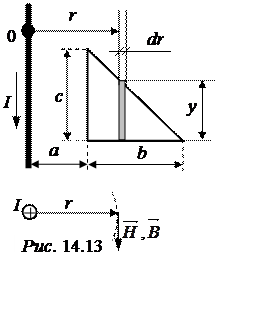
Задача 14.12. Плоская треугольная рамка (рис. 14.13) имеет  w = 400 витков и находится в среде с проницаемостью   m = 10   в одной плоскос-ти с длинным круглым проводом радиуса  r₀.  Размеры:  а = 10 см,  b = 20 см,  c = 15 см. Опреде-лить взаимную индуктивность провода и рамки.

Решение

По определению   M₁₂ == M₂₁ == М. В данном случае удобнее задаться некоторым током I в проводе и рассчитать магнитный поток сквозь рамку.

На расстоянии r от провода в треугольнике выделим элементарную площадку  dS = y·dr.  Получим формулу магнитного потока сквозь неё.

y = k·r + d;    k = -;    d =(a + b);

H =;      B =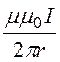;     dФ = B·dS = B·y·dr =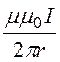(-r +(a + b))dr.

Ф = ==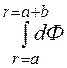

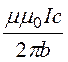
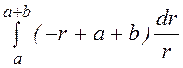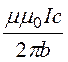=[-r + (a + b)ln(r)] =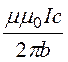[-b + (a + b)ln];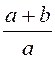

Y= w·Ф;   M ==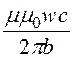[-b + (a + b)ln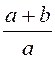] = 77,75 мкГн.

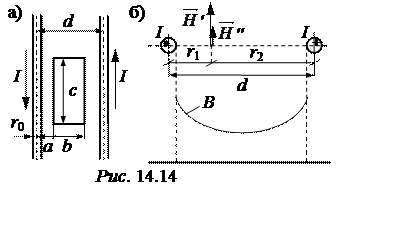Задача 14.13. Энергия магнитного поля между проводами двухпроводной воздушной линии на единицу её длины (рис. 14.14,а)  W = 6∙10^-3 Дж/м; r₀ = 3 мм; d = 40 см.

Требуется: а) определить ток в проводах линии, построить график изменения магнитной индукции  между проводами; б) рассчитать взаимную индуктивность линии и прямоугольной рамки с числом витков    w= 200,  находящейся в одной плоскости с линией, если  а = 10 см;  b= 20 см;  c= 30 см.

Решение

Энергия магнитного поля между проводами линии   W=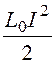, где   L₀ – внешняя индуктивность единицы длины линии.

Предположим, что по проводам линии протекает ток I как показано на рис. 14.14,б. По закону полного тока с использованием метода наложения определим составляющие напряженности поля Н¢ и Н¢¢, направление которых определяется правилом правоходового винта и они перпендикулярны плоскости двухпроводной линии, затем магнитную индукцию и магнитный поток между проводами (внешний по отношению к проводам). Для этого расстояние от оси левого провода обозначим r₁, а от оси правого – r₂. Тогда в соответствии с (14.1) и (14.3)

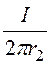Н¢ =;   Н¢¢ =;    В¢ =;   В¢¢ ==;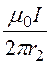

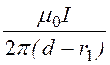Ф¢ = Ф¢¢ =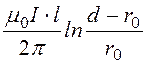;    Ф = Ф¢ + Ф¢¢= .

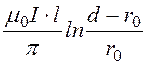Примерный вид графика изменения магнитной индукции между проводами   В = В¢+ В¢¢ показан на рис. 14.14,б.

В рассматриваемом случае d>> r₀, поэтому с достаточной степени точности можно положить, что  Ф =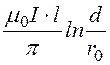,  а внешняя индуктивность единицы длины линии

L₀ =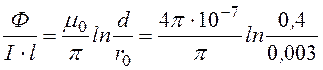 = 19,57·10 ^-7 Гн/м.

Тогда ток в проводах линии    I =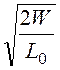 = 78,31 А.

Взаимная индуктивность провода и рамки  M =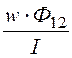,  где Ф₁₂ – магнитный поток, сцепленный с витками рамки. Его определим согласно формуле (14.3):