Магнитное поле. Основные теоретические положения, страница 13

Задача 14.35. Постоянный ток    I= 600 А  замыкается по двухпроводной воздушной линии, выполненной шинами прямоугольного сечения с размерами  а = 4 мм,  h= 200 мм (рис. 14.46). Магнитная проницаемость левой шины  m_r1 = 800, а правой  m_r2 = 400.

Построить графики зависимости векторного маг-нитного потенциала и напряженности магнитного поля в функции координат. Определить магнитный поток, замыкающийся по телу левой шины длиной   l = 1 м.  Рассчитать внутреннюю индуктивность единицы длины линии.

Решение

Выберем расположение декартовой системы координат как показано на рис. 14.46. Для определения векторного магнитного потенциала применим уравнение Пуассона. При этом учтем, что поскольку толщина шин и расстояние между ними значительно меньше их высоты, то можно пренебречь краевым эффектом. Так как вектор плотности тока имеет проекцию только на ось z, то и вектор  в данной задаче имеет только одну составляющую , направленную вдоль шин, а зависит она только от координаты  х.

Определим величину плотности тока в шинах   d=.

Тогда с учетом того, что в правой шине вектор  направлен вдоль оси z, а в левой – в противоположном направлении, получим

Ñ ²A == 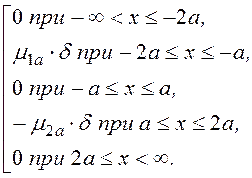                                      (1)

Двукратное интегрирование (1) по x даёт

А₀ = С₀х + С₁;   А₁ = 0,5m_1аd х² + С₂х + С₃;     А₂ = С₄х + С₅;

А₃ = -0,5m_2аd х² + С₆х + С₇;     А₄ = С₈х + С₉.                                               (2)

Учитывая, что вектор-потенциал определяется с точностью до постоянной величины, примем   А₂ = 0   при   х = 0.  Тогда  С₅ = 0.

Для определения остальных постоянных интегрирования используем непрерывность вектор-потенциала, а именно:

при  х = -2а  А₀ = А₁  или       С₀(-2а) + С₁ = 0,5m_1аd(-2а)² + С₂(-2а) + С₃;         (3)

при  х = -а    А₁ = А₂  или       0,5m_1аd(-а)² + С₂(-а) + С₃ = С₄(-а)+ С₅;                (4)

при  х = а     А₂ = А₃  или       С₄·а + С₅ = -0,5m_2аd а² + С₆а + С₇;                        (5)

при  х = 2а  А₃ = А₄   или       -0,5m_2аd(2а) + С₆(2а) + С₇ = С₈(2а) + С₉.             (6)

С целью составления недостающего числа уравнений для определения постоянных интегрирования используем напряженность магнитного поля, которая связана с вектором  таким соотношением  .

Раскрыв выражение ротора в декартовой системе координат и учитывая, что    и  , получим 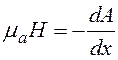   или

Н₀ = -;     Н₁ = d ·x – ;    Н₂ = -;    Н₃ = -d ·x – ;     Н₄ = -.

Используя закон полного тока в интегральной форме, для нашего устройства имеем

Н₀ = 0,   Н₂ = -,   Н₄ = 0.                                               (7)

Кроме того, на основании граничных условий

при   х = -2а    Н₀ = Н₁,      а при   х = 2а    Н₃ = Н₄.                  (8)

Тогда из системы уравнений  (3)…(8) получаем   С₀ … С₉.

Все расчёты и построение графиков А(х) и Н(х)  выполнены с помощью системы Mathcad. Они приведены в Приложении к разделу 14.

Магнитный поток, замыкающийся по телу шин, определим используя формулу Ф =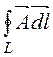. В качестве контура интегрирования возьмем прямоуголь-ник А-В-С-D-А (рис. 14.46). Вдоль сторон АВ  и  СD  = 0, так как на этих участках векторы  и   взаимно перпендикулярны. Вдоль стороны ВD векторы   и   сонаправлены, а вдоль стороны СА они противоположны по направлению, поэтому   Ф = (А_(х=-а) – А_(х=-2а))l.

Для определения внутренней индуктивности аналогично определим магнитный поток, замыкающийся по телу правой шины   Ф¢ = (А_(х=2а) – А_(х=а))l.

Тогда внутренняя индуктивность единицы длины линии

L_i=.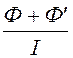

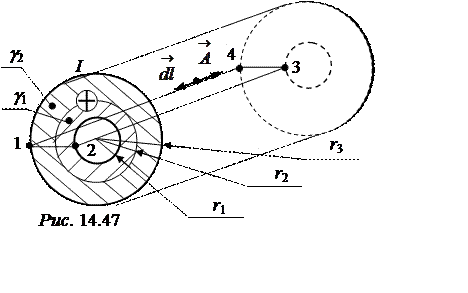
ЗАДАЧА 14.36. по весьма длинной биметалличе-ской трубе (рис. 14.47) про-текает постоянный ток I=1кА.  Проводимость внутреннего слоя g₁, а внешнего  g₂ = 1,5·g₁.  Магнитная проницаемость внутреннего слоя   m_1a = 10m₀,  наружного –  m_2a = m₀.  по-строить график зависимости векторного магнитного потенциала от расстояния до центра трубы. Определить магнитный поток, замыкающийся по телу трубы длиной 1 м, если    r₁ = 10 см, r₂ = 15 см,r₃ = 20 см.