Электрические цепи с распределёнными параметрами в установившемся РЕЖИМЕ

8. Электрические цепи с распределёнными параметрами

8.1. Электрические цепи с распределёнными параметрами в установившемся РЕЖИМЕ

8.1.1. Основные теоретические положения

Устройства или электрические цепи, в которых токи i(x,t) и напряжения u(x,t) являются функциями не только времени t, но и зависят от координаты x, называют длинными линиями или линиями с распределёнными параметрами (ЛРП). Факторами, которые обусловливают распределённость параметров, являются значительная протяжённость устройства в пространстве, высокое напряжение, высокая частота. Примерами ЛРП являются: линии электропередач напряжением 110 кВ и выше, короткие линии связи у микрофона, кабель телеантенны, сами антенны радио и телепередатчиков, устройства задержки сигналов, гирлянды изоляторов.

Исходными характеристиками или первичными параметрами длинных линий являются:

- r₀, Ом/м – продольное сопротивление линии на единице длины;

- g₀, См/м – поперечная проводимость линии, причём   g₀ ¹ r₀^-1;

- L₀, Гн/м  и  C₀, Ф/м, соответственно, – индуктивность и емкость линии на единице длины.

Если параметры r₀, g₀, L₀, C₀  одинаковы по всей длине линии, то линия называется однородной. В справочной литературе существуют формулы, по которым можно рассчитать первичные параметры линии по известным конструктивным параметрам.

Наиболее общие уравнения двухпроводной линии, которые справедливы для любого режима работы, имеют вид:

-= r₀·i + L₀,

-= g₀·i + C₀.                                         (8.1)

Если же линия работает при синусоидальных токах и напряжениях, то уравнения упрощают, сводя их в комплексной форме к одному дифференциальному уравнению второго порядка с нулевой правой частью. Решение таких уравнений можно записать для действующих и мгновенных значений напряжения и тока в любой точке, отстоящей на расстоянии x от начала линии или на расстоянии у от её конца:

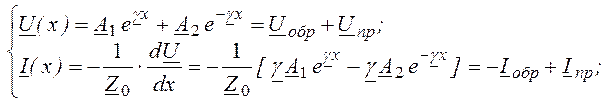                (8.2)

u(x,t) =A₁e^ax·sin(wt + y_обр + bx) +A₂e^–ax·sin(wt + y_пр – bx);                (8.3)

i(x,t) = -e^ax·sin(wt + y_обр – j_C + bx) +e^–ax·sin(wt + y_пр – j_C – bx);

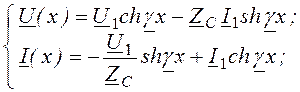
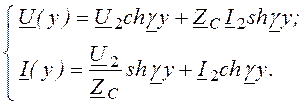                  (8.4)

Здесь:    Z₀ = r₀ + jwL₀, Ом/км,     Y₀ = g₀ + jwC₀, Cм/км;

Z_C = Z_C·=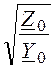, Ом – характеристическое (волновое) сопротивление линии;

g  = = a + jb , 1/км – коэффициент распространения волны в линии;

a, Нп/км   – коэффициент затухания волны;

b, рад/км  – коэффициент изменения фазы волны в линии;

A₁,  A₂,  y_пр,y_обр – постоянные интегрирования;

U₁, U₂, I₁, I₂ – напряжение и ток, соответственно, в начале и в конце линии.

Величины Z_С и g  называют вторичными параметрами линии, их  можно рассчитать через первичные параметры линии  r₀, g₀, L₀, C₀, и наоборот.

Из уравнений (8.3) для мгновенных значений следует, что в любом сечении линии ток и напряжение есть наложение двух встречных затухающих синусоид-волн – прямой (падающей) и обратной (отражённой). Иными словами: в линии имеют место волновые процессы, причём:

u(x,t) = u_пр + u_обр;     i(x,t) = i_пр – i_обр.                                  (8.5)

Бегущую электромагнитную волну можно охарактеризовать напряжением, током, длиной волны l и фазовой скоростью её распространения v:

l= 2p /b = v /f,        v = w /b.                                (8.6)

Поскольку коэффициент фазы b выражается через w, Z₀, Y₀, то длина волны и скорость её распространения зависят от частоты и параметров самой линии.

Для воздушных линий характерно:

Z_С > 150 Ом,    v ≈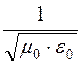= c = 300×10³ км/с, для кабельных линий обычно:     Z_С < 120-150 Ом, v ≈ ½c = 150×10³ км/с.

Входное сопротивление и параметры линии могут быть определены по её конструктивным параметрам (по справочным данным) или по результатам опытов холостого хода и короткого замыкания (Z_Н – сопротивление нагрузки, l – длина линии):

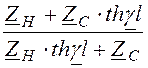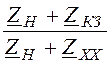Z_ВХ == Z_С·= Z_ХХ ·;    Z_ХХ =;    Z_КЗ = Z_c×thg l.

Через сопротивления Z_ХХ и Z_КЗ вторичные, а затем и первичные параметры линии определяются по выражениям:

Z_С=;               thg l =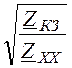;  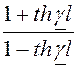   = е^2al·е ^j2bl;       (8.7)

g ×Z_C =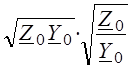= Z₀=R₀ + jωL₀;       g /Z_C = Y₀ = g₀ + jωC₀.        (8.8)

Отношение напряжения падающей волны в конце линии к напряжению отражённой волны в конце линии называется коэффициентом отражения волны:

K =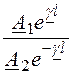=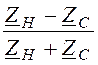.                                      (8.9)

Соотношения для линий при согласованной нагрузке  Z_н = Z_с:

Z_ВХ = Z_с;η = е ^-2αl; 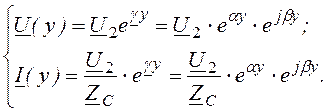      (8.10)

В технике связи, где возможны сигналы широкого диапазона частот, выделяют понятия линии без искажений сигналов (ЛБИ), в которой сигналы на всех частотах распространяются с одинаковой скоростью и затухают в равной степени, и линии без потерь (ЛБП), в которой  wL₀ >> r₀,  wC₀ >> g₀  и величинами  r₀,  g₀  можно пренебречь.

Соотношения для ЛБИ:

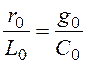;   a =¹ f(w),   b= w;   v =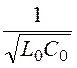¹ f(w), характеристическое сопротивление   Z_c =   резистивное.          (8.11)

Соотношения для ЛБП:   r₀ = 0,   g₀ = 0;  a = 0 ¹ f(w),   b= w;

v =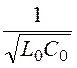¹ f(w);     ЛБП является частным случаем ЛБИ;

характеристическое сопротивление   Z_c =   резистивное;

основные уравнения ЛБП: 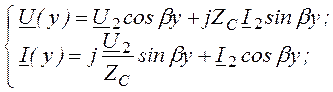                   (8.12)

входное сопротивление ЛБП:

Z_вх =Z_c·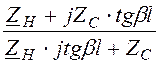,     Z_хХ = -j;    Z_КЗ = jZ_c·tgbl.         (8.13)