Определить: 1) при каком сопротивлении приёмника в линии отсутствует отражённая волна на средней расчётной частоте 800 Гц; 2) напряжение, ток, активную мощность источника и КПД линии длиной 59 км, если напряжение на нагрузке равно 20 В, а её сопротивление – как в п.1.
Решение
Вычислим вторичные параметры линии на частоте
ω = 2pf = 2p ·800 = 5027 рад/с:
ZC =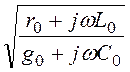
=
=
=
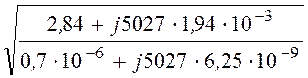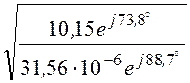= 567×e –j7,46° Ом,
g =
=
=
= 17,9×10 –3×e j81,3° 1/км.
Отсюда коэффициент затухания – a = Re(g) = 2,71×10 –3 Нп/км.
Отражённая волна в линии отсутствует, если линия согласована с нагрузкой, то есть если её сопротивление ZН = ZC = 567×e –j7,46° Ом.
Тогда напряжение, ток и мощность в конце линии:
u2 =
20 В, I2=
=
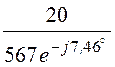= 0,0353×e j7,46° А,
Р2 = Re(u2·
)= 20·0,0353·cos (-7,46°) = 0,7 Вт.
При согласованной нагрузке КПД линии можно вычислить по формуле
η = e –2al = e –2·2,71·0,059 = 0,73.
Мощность в начале линии Р1 = Р2/η = 0,7/0,73 = 0,96 Вт.
Напряжение и ток в начале линии
u1 = u2·e al = 20·e al = 20e 2,71·0,059 = 23,4 В,
I1 = I2·e al = 0,0353·e 2,71·0,059 = 0,041 А.
Задача8.16. Генератор постоянного тока с напряжением 10 кВ питает последовательно соединённые воздушную линию и кабельную. Параметры воздушной ЛРП: l1 = 20 км, r01 = 4 Ом/км, g01 = 1∙10 -6 См/км. Параметры кабеля: l2 = 40 км, r02 = 0,5 Ом/км, g02 = 0,5∙10 -6 См/км. Кабель имеет согласованную нагрузку. Определить мощности генератора и приёмника, КПД воздушной линии, кабеля и всей линии.
Ответы: Рген = 94,3 кВт, РH = 82,2 кВт,
η1 = 0,907; η2 = 0,96; ηобщ= 0,872.
Задача8.17. По силовой ЛЭП длиной 50 км передаются сигналы автоматики и телемеханики. На частоте сигнала коэффициент затухания α = 96 мНп/км, а ZС = 640е -j10° Ом. На частоте сигнала приёмник согласован с линией. Уровень сигнала в начале линии (по мощности) равен 4,6 Нп. Определить напряжение сигнала на приёмном устройстве.
Решение
Определение. Мощность сигнала в любой точке линии может быть задана в виде «уровня сигнала в неперах» по отношению к сигналу мощностью 1 мВт, уровень которого принят равным нулю.
1. По условию задачи уровень сигнала в начале линии α = 4,6 Нп. Так как
α = ½ lп 
= 4,6 Нп, где
Р0 = 1 мВт, то Р1 = е
2α = е 2∙4,6 = 9897 мВт.
2. Общее затухание сигнала в линии αl = 96∙10 -3∙50 = 4,8 Нп.
Следовательно, уровень сигнала у приёмника αпр = 4,6 – 4,8 = -0,2 Нп, а его мощность Р2 = е 2∙(-0,2) = е -0,4 = 0,67 мВт.
3. Приёмник согласован с линией, т.е.
ZН = ZС = 640е -j10° = 630,3 – j111,1 Ом = Z1.
Напряжение сигнала на входе линии целесообразно рассчитать через проводимость по выражению Р = g∙U 2:
Yн = 1/ZН = (1,539 + j0,271)∙10 -3 См, gH = Re(Yн) = 1,539∙10 -3 См.
Тогда
U1 =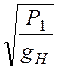 
= 
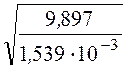= 80,2
В,
U2 = U1∙е -аl = 80,2∙е -4,8 = 0,66 В.
Задача 8.18. Мощность передающего устройства 1 мВт. На приёмник, согласованный с линией, имеющей α = 0,02 Нп/км, необходимо передать сигнал мощностью не менее 1 мкВт.
Определить допустимую дальность связи и соотношение напряжений U1/U2 сигнала на входе и на выходе линии.
Ответы: l = 173 км, U1/U2 = 31,62.
8.1.4. Линии без искажений
Задача8.19. Воздушная двухпроводная линия связи длиной 100 км имеет параметры: r0 = 2,8 Ом/км, g0 = 0,7 мкСм/км, L0 = 2 мГн/км и работает в согласованном режиме при частоте ω = 5000 рад/с. Какую дополнительную индуктивность L0¢ необходимо включить на каждый километр длины линии, чтобы в ней не было искажений, а выходное напряжение отставало от входного на 100° по фазе?
Решение
По условию сдвиг фаз в линии составляет
βl= 100° + 360°·k = 1,745 + 2pk рад, то есть β = (1,745 + 2pk)·10 -2 рад/км.
Оценим значение β. Фазовая скорость в воздушной
линии практически равна скорости света, поэтому β »
=
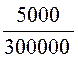= 1,667·10 -2
рад/км.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.