Сопоставляя два полученных ответа, приходим к выводу, что k = 0.
Окончательно получаем β = 0,01745 рад/км.
Для неискажающей линии справедливы следующие соотношения
β = ω![]() и
и 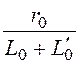 =
=![]()
или ![]() =
=![]() и
и 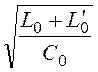 =
=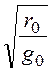 .
.
Перемножая последние два равенства, находим
(L 0 + L0¢) =![]()
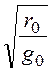 =
=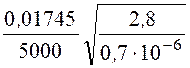 =
0,00698 Гн/км.
=
0,00698 Гн/км.
И наконец, получаем: L0¢ = 6,98 – 2 = 4,98 мГн/км.
Задача 8.20. Кабельная линия связи имеет длину 150 км и волновое сопротивление ZC = 60 Ом. Эту линию сигналы проходят за 1 мс без искажений, затухая при этом на 11,3 дБ. Определить первичные параметры линии.
Решение
Затухание в линии составляет al = 11,3 дБ = 11,3·0,115 = 1,3 Нп.
Отсюда коэффициент затухания a=![]() =
=![]() = 8,66·10 -3 Нп/км.
= 8,66·10 -3 Нп/км.
В то же время, для линии без искажений справедливы соотношения:
![]() =
=![]() ,
ZC =
,
ZC =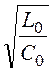 , a=
, a=![]() , v=
, v=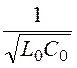 .
.
Причём для кабельной линии можно принять v= 150 000 км/с.
Из этих соотношений находим:
r0 = a ·ZC = 8,66·10 -3·60 = 0,52 Ом/км,
g0 =![]() =
=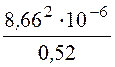 = 1,44·10 -4 См/км,
= 1,44·10 -4 См/км,
L0 =![]() =
=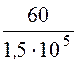 = 0,4·10 -3 Гн/км = 0,4 мГн/км,
= 0,4·10 -3 Гн/км = 0,4 мГн/км,
C0 =![]() =
=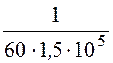 = 0,111·10 -6 Ф/км =
0,111 мкФ/км.
= 0,111·10 -6 Ф/км =
0,111 мкФ/км.
Задача8.21. Первичные параметры двухпроводной медной 4-миллиметровой телефонной линии (при f = 100 кГц): r0 = 14 Ом/км, L0 = 2·10 -3 Гн/км, g0 = 5·10 -6 См/км,C0 = 6,36·10 -9 Ф/км. Вычислить индуктивность L1, которую надо включить на каждый километр длины, чтобы линия стала неискажающей. Чему при этом будут равны вторичные параметры линии?
Ответы: L1 =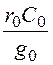 –
L0 =
15,8·10 -3 Гн/км,ZC =
–
L0 =
15,8·10 -3 Гн/км,ZC =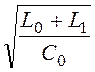 = 1673 Ом,
= 1673 Ом,
g= a+ jb=![]() + jw
+ jw ![]() = 8,37·10 -3 + j6,685 1/км.
= 8,37·10 -3 + j6,685 1/км.
Задача8.22. К неискажающей линии, полученной в задаче 8.21, подведено напряжение и1 = (10sin(2p·105t) + 5sin(4p·105t)) B. Определить мгновенное значение напряжения в конце линии длиной l = 100 км при согласованной нагрузке и при холостом ходе. Указать, сохраняется ли неискажённость передачи.
Ответы: g(w) = 6,685·е j 89,93º 1/км; g(2w) = 13,37·е j 89,96º 1/км;
при
Z2 =ZC: U2m = U1m·e -gl; и2 = (4,33sin(2p·105t–
143,73º) + 2,17sin(4p·105t+
+ 72,54º)) B, неискажённость сохраняется, так как ![]() /
/![]() =
=![]() /
/![]() = = 0,433 и y(1)·2 =
y(2) (-143,73·2º
= -287,46º; -287,46º+360º = 72,54º);
= = 0,433 и y(1)·2 =
y(2) (-143,73·2º
= -287,46º; -287,46º+360º = 72,54º);
при
ХХ: U2m = U1m/ch(gl); и2 = (8,09sin(2p·105t–
153,35º) + 5,08sin(4p·105t+
+ 65,31º)) B, неискажённость не сохраняется, так как ![]() /
/![]() = 0,809 ¹
= 0,809 ¹![]() / /
/ /![]() = 1,02
и y(1)·2
¹ y(2) (-153,35·2º = -306,70º; -306,70º+360º
= 53,3º ¹ 65,31º).
= 1,02
и y(1)·2
¹ y(2) (-153,35·2º = -306,70º; -306,70º+360º
= 53,3º ¹ 65,31º).
8.1.5. Линии без потерь
Задача 8.23. Вольтметр, включенный в конце воздушной линии без потерь, показывает 100 В. Определить показание амперметра на расстоянии 2 м от конца линии, если частота генератора f = 3·10 7 Гц, а волновое сопротивление линии ZC = 1000 Ом.
Решение
В конце линии включен вольтметр, обладающий большим сопротивлением. Следовательно, линия работает в режиме холостого хода, и ток в конце линии i2 = 0, поэтому одно из основных уравнений ЛБП (8.11) принимает вид:
i(y) = j![]() sin(βy).
sin(βy).
Фазовая скорость в воздушной линии практически равна скорости света с = 3·108 м/с. Тогда коэффициент фазы линии:
β =![]() =
=![]() =
=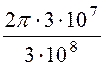 =
0,2p рад/м.
=
0,2p рад/м.
Таким образом, показание амперметра
iА = |i(y=2)| =![]() sin(βy) =
sin(βy) =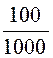 sin(0,2p ·2) = 0,0951 A.
sin(0,2p ·2) = 0,0951 A.
Задача8.24. Генератор с длиной волны λ = 20 м включён на идеальную ЛБП длиной l = 5 м. В конце линии включён амперметр, который показал ток 0,17 А, а в середине линии включён вольтметр, который показал 120 В. Определить волновое сопротивление линии. Принять rv = ∞, rА = 0.
Решение
Уравнение линии без потерь в режиме короткого замыкания имеет вид:
U(у) = jZС∙I2∙sin(βу).
Для середины линии sin(βу) = sin(![]() ∙
∙![]() λ = 0,25π
= 45°) = 0,7071.
λ = 0,25π
= 45°) = 0,7071.
Тогда сопротивление ZС = 120/(0,17∙0,7071) = 998 Ом.
Задача8.25. Определить параметры воздушной линии без потерь длиной 30 м с волновым сопротивлением 600 Ом, работающей на частоте 15 МГц. При сопротивлении нагрузки 300 Ом и напряжении U2 = 120 В рассчитать мощность, поступающую в линию, и её КПД.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.