В курсе ТОЭ основы теории ЛРП рассматриваются применительно к однородным двухпроводным линиям, работающим при синусоидальных токах и напряжениях. Все расчетные соотношения могут быть распространены на симметричные трехфазные линии с учётом одной фазы, а также на линии постоянного тока. Линиям постоянного тока индуктивность L0 и ёмкость C0 также присущи, но не проявляют себя. Здесь учитываются лишь параметры r0, g0.
Линия с распределёнными параметрами является симметричным четырёхполюсником. Поэтому, сопоставляя уравнения ЛРП (8.4) при у = l с уравнениями четырёхполюсника формы А (см. /1/, разд. 5)
U1 = А·U2 + В·I2; I1 = C·U2 + D·I2, получаем следующие соотношения:
А = D = сhg l, В = Zc×shg l, C =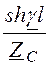
.
(8.14)
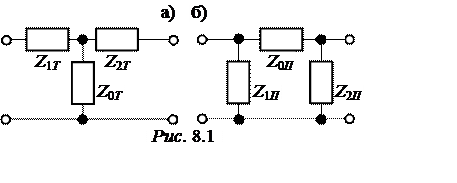
ЛРП как четырёхполюсник может быть представлена Т- или П- эквивалентной схемой (рис. 8.1), сопротивления которых вычисляются по формулам:
Z1T =Z2T =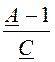
= ZС×
;
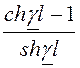Z0T =
=
;
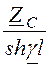Z1П =Z2П =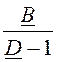
=ZС×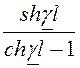
; Z0П = В
= Zc×shg l.
(8.15)
8.1.2. Расчёт параметров линии и её режимов работы
Задача8.1. Для определения параметров линии связи длиной 160 км на частоте 1000 Гц поставлены опыты холостого хода и короткого замыкания, в результате которых получено: ZХХ = 887·е -j35° Ом, ZКЗ = 540·е j21° Ом. Определить первичные и вторичные параметры линии.
Решение
1. Определяем вторичные параметры линии.
Zс =
= 692·е -j7° Ом, th gl =
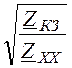= 0,780·е j28° = 0,688 + j0,366;
= 
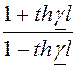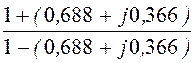= 3,6·е j61,83°
= j1,08 рад = е 2αl·е j2βl.
Это равенство распадается на два: е 2αl= 3,6
и 2βl = 1,08 + 2πk.
Из первого равенства находим коэффициент затухания
2αl= lп е 2αl= lп 3,6 = 1,281, α = 0,004 Нп/км.
Чтобы оценить число k полных 2π радиан на всей длине линии, определим ориентировочно при v = 300∙10 3 км/с общий сдвиг по фазе на всей длине линии:
2β¢l
= 2l∙ 
= 2∙160∙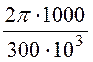
= 6,702 рад > 2π , k
= 6,702/6,283 ≈ 1.
Следовательно: 2βl = 1,08 + 2π∙1, откуда β = 0,023 рад/км.
Таким образом, Zс = 692·е -j7° Ом,
γ = α + jβ = 0,004 + j0,023 = 0,0233е j80,13° 1/км.
2. Определяем первичные параметры линии:
Z0 = r0 + jwL0 =g ×Zc = 0,0233е j80,13°∙692е -j7° = 16,12е j73,13° = 4,68 + j15,43 Ом,
Y0 = g0 + jwC0 = g /Zc = 0,0233е j80,13°/(692е -j7°) =
= 33,67∙10 -6·е j87,13° = (1,68 + j33,63)∙10 -6 См/км.
С учётом частоты w = 2π∙f = 6283 рад/с окончательно получаем:
r0 = 4,68 Ом/км, g0 = 1,68∙10 -6 См/км,
L0 = 15,43/6283 Гн/км = 2,46 мГн/км, C0 = 33,63∙10 -6/6283 Ф/км = 5,35 нФ/км.
Задача8.2. Из опытов холостого хода и короткого замыкания для линии связи длиной l= 120 км на частоте 800 Гц найдено: ZХХ = 182е j3,55° Ом, ZКЗ = 209е -j22,1° Ом. Требуется определить вторичные и первичные параметры линии, а также вычислить входное сопротивление линии, если её нагрузить на ZН = 2ZС.
Ответы: ZС = 195е -j9,28° Ом, γ = 8,93∙10 -3 + j18,40∙10 -3 1/км;
r0 = 2,3 Ом/км, g0 = 30∙10 -6 См/км, L0 = 0,65 мГн/км, C0 = 20 нФ/км,
ZВХ = 191е -j5° Ом.
ЗАДАЧА 8.3. Экспериментальным путём удалось получить некоторые параметры линии связи длиной l =140 км, работающей на частоте f =1500 Гц: ZC = 710×e -j9° Ом, Z0 = 19,2×e j70° Ом/км. Требуется рассчитать первичные и вторичные параметры, определить входное сопротивление в режиме холостого хода и в режиме короткого замыкания.
Решение
Угловая частота w = 2pf = 2p ×1500 = 9425 рад/с.
Поскольку Z0 = r0 + jwL0 = 6,57 + j18,04 Ом/км, то первичные продольные параметры
r0
= Re(Z0)
= 6,57 Ом/км, L0 =
Im(Z0) =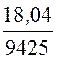
= 1,91×10 –3 Гн/км.
Далее из ZС =
находим
Y0 = g0 + jwC0
=
=
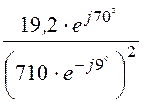= 38,1×10 –6×e j88° = (1,33 + j38,08)×10
–6 Cм/км.
Отсюда поперечные первичные параметры
g0 = Re(Y0) = 1,33×10 –6 Cм/км,
C0 =Im(Y0) =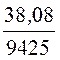
×10 –6 = 4,04×10 –9 Ф/км.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.