Электрические цепи с распределёнными параметрами в установившемся РЕЖИМЕ, страница 5

Сравнивая результаты расчётов двух однотипных линий разной длины (в задаче 8.8 длина линии 300 км,  в задаче 8.9 – 900 км), видим, что во втором случае резко выросли напряжение в конце линии и ток в начале линии в режиме холостого хода при значительном уменьшении тока в режиме короткого замыкания. Можно сделать вывод, что, начиная с некоторого значения длины линии, режим холостого хода в высоковольтной ЛРП оказывается опаснее режима короткого замыкания.

Задача8.10.  Для трёхфазной ЛЭП, согласованной с нагрузкой, известны комплексы фазного напряжения в начале линии U₁= 100 кВ и фазного тока в конце линии  i₂ = 190е ^–j90°A.  Определить КПД линии, если её характеристическое сопротивление  Z_C = 500е ^–j10° Ом.

Решение

Поскольку линия согласована с нагрузкой, сопротивление нагрузки равно характеристическому, и тогда напряжение в конце линии

U₂= i₂·Z_C = 0,19е ^–j90°·500е ^–j10° = 95е ^–j100°кВ.

Поскольку при согласованной нагрузке  U₂= U₁e ^-al, то

e ^-al = U₂/U₁ = 95/100 = 0,95.

КПД линии    h= e ^-2al =0,95²= 0,903.

8.1.3. Линии при согласованной нагрузке

Задача8.11.Двухпроводная линия длиной 100 км нагружена на повторное сопротивление Z_С = 410е ^-j30° Ом.

Напряжение на входе линии –  u₁(t) = 220sin(314t + 120°) В,  на выходе –  u₂(t) = 188,7sin(314t + 79,9°) В.  Определить ток и напряжение, записать их мгновенные значения в точке А  в 20 км от конца линии.

Решение

Повторным называют сопротивление нагрузки, равное волновому сопротивлению линии:   Z_Н = Z_С. Уравнения линии в согласованном режиме:

U₁ = U₂∙е ^γl = U₂∙е ^αl∙е ^jβl;

I₁ = I₂∙е ^γl = I₂∙е ^αl∙е ^jβl.

Для расчёта тока и напряжения в точке А необходимо знать параметры линии: коэффициент затухания α и коэффициент фазы β. Находим их из первого уравнения линии:

е ^γl = U₁/U ₂ = 220е ^j120°/188,7е ^j79,9° = 1,166е ^{j40,1° = +j0,7 рад};

е ^αl = 1,166;    αl = lп1,166 = 0,153;    α = 0,00153 Нп/км;    βl = 0,7 + 2pk рад.

β_op ==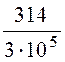» 10 ^-3 рад/км;       β_opl » 0,1 рад;

таким образом,  k = 0   и     β = 0,007 рад/км.

Тогда напряжение в точке А: 

U_А = U₂∙е ^γl = 188,7е ^j79,9°·е ^0,00153∙20∙е ^j0,007∙20 =

= 194,6е ^j79,9°∙е ^{j0,14 рад = 8,02°} = 194,6е ^j87,92° В.

Соотношение  Z_вх = Z_С справедливо для любого сечения линии, поэтому ток в точке А можно вычислить как

I_А  = U_А/Z_С = 194,6е ^j87,92°/(410е ^-j30°) = 0,475е ^j117,92° А.

Мгновенные значения напряжения и тока:

u_А(t) = 194,6sin(314t + 87,92°) В,         i_А (t) = 0,475sin(314t + 117,92°) А.

Задача8.12. Линия длиной 25 км получает питание от источника ЭДС е₁ = 141,4sin5000t В  с внутренним сопротивлением  r_вн =100 Ом. Параметры линии:  Z_С = 335,5 – j497,4 Ом,  γ = (3,48 + j19,70)∙10 ^-3 1/км,  Z_Н = Z_С.  Определить токи, напряжения, мощности на входе и в конце линии, найти КПД линии.

Ответы: U₁ = 90,6 В,       I₁ = 0,151 А,    Р₁ = 7,65 Вт;

U₂ = 83,04 В,     I₂ = 0,138 А,    Р₂ = 6,43 Вт;    η = 0,84.

Задача8.13. Двухпроводная линия длиной 100 км нагружена на сопротивление   Z_С = 1410е ^-j30° Ом.  В 20 км от конца линии напряжение u_а(t) = = 141,4sin(314t + 60°) В.  В точке  “b”, находящейся в 40 км от её конца известен ток   i(t) = 0,164sin(314t + 120°) А.

Определить мгновенное и действующее значения напряжения на входе линии.

Ответ:  u₁(t) = 715,6sin(314t + 180°) В;   U₁ = 715,6 В.

Задача8.14. Линия длиной   l = 20 км   и вторичными параметрами  Z_С = 1350е ^-j24° Ом  и  γ = 0,0175 + j0,039 1/км  нагружена на сопротивление, равное волновому. Определить мощность Р₂, передаваемую в нагрузку, и мощность Р₁, подводимую к линии, если напряжение  U₁ = 10 В.

Ответы:   Р₁ = 67,67 мВт,    Р₂ = 33,6 мВт.

Задача 8.15. Воздушная линия связи имеет следующие параметры:

r₀ = 2,84 Ом/км,   g₀ = 0,7 мкСм/км,   L₀ = 1,94 мГн/км,   C₀ =  6,25 нФ/км.