Электрические цепи с распределёнными параметрами в установившемся РЕЖИМЕ, страница 3

Вторичные параметры:

- характеристическое сопротивление   Z_C = 710×e ^–j9° Ом,

- коэффициент распространения

g === 27,1×10^-3×e ^j79° = (5,16 + j26,55)×10^-3 1/км.

Отсюда коэффициент затухания –  a = Re(g) = 5,16×10 ^–3 Нп/км,  

коэффициент фазы –  b = Im(g) = 26,55×10 ^–3 рад/км.

Вычисляем гиперболические функции:     gl = 0,722 + j3,717;

e^gl = 2,059×e ^j213° = -1,727 – j1,121;           e^–gl = 0,486×e ^–j213° = -0,407 + j0,265;

sh gl = ½[e^gl – e^–gl] = -0,660 – j0,693 = 0,957×e ^-j133,6°;

ch gl = ½[e^gl + e^–gl] = -1,067 – j0,428 = 1,150×e ^-j158,1°;

th gl = sh gl/ch gl = 0,832×e ^j24,5°.

Сопротивления холостого хода и короткого замыкания:

Z_1X = Z_C /th gl = 710×e ^–j9°/(0,832×e ^j24,5°) = 854×e ^–j33,5° Ом,

Z_1К= Z_C th gl = 710×e ^–j9°×0,832×e ^j24,5° = 591×e ^j15,5° Ом.

ЗАДАЧА 8.4. Для двухпроводной воздушной линии связи известны вторичные параметры на частоте 50 Гц:

Z_C = 440×e ^–j10° Ом,       g = (4 + j18)×10 ^–3 1/км.

Эта линия работает на постоянном токе и питает нагрузку  r_Н = 400 Ом. Напряжение на входе линии   u₁ = 600 В. Определить  u₂  и  I₁, если длина линии  l = 200 км.

Решение

Определим первичные параметры линии  r₀и  g₀, которые при работе линии на постоянном токе останутся теми же:

r₀= Re(g ·Z_C) = Re(18,44·10 ^-3·e ^j77,5°·440·e ^–j10°) = 3,105 Ом/км,

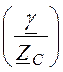g₀= Re= Re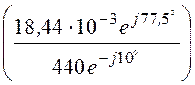= 1,826·10 ^-6 Cм/км.

Вторичные параметры линии при работе на постоянном токе:

Z_C =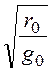==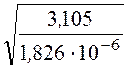 1303 Ом,

g === 2,382·10 ^-3 1/км.

Напряжение в конце линии и ток в начале линии найдём, используя основные уравнения длинной линии в гиперболических функциях с учётом того, что  I₂ = u₂/r_Н:

u₁ = u₂·ch gl + I₂Z_C·sh gl = u₂·ch gl +Z_C·sh gl = u₂·(ch gl +sh gl), отсюда искомое напряжение

u₂ =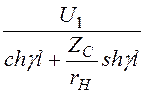==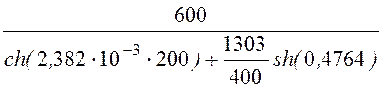 220 В.

Ток в начале линии

I₁ =·shgl + I₂·chgl =·shgl + ·chgl =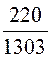·0,4945 +·1,116 = 0,697 А.

Задача8.5. Телефонная линия длиной 25 км на частоте 800 Гц обладает параметрами: Z_С = 366,2е ^-j40,58° Ом,  γ = (36,15 + j41,75)∙10 ^-3 1/км. Определить напряжение, ток и мощность сигнала на входе линии, если линия подключается к источнику постоянного тока при  r_н = 1500 Ом  и токе  I₂ = 50 мА.

Ответы:  U₁ = 100,4 В,   I₁ = 51,75 мА,   Р₁= 5,196 Вт.

Задача8.6. Определить сопротивления Т- и П-схем замещения ЛРП длиной  l = 400 км с параметрами:

Z_С = 391е ^-j3,75° Ом   и   γ = (0,187 + j1,058)∙10 ^-3 1/км.

Ответы:   сопротивления  Т-схемы  замещения (рис. 8.1,а):   Z_1Т = Z_2Т = = 20,74 + j82,69 Ом,     Z_0Т = 92,4 – j932,1 Ом;  сопротивления П-схемы замещения (рис. 8.1,б):     Z_1П = Z_2П = 206 – j1781 Ом,   Z_0П = 37,1 + j158,9 Ом.

ЗАДАЧА 8.7.  Трёхфазная сталеалюминиевая воздушная линия электропередачи длиной 300 км имеет следующие параметры (на фазу):

r₀ = 0,08 Ом/км,  g₀ = 3,75×10 ^–8 Cм/км,  wL₀ = 0,42 Ом/км,  wC₀ = 2,7 мкСм/км.

Вычислить вторичные параметры линии, фазовую скорость и длину волны.

Найти фазное напряжение, ток и активную мощность в начале линии, КПД, если на приёмном конце линейное напряжение 330 кВ, активная мощность 300 МВт и коэффициент мощности нагрузки равен 0,92.

Вычислить комплексы напряжения падающей и отражённой волн в начале и в конце ЛЭП.

Решение

Предполагаем, что нагрузка линии симметрична, соединена звездой. Поэтому расчет выполним для одной фазы.

Рассчитаем вторичные параметры линии:

- характеристическое сопротивление

Z_C =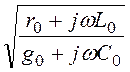==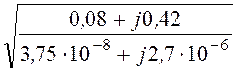= 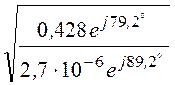398×e ^–j5° Ом,

- коэффициент распространения

g ===

= 1,07×10 ^–3×e ^j84,2° = (0,108 + j1,069)×10 ^–3 1/км.

Отсюда коэффициент затухания –  a = Re(g) = 0,108×10 ^–3 Нп/км,  

коэффициент фазы –  b = Im(g) = 1,069×10 ^–3 рад/км.

Фазовая скорость и длина волны:

v ===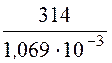 294 000 км/с;λ ===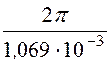 5880 км.

Вычисляем гиперболические функции:     gl = 0,033 + j0,321;

e^gl = 1,033×e ^j18,4° = 0,980 + j0,326;           e^–gl = 0,968×e ^-j18,4° = 0,919 – j0,305;