Электрические цепи с распределёнными параметрами в установившемся РЕЖИМЕ, страница 4

sh gl = ½[e^gl – e^–gl] = 0,031 + j0,316 = 0,317×e ^j84,4°;

ch gl = ½[e^gl + e^–gl] = 0,949 + j0,01 = 0,950×e ^j0,62°.

Получим комплексы фазных напряжения и тока в конце линии:

u_2Ф =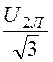== 190,5 кВ;    cosj ₂ = 0,92, поэтому  j ₂ = 23,1°;

I_2Ф =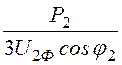==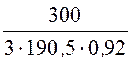 0,571 кА;   y_i2 = y_u2 – j ₂ = -j ₂;

I_2Ф = I_2Ф·e ^-jj2 = 0,571×e ^–j23,1°кА.

По основным уравнениям длинной линии в гиперболических функциях (8.4) рассчитаем комплексы фазных напряжения и тока в начале линии:

u_1Ф = u_2Ф·ch gl + I_2ФZ_C·sh gl =

= 190,5·0,95×e ^j0,62° + 0,571×e ^–j23,1°·398×e ^–j5°·0,317×e ^j84,4° = 229,3·e ^j15,6° кВ;

I_1Ф =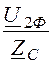·sh gl + I_2Ф·ch gl =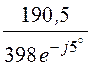·0,317×e ^j84,4° + 0,571×e ^–j23,1°·0,95×e ^j0,62° =

= 0,505×e ^-j6,3° кА.

Активная мощность в начале линии

Р₁ = 3Re(u_1Ф·) = 3·229,3·0,505·cos(15,6° + 6,3°) = 322 МВт.

Коэффициент полезного действия линии

h= Р₂/Р₁ = 300/322 = 0,93.

Электромагнитные процессы в длинной линии рассматриваются как результат наложения падающей (прямой) и отражённой (обратной) волн –

u= u_отр + u_пад = А₁e ^gх + А₂e ^-gх,

I= -I_отр + I_пад = -e ^gх + e ^-gх, где А₁ и А₂ – постоянные интегрирования, которые определяются, например, через напряжение и ток в конце линии:

А₁ =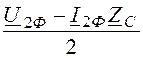e ^-gl =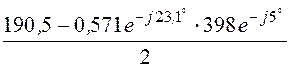·0,968×e ^-j18,4° = 51,9×e ^j76,8°;

А₂ =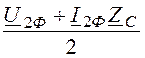e ^gl =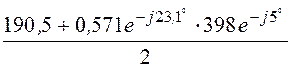·1,033×e ^j18,4° = 209,3×e ^j3,1°.

В начале линии  х = 0, поэтому

u_пад(х = 0) = А₂= 209,3×e ^j3,1° кВ,       u_отр(х = 0) = А₁= 51,9×e ^j76,8° кВ,

I_пад(х = 0) = u_пад(х = 0)/Z_C = 0,526×e ^j8,1° кA,

I_отр(х = 0) = u_отр(х = 0)/Z_C = 0,13×e ^j81,8° кA.

В конце линии  х = l,  поэтому

u_пад(х = l) = А₂·e ^-gl =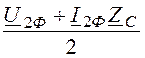= 202,6×e ^–j15,3° кВ,

u_отр(х = l) = А₁·e ^gl =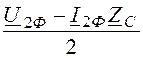= 53,6×e ^j95,2° кВ,

I_пад(х = l) = u_пад(х = l)/Z_C = 0,509×e ^–j10,3° кA,

I_отр(х = l) = u_отр(х = l)/Z_C = 0,135×e ^j100,2° кA.

Как и следовало ожидать, из-за потерь в линии падающая волна уменьшается к концу линии, а отражённая волна затухает в направлении от конца линии к началу.

ЗАДАЧА 8.8. В конце линии задачи 8.7 произошло: а) отключение нагрузки; б) трёхфазное короткое замыкание. Для каждого случая определить линейные напряжения и токи в начале и в конце линии, если фазное напряжение на входе осталось таким, как рассчитано в задаче 8.7.

Определить также значения напряжения и тока падающей и отражённой волн в конце линии.

Решение

При решении задачи воспользуемся основными уравнениями длинной линии в гиперболических функциях (8.4).

а) при отключении нагрузки (режим холостого хода) ток в конце линии

I_2Ф = 0, поэтому

u_2Ф =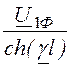==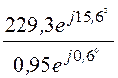 241×e ^j15° кВ,        u_2Л =u_2Ф =·241 = 418 кВ;

I_1Ф =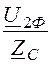sh gl =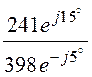·0,317×e ^j84,4° = 0,192×e ^j104,4° кА,      I_1Л = I_1Ф = 0,192 кА.

В режиме холостого хода коэффициент отражения +1, то есть падающая волна отражается полностью, причём без изменения знака. Поэтому

u_пад(х = l) = u_отр(х = l). С учётом этого

u_2Ф = u_пад(х = l) + u_отр(х = l) = 2u_пад(х = l) = 241×e ^j15° кВ, откуда  u_пад(х = l) = u_отр(х = l) = u_2Ф/2 = 120,5×e ^j15° кВ,

I_пад(х = l) = I_отр(х = l) = u_пад(х = l)/Z_C = 0,303×e ^j10° кА.

б) при коротком замыкании напряжение в конце линии

u_2Ф = 0, поэтому

I_2Ф =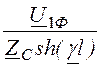==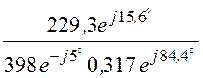 1,817×e ^–j63,8°кА,        I_2Л = I_2Ф = 1,817 кА;

I_1Ф = I_2Ф·сh gl = 1,817×e ^–j63,8°·0,95×e ^j0,6° = 1,726×e ^–j63,2° кА,      I_1Л = I_1Ф = 1,726 кА.

В режиме короткого замыкания коэффициент отражения равен -1. Поэтому I_пад(х = l) = -I_отр(х = l). С учётом этого

I_2Ф = I_пад(х = l) – I_отр(х = l) = 2I_пад(х = l) = 1,817×e ^–j63,8° кА, откуда  I_пад(х = l) = -I_отр(х = l) = I_2Ф/2 = 0,909×e ^–j63,8° кА,

u_пад(х = l) = -u_отр(х = l) = I_пад(х = l)·Z_C = 362×e ^–j58,8° кВ.

Задача8.9. В режимах а) холостого хода и б) короткого замыкания определить линейные напряжения и токи в начале и в конце линии задачи 8.8, если её длина 900 км, а фазное напряжение на входе u_1Ф = 229,3 кВ.

Ответы:  сhgl = 0,574 + j0,080,   shgl = 0,056 + j0,824;

а) u_2Л = 685 кВ;  I₁ = 821 А;    б) I₂ = 697 А;    I₁ = 404 А.