Электрические цепи с распределёнными параметрами в установившемся РЕЖИМЕ, страница 8

Ответы:   γ = jβ = j0,314 1/м,   L₀ = 2 мкГн/м,  С₀ = 5,55 пФ/м,

Р₁ = 48 Вт,   η = 1.

Задача8.26. Определить ток генератора, питающего нагруженную линию без потерь при напряжении  U_ген = 120 В  и следующих параметрах линии:  l = 100 м,   λ = 60 м,  L₀ = 5,3 мкГн/м,   r_н = 380 Ом.

Ответы:   Z_С = 1590 Ом,  β = 0,1047 рад/м,   Z_ВХ = 255,6е ^j59,69° Ом,

I₁ = 0,047е ^-j59,69° А.

Задача 8.27. В конце воздушной линии без потерь длиной  l = 12 м включена индуктивность  l = 17,3 мкГн. Определить, на каком расстоянии от конца линии находится ближайшая пучность напряжения и тока, если частота источника  ω = 10⁸ рад/с и параметры линии  L₀ = 10 мкГн/м,  C₀ = 1,11 пФ/м.

Решение

Индуктивность l можно смоделировать отрезком короткозамкнутой ЛБП длиной l₁. Рассчитаем длину отрезка.

Сопротивление индуктивности в комплексной форме  jωL, входное сопротивление короткозамкнутой ЛБП   Z_К = jZ_C tg(βl₁), то есть ωL= Z_C tg(βl₁), где вторичные параметры линии  Z_C =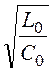==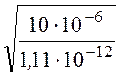 3000 Ом,

β = ω= 10 ⁸= 0,333 рад/м.

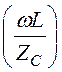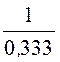Получаем:   l₁ =arctg=arctg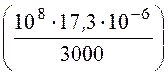= м.

Длина волны   λ ===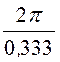 6p  м.

У короткозамкнутой ЛБП ближайшая пучность напряжения находится от конца линии на расстоянии, равном четверти длины волны:   ¼λ = 1,5p  м.

У данной линии с учётом отрезка l₁:   1,5p– l₁ = 1,5p– 0,5p=p = 3,14 м.

Пучность тока смещена по сравнению с пучностью напряжения на четверть длины волны. Поэтому координата пучности тока следующая:

p + 1,5p= 2,5p= 7,85 м.

Задача 8.28. Для согласования рабочей линии с нагрузкой на частоте 100 МГц необходимо индуктивное сопротивление 800 Ом, которое может быть смоделировано отрезком линии без потерь. Определить наименьшую длину отрезка короткозамкнутой линии без потерь, выполненной из медных проводов радиусом  r= 2 мм  с расстоянием между проводами  d= 20 см. Рассчитать сопротивление отрезка при разомкнутом конце.

Указание. Первичные параметры ЛБП вычислить по формулам:

L₀ =ln= 4·10 ^-7·ln Гн/м;      С₀ =.

Ответ:  у_min = 46,1 см,   Z_ХХ = -j381,9 Ом.

Задача 8.29. Линия без потерь с параметрами: l = 30 м,   f = 15 МГц,  Z_С = 600 Ом работает на нагрузку:  U₂ = 120 В, r_н = 300 Ом. Определить положение минимумов и максимумов напряжения вдоль линии.

Решение

Известно, что в режиме холостого хода или при коротком замыкании в линиях без потерь возникают стоячие волны. Поскольку при этом коэффициент отражения K = ±1, прямая и обратная волны одинаковы по величине, их наложение даёт нули и пучности напряжения, распределенные по линии при ХХ (КЗ) в соответствии с выражениями:

у_{узлов(пучностей)} = (2k+ 1)∙λ/4;       у_{пучностей(узлов)} = kλ/2;      k= 0, 1, 2, ...

При произвольной несогласованной нагрузке  |K| < 1, прямая и обратная волны не равны между собой. В результате наложения этих волн в линии возникают минимумы и максимумы напряжения. Очевидно, что они будут в тех точках, где прямая и обратная волны либо совпадают по фазе (максимумы), либо отличаются на 180° (минимумы).

1. Определим коэффициент отражения Kволны от нагрузки и оценим напряжения прямой и обратной волн  U_пр, U_обр.

K = 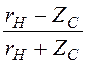=  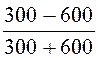= -0,333,    то есть    U_обр = -0,333U_пр.

В конце линии напряжение находится как 

U₂ = U_пр + U_обр = U_пр – 0,333·U_пр = 0,667·U_пр = 120 В.

Поскольку  K< 0,  то в конце линии имеет место минимум напряжения, то есть  U_min = 120 В,  причём:

U_пр = U_min/0,667 = 180 В,    U_обр = -0,333U_пр = -60 В.

Максимальное же значение напряжения     U_mах = 180 + 60 = 240 В.

2. Итак, первый минимум напряжения находится в конце линии. Далее минимумы напряжения следуют через  λ/2. Оценим длину волны:

λ === 300∙10³/(15∙10⁶) = 20 м.

Максимумы напряжения сдвинуты относительно минимумов на   λ/4 = = 5 м  и далее по линии также идут через  λ/2.