Тогда ток утечки через изоляцию кабеля на длине в 1 км составит
I = g0lU = 0,0628∙10 -6∙1000∙10∙10 3 = 0,628 А.
Мощность тепловых потерь в изоляции Р = U∙I = 10000∙0,628 = 6280 Вт.
Задача 13.8. Однослойный коаксиальный кабель работает под напряжением 600 В и имеет размеры: r1 = 4 мм, r2 = 8 мм, l = 10 км, удельная проводимость изоляции g = 1∙10 -9 См/м. Определить ток утечки и его плотность в изоляции на поверхности жилы и на внутренней стороне оболочки кабеля, а также тепловые потери кабеля.
Ответы: I = 54,4 мА, d1 = 216 мкА/м2, d2 = 108 мкА/м2, Р = 32,6 Вт.
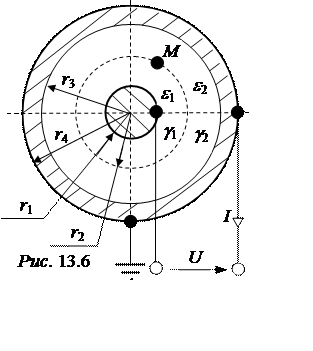 Задача 13.9. Рассчитать ток утечки между двумя жилами
коаксиального кабеля (рис. 13.6). Изоляция выполнена двухслой-ной из
несовершенного диэлектрика (удельные проводимости g1 = 5·10-8
См/м и g2 = 2·10 -8 См/м,
относительные диэлектриче-ские проницаемости e1 = 2 и e2 = 5). Напря-жение U
= 10 кВ. Геометрические размеры – r1 = 1 мм, r2 = 2 мм, r3 = 3 мм.
Задача 13.9. Рассчитать ток утечки между двумя жилами
коаксиального кабеля (рис. 13.6). Изоляция выполнена двухслой-ной из
несовершенного диэлектрика (удельные проводимости g1 = 5·10-8
См/м и g2 = 2·10 -8 См/м,
относительные диэлектриче-ские проницаемости e1 = 2 и e2 = 5). Напря-жение U
= 10 кВ. Геометрические размеры – r1 = 1 мм, r2 = 2 мм, r3 = 3 мм.
Найти удельные тепловые потери в окрестности точки М, проводимости и ёмкости между телами, построить схему замещения системы. Кабель считать весьма протяжённым, а расчеты выполнить на единицу длины.
Дополнительно определить предельно возможную длину кабеля как линии электропередачи.
Решение
1. Пусть ток утечки равен i. Тогда в соответствии с формулами (13.2) плотность тока, напряжённость и потенциал в слоях диэлектрика определяются по формулам
d = i/(2prl); Е1 =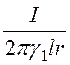 , Е2
=
, Е2
=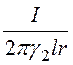 ; j1 =
; j1 =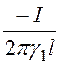 lnr+ А1,
j2 =
lnr+ А1,
j2 =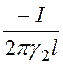 lnr + А2.
lnr + А2.
2. Напряжение, приложенное к устройству,
U = j 1(r1) – j 1(r2) + j 2(r2) – j 2(r3) =
=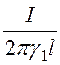 ln
ln![]() +
+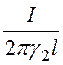 ln
ln![]() =
=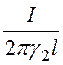 ln
ln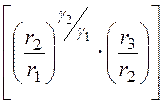 .
.
3. Отсюда ток утечки на единицу длины
i0 =![]()
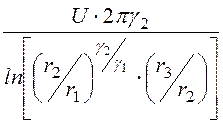 =
=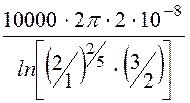 = 1,841·10-3 А/м
= 1,841 мА/м.
= 1,841·10-3 А/м
= 1,841 мА/м.
4. Проводимость кабеля токам утечки найдём по закону Ома:
g0 = I0/U = 1,841·10-3/104 = 0,1841·10-6 Cм/м = 0,1841 мкСм/м.
5. Этот же ответ можно получить, используя аналогию
между электрическим полем в проводящей среде и электростатическим. Формула
ёмкости однослойного коаксиального кабеля (13.3): C0 =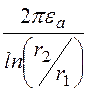 .
.
 ёмкости слоёв и всего данного кабеля:
ёмкости слоёв и всего данного кабеля:
C10
=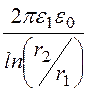 =
=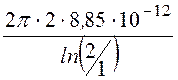 = 160,4 пФ/м;
= 160,4 пФ/м;
C20
=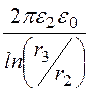 =
=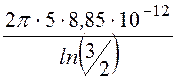 = 873,5 пФ/м;
= 873,5 пФ/м;
так как ёмкости соединены последовательно, то
C0 =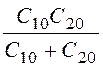 =
=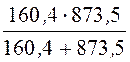 = 135,5 пФ/м.
= 135,5 пФ/м.
Проводимости слоёв и всего кабеля на единицу длины:
g10 =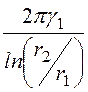 =
=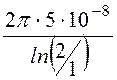 = 0,454·10-6 Cм/м;
= 0,454·10-6 Cм/м;
g20 =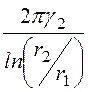 =
=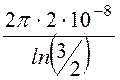 = 0,310·10-6 Cм/м;
= 0,310·10-6 Cм/м;
g0 =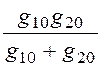 =
=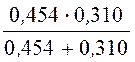 = 0,1842 мкСм/м.
= 0,1842 мкСм/м.
6. Электрическая схема замещения устройства показана на рис. 13.7.
7. Плотность тока в окрестности точки М:
d = i0/(2pr2) = 1,841·10-3/(2p ·2·10-3) = 0,147 А/м2;
тепловые потери в окрестности точки М по закону Джоуля-Ленца:
p1 = d 2/g1 = 0,1472/(5·10-8) = 0,432·106 Вт/м3 = 0,432 МВт/м3;
p2 = d 2/g2 = 0,1472/(2·10-8) = 1,08·106 Вт/м3 = 1,08 МВт/м3.
8. Сечение внутренней жилы кабеля меньше, чем наружной, и рав-но S = pr12 = 3,14 мм2. Если принять, что жилы алюминиевые, а допустимая плотность тока 1 А/мм2, то допустимый ток для кабеля будет равен 3,14 А. Тогда допустимая длина кабеля (пока он ещё хоть сколько-нибудь способен питать нагрузку, а не целиком себя) –
lдоп = 3,14/i0 = 3,14·1000/1,841 = 1705 м.
А для получения приемлемого КПД эта длина должна быть ещё меньше.
Задача 13.10. Цилиндрический конденсатор с двухслойной изоляцией (рис. 13.6) работает при напряжении U = 10 кВ. Известны размеры конденсатора (r1 = 0,08 см, r2 = 0,2 см, r3 = 0,6 см, l = 5 см) и свойства изоляции (g1 = 1∙10 -8 См/см, e1 = 2, g2 = 4∙10 -8 См/см, e2 = 6). Рассчитать ток утечки через изоляцию конденсатора, найти выражения удельной проводимости g0 и ёмкости С0 конденсатора.
Ответы: I = 2,634 мА,
g0 =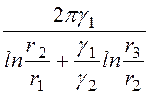 = 5,273∙10 -8
См/м, С0 =
= 5,273∙10 -8
См/м, С0 =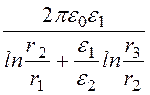 =
43,34 пФ/м.
=
43,34 пФ/м.
Задача 13.11. Плоский конденсатор ёмкостью 10 мкФ находится под напряжением 1 кВ. Диэлектрическая проницаемость изоляции e = 4, а удель-ная проводимость g = 1∙10 -12 См/м. Определить ток утечки между обклад-ками конденсатора.
Методические указания: из формулы ёмкости С = q/U = e0e S/d можно найти соотношение S/d = С/(e0e), которое затем использовать в аналогичной формуле проводимости конденсатора: g = g ·С/(e0e).
Ответ: I = 0,283 мА.
Задача 13.12. Два плоских конденсатора С1 = 0,2 мкФ, С2 = 0,5 мкФ с несовершенными диэлектриками соединены последовательно и подключа-ются к источнику напряжения U = 1200 В. Диэлектрические проницаемости диэлектриков: e1 = 2,4, e2 = 4; удельные проводимости: g1 = 0,2∙10 -9 См/м, g2 = 5∙10 -9 См/м. Определить напряжения на каждом из конденсаторов в момент включения, а также в установившемся режиме.
Решение
При решении задачи воспользуемся схемой замещения системы, представленной на рис. 13.7. В момент включения весь ток проходит по незаряженным конденсаторам в соответствии со вторым законом комму-тации. То есть через конденсаторы проходит один и тот же заряд
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.