чивающую силу I3W3.
Методические указания к решению задачи. По методу двух узлов рекомендуется рассчитать и построить зависимости Ф1(UмАВ) и Ф2(UмАВ), точка их пересечения определит величину UмАВ, а также Ф1 и Ф2, затем с помощью второго закона Кирхгофа можно найти I3W3 (см. рис. 2.34).
UмАВ= I1W1 – Н1×l1 – НВ×lВ, UмАВ= -I2W2 – Н2×l2, I3W3 = UмАВ – Н3×l3.
Ответы: Ф1 = Ф2 = -15,5×10-4 Вб, UмАВ = 690 А, Ф3 = -31×10-4 Вб, I3W3 = 2140 А.
3. ЛИНЕЙНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
3.1. Основные теоретические положения
Синусоидальным называется ток, изменяющийся во времени по синусоидальному закону. Значение тока в некоторый момент времени называется его мгновенным значением и обозначается малой буквой i. Ток считается определённым, если известен закон изменения его мгновенного значения и указано положительное направление. Для синусоидального тока
i(t) = Im×sin(wt+ y ), где: Im – максимальное значение или амплитуда тока;
= 2p/Т = 2pf– угловая частота;
T и f – период и частота тока;
y – начальная фаза.
Кроме амплитудного значения, он характеризуется еще и
средним Iср = 2Im /p, а также
действующим I = Im/![]() значениями.
значениями.
Пассивными элементами цепи синусоидального тока являются активное сопротивление R (учитывает преобразование электрической энергии в другие виды), индуктивность L (учитывает наличие магнитного поля и явление самоиндукции) и ёмкость C (учитывает наличие электрического поля). Состояние этих элементов при подключении их к напряжению u = Um×sinwt характеризуется данными табл. 3.1.
Таблица 3.1
Элемент |
Мгновенное значение тока |
Закон Ома для действующих значений |
|
|
R |
|
|
|
|
L |
|
|
|
|
C |
|
|
Основные величины, имеющие место в цепи с последовательным соединением R, Lи C, если к ней подведено напряжение u = Um×sinωt, приведены в табл. 3.2.
При xL = xC, чего можно добиться, изменяя L, С или ω, в цепи R, L, С
возникает резонанс напряжений, и тогда UL = UС , UR = U, j = 0 (cosj =1), ток I = U/Rимеет максимальное значение.
Таблица 3.2
Цепь |
Мгновенное значение тока |
Закон Ома для действующих значений |
Векторная диаграмма при xL>xC |
|
|
i = Z = j =arctg |
I = |
|
Если в цепи последовательно соединено по несколько R,
L и С, то её полное
сопротивление Z =![]() , а
угол сдвига фаз напряжения и тока j= arctg
, а
угол сдвига фаз напряжения и тока j= arctg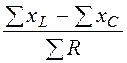 .
.
При параллельном соединении ветвей, в каждой из которых может быть включена любая комбинация R,
L и С, токи раскладываются на активные
(совпадающие с напряжением) и реактивные (перпендикулярные напряжению)
составляющие. Для тока k-ой ветви Ikа= Ik×cosj k , Ikр =
Ik×sinj k , Ik =![]() . Активная и реактивная составляющие тока в
неразветвлённой части цепи, соответственно: Iа=SIkа ,Iр=SIkр .
. Активная и реактивная составляющие тока в
неразветвлённой части цепи, соответственно: Iа=SIkа ,Iр=SIkр .
При расчёте параллельного соединения часто пользуются проводимос-тями ветвей. Активная, реактивная и полная проводимости k-ой ветви:
gk =![]() =
=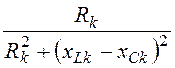 ;bk =
;bk =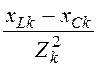 =
=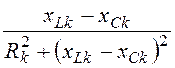 ;yk =
;yk =![]() .
.
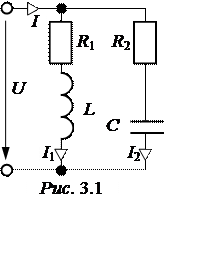 В схеме параллельного резонансного контура с потерями
(рис. 3.1) при bL = bC или
В схеме параллельного резонансного контура с потерями
(рис. 3.1) при bL = bC или 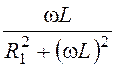 =
=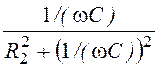 возникает резонанс
токов. При этом I1р =
I2р,
j = 0 (cosj =1) и ток в нераз-ветвлённой части цепи имеет
минимальное значение, если R1 и R2 меньше
возникает резонанс
токов. При этом I1р =
I2р,
j = 0 (cosj =1) и ток в нераз-ветвлённой части цепи имеет
минимальное значение, если R1 и R2 меньше 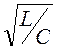 .
.
В схеме смешанного соединения, используя проводимости параллельно включенных ветвей, можно заменить их одной эквивалентной ветвью. После этого цепь будет представлять собой последовательное соединение, расчёт которого освещён выше.
При синусоидальном токе различают следующие мощности:
- мгновенную p(t) = u(t)×i(t),
- активную (среднее за период значение мгновенной мощности)
P = U×I×cosj= U×Iа = Uа×I = I 2×R = U 2×g,
- реактивную Q = U×I×sinj = ±U×Iр= ±Uр×I = ±I 2×x = ±U 2×b,
(здесь и далее в формулах верхний знак берётся в случае индуктивного характера нагрузки и нижний – в случае ёмкостного характера),
- полную S = U×I = I 2×Z = U 2×y.
В электроэнергетике большое значение имеет коэффициент мощности P/S = cosj. При его повышении возрастает эффективность использования оборудования и экономится электроэнергия. Для повышения используется обычно резонанс токов, а именно: параллельно нагрузке, которая носит, как правило, индуктивный характер, подключаются батареи статических конденсаторов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.