Линейные цепи синусоидального тока. Основные теоретические положения, страница 2

Широкое распространение для расчёта цепей синусоидального тока получил комплексный (символический) метод, основанный на использовании теории комплексных чисел. Связь между синусоидальной величиной v(t)=V_m×sin(ωt+ψ) и комплексами: v=Im[V_m×e^j(ωt+ψ)]=Im[V_m×e^jωt×e^jψ]=Im[V_m×e^jωt], то есть (v¸V). Законы Ома и Кирхгофа в комплексной форме имеют точно та-кой же вид, как и при постоянном токе, нужно только использовать комплек-сы ЭДС, напряжений, токов и сопротивлений. В связи с этим цепи синусои-дального тока можно рассчитывать всеми методами, основанными на законах Ома и Кирхгофа и рассмотренными в разделе «Цепи постоянного тока».

Для любой ветви комплексное сопротивление

Z = R + j(x_L – x_C) = R± jx = Z×e ^jj.

Используется и комплексная проводимость ветви Y= 1/Z= y×e^-jj= gjb.

Комплексная мощность    S = P + jQ = U×,    то есть   P = Re[U×],   а  Q = Im[U×].   В цепях синусоидального тока имеет место баланс не только активных мощностей, но ещё и реактивных.

Явление наведения ЭДС в одном контуре или катушке при изменении тока в другом контуре или катушке называется явлением взаимной индукции, а возникающая ЭДС е_М – ЭДС взаимоиндуции. В расчётах чаще используется напряжение, компенсирующее эту ЭДС:  u_М = -е_М.  Напряжение взаимной ин-дукции на k-ом элементе   U_Мk = jwM_kl×I_l = jx_Mkl×I_l = Z_Mkl×I_l.  При составлении уравнений по второму закону Кирхгофа знак напряжения определяется в со-ответствии со следующим правилом знаков: если направление обхода одной катушки и ток другой катушки относительно одноимённых зажимов совпада-ют, напряжение взаимоиндукции берётся с «плюсом», иначе – с «минусом».

При последовательном соединении двух индуктивно связанных элементов возможны их согласное и встречное включения. При согласном включении (в обоих элементах ток направлен одинаково относительно одноимённых зажимов) полное сопротивление цепи  Z_согл = R + j(x+ 2x_М),  а при встречном –   Z_встр = R + j(x – 2x_М).

Сложные цепи при наличии взаимной индуктивности рассчитываются путём решения уравнений, составленных по законам Кирхгофа, или методом контурных токов, причём явление взаимной индукции учитывается через напряжение U_Мk как указано выше. Применение метода эквивалентного гене-ратора возможно только в случае, если искомая ветвь не имеет индуктивной связи с ветвями двухполюсника. Остальные методы неприменимы.

При наличии общего узла у двух индуктивно связанных элементов часто применяется развязка индуктивной связи (замена исходной схемы эквивалентной, не содержащей индуктивной связи). Если к общему узлу элементы подключены одноимёнными зажимами, то к сопротивлениям элементов добавляется по  –Z_М, а в общую ветвь включается +Z_М. Когда к общему узлу элементы подключены разноимёнными зажимами, знаки добавляемых сопротивлений меняются на противоположные.

Если токи в индуктивно связанных элементах   I₁ = I₁×e^jψ1  и  I₂ = I₂×e^jψ2 направлены относительно одноимённых зажимов одинаково, то передаваемая через взаимную индуктивность активная мощность

Р_М1®2 = -Р_М2®1 = Re[U_М1×] = Re[jωM×I₂×] = wM×I₁×I₂×sin(y₁ – y₂).

Для измерения активной мощности всей цепи или её участка применяются ваттметры. Условное обозначение и схема включения ваттметра показаны на рис. 3.4, 3.5 (задачи 3.3, 3.4). По принципу действия ваттметра его показание определяется напряжением u_W на катушке напряжения и током токовой катушки  I_W:

P_W = u_W×I_W×cos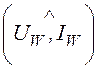= Re[U_W ×].

3.2. РАСЧЁТ ПРОСТЕЙШИХ ЦЕПЕЙ

3.2.1. Типовые примеры

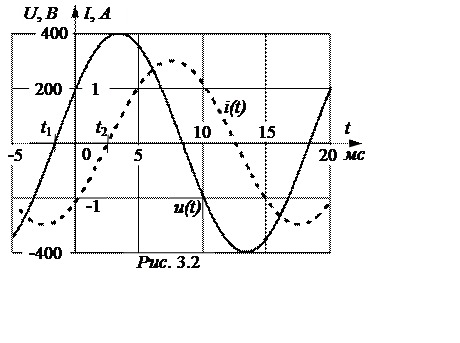
ЗАДАЧА 3.1. На рис. 3.2 приведены осциллограммы напряжения и тока. Требуется записать выражения для их мгновенных значений, определить действующие значения напряжения и тока.

Решение

По осциллограммам определяем период колебаний Т = 20 мс,  следовательно, час-тота  f =1/T = 50 Гц,  а угловая частота w = 2pf = 314 рад/с.  Начальные фазы напряжения и тока в градусах, соответственно:

ψ_u = -t₁×(360/T) = 1,67×(360/20) = 30°,    ψ_i = -t₂×(360/T) = -2,5×(360/20) = -45°,