Z23 = 10 + j10 Ом; Z = 20 + j10 Ом;
I1
= 4×e j18,4° A; I2
= 4![]() ×e –j26,6° A;
×e –j26,6° A;
 I3
= 4×e j108,4° A; PW = 160 Вт.
I3
= 4×e j108,4° A; PW = 160 Вт.
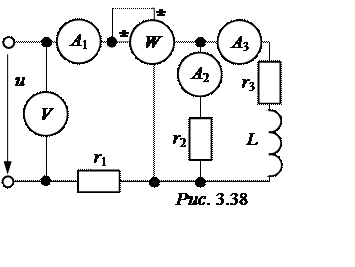
ЗАДАЧА 3.41. В схеме рис. 3.38 определить показания приборов, построить векторную диаграмму, проверить баланс мощностей. Задачу решить методами проводимостей и символическим. Известно:
u(t) =12![]() ×sin(100t +
90°) B,L = 0,12 Гн, r1 = 3 Ом,r2 = 10 Ом,r3 = 6 Ом.
×sin(100t +
90°) B,L = 0,12 Гн, r1 = 3 Ом,r2 = 10 Ом,r3 = 6 Ом.
Ответы:Z3 = 6![]() ×e j63,4° Ом;Z23 = 6 + j3
Ом;Z = 9 + j3 Ом;
×e j63,4° Ом;Z23 = 6 + j3
Ом;Z = 9 + j3 Ом;
I1
= 2×e j71,7° A; I2 =
0,6![]() ×e j98,1° A;
I3 = 1×e j34,7° A; PW = 24 Вт.
×e j98,1° A;
I3 = 1×e j34,7° A; PW = 24 Вт.
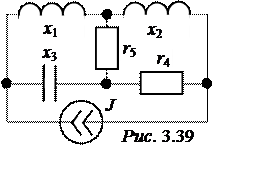
ЗАДАЧА 3.42. В схеме рис. 3.39 определить токи, построить топографическую диаграмму, совмещённую с векторной диаграммой токов, проверить баланс мощностей. Параметры цепи:
J = 10 A; х1 = х2 = х3 = r4 = 10 Ом;r5 = 5 Ом.
 Ответ: если по
вещественной оси напра-вить вектор тока источника, то
Ответ: если по
вещественной оси напра-вить вектор тока источника, то
I1 = -j30 A; I2 = -j10 A; I3 = 10 + j30 A;
I4 = 10 + j10 A; I5 = -j20 A.
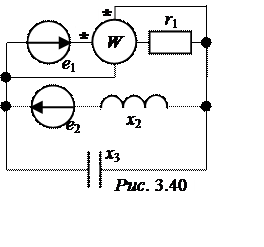
ЗАДАЧА 3.43. В схеме рис. 3.40 определить токи, построить топографическую диаграмму, совмещённую с векторной диаграм-мой токов, найти показание ваттметра и опре-делить его физический смысл. Параметры цепи:
e1(t) = 200![]() sinwtВ, e2(t)
= 200
sinwtВ, e2(t)
= 200![]() sin(wt – 90°) В; r1 = х2 = х3 = 20 Ом.
sin(wt – 90°) В; r1 = х2 = х3 = 20 Ом.
Ответы: I1 = -30 A; I2 = -10 – j20 A; I3 = j20 A; PW = -4000 Вт.
Ваттметр измеряет активную мощность, поступающую из первой ветви в остальные. Знак «минус» у мощности означает, что направление мощности обратное, то есть от остальных ветвей в первую.
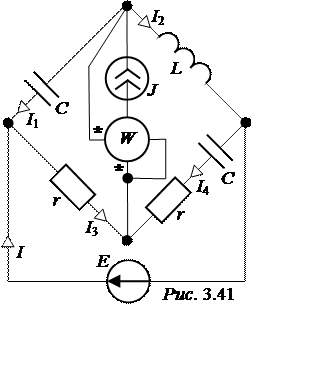
ЗАДАЧА 3.44.
Определить токи во всех ветвях и показание ваттметра в схеме рис. 3.41, если Е
= 100![]() В и она опережает J на 45° по фазе;
В и она опережает J на 45° по фазе;
J = 10 A; хL = r = 10 Ом; хC = 20 Ом.
 Ответ: если по
вещественной оси направить вектор J, то I = 7,5 + j12,5 A;
Ответ: если по
вещественной оси направить вектор J, то I = 7,5 + j12,5 A;
I1 = -j10 A; I2 = 10 + j10 A; I3 = 7,5 + j2,5 A; I4 = -2,5 + j2,5 A; PW = -1250 Вт.
3.4.3. Применение ПЭВМ для решения задач комплексным методом
ЗАДАЧА 3.45. Решить задачу 3.28 комплексным методом с помощью ПЭВМ.
Программа решения задачи в системе MathCAD.
u:= 200 r1 := 2 r2
:= 2 r3 := 4 r4 := 20 хC1
:= 8 хC2 := 8 хL := 6 j:=![]()
Определяем комплексные сопротивления ветвей
Z1 := r1 – j×хC1 Z2 := r2 + j×хL Z3 := r3 – j×хC2 Z4 := r4
Ze :=![]()
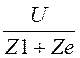 I2:=
I1×
I2:=
I1×I1 = 16+12.i I2 = 19.2-5.i I3 = -6.8+12.i I4 = 3.6+5.2i
Комплексная мощность источника
Si
:= U×![]() Si = 3.2´103 – 2.4i´103
Si = 3.2´103 – 2.4i´103
Активная и реактивная мощности приёмников
Pp := (|I1|)2×r1 + (|I2|)2×r2 + (|I3|)2×r3 + (|I4|)2×r4 Pp = 3.2´103
Qp := (|I1|)2×Im(Z1)+(|I2|)2×Im(Z2)+(|I3|)2×Im(Z3)+(|I4|)2×Im(Z4) Qp = -2.4´103
Следовательно, балансы мощностей сходятся.
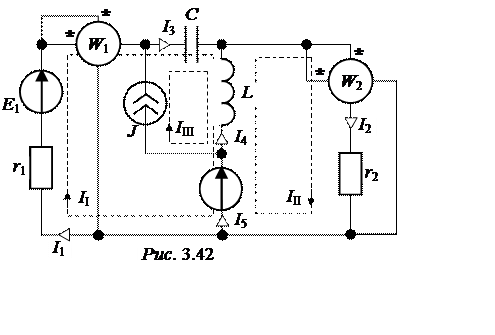
ЗАДАЧА 3.46. В схеме рис. 3.42 определить токи во всех ветвях и показания ваттметров, если Е1 = 380 В, Е2 = 220×е –j120° В, J = 10×е j120° A,
r1 = 10 Ом, r2= 20 Ом, L = 50 мГн, C = 150 мкФ.
Программа решения задачи в системе MathCAD.
j:=![]() Е1:= 380 Е2:= 220×е –j×120×deg J:=10×е j×120×deg
Е1:= 380 Е2:= 220×е –j×120×deg J:=10×е j×120×deg
r1 := 10 r2 := 20 L := 0.05 C := 15×10-5 ORIGIN := 1
Определим величины реактивных сопротивлений
w :=
100×p xL
:= w×L xC :=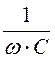 xL = 15.708 xC =
21.221
xL = 15.708 xC =
21.221
Расчёт токов произведём методом контурных токов (см. рис. 3.42) с учётом того, что третий контурный ток равен току источника J.
Матрицы контурных сопротивлений и контурных ЭДС
Rk :=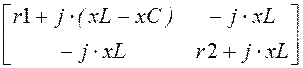 Ek :=
Ek :=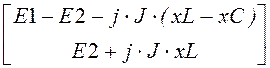
Контурные токи Ik := Rk -1×Ek Ik =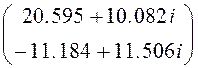
Токи ветвей
I1 := Ik1 I2 := Ik2 I3 := J + Ik1 I4 := -J – Ik1 + Ik2 I5 := -Ik1 + Ik2
I1 := 20.595 +10.082i I2 = -11.184+11.506i I3 := 15.595+18.742i
I4 := -26.779-7.237i I5 := -31.779+1.423i
Показания ваттметров
U1
:= E1 – I1×r1 P1 := Re(U1×![]() ) P1 = 2.568´103
) P1 = 2.568´103
U2 := I2×r2
P2 := Re(U2×![]() ) P2 = 5.149´103
) P2 = 5.149´103
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.