u= 380 B;r = 1 кОм; С = 2 мкФ.
Совместим вектор входного напряжения с вещественной осью. Тогда
U = U = 380 B.
Комплексное сопротивление цепи
Z = r
– jхС = r – j![]() = 1000 –
j
= 1000 –
j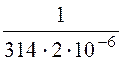 = 1000 – j1592 = 1880×e -j57,87° Ом.
= 1000 – j1592 = 1880×e -j57,87° Ом.
По закону Ома определяем комплекс тока в цепи
I =![]() =
=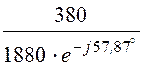 = 0,202×e j57,87° А.
= 0,202×e j57,87° А.
Комплекс напряжения на ёмкости
UС = I×(-jхС) = 0,202×e j57,87°×(-j1592) = 321,8×e –j32,13° В.
Мгновенное значение напряжения на ёмкости
uС(t) = Im![]() = 455,1×sin(wt – 32,13°) В.
= 455,1×sin(wt – 32,13°) В.
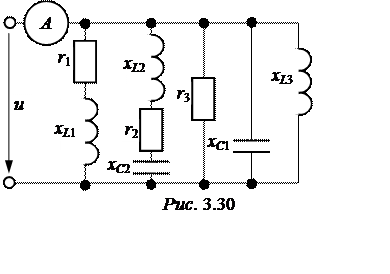
ЗАДАЧА 3.31. В схеме рис. 3.30 определить показание амперметра, если u(t) = 300×sin(wt – 30°) В;r1 = 12 Ом; r2 = хL1 = 16 Ом; хL2 = 20 Ом;хC2 = 32 Ом;r3 = хL3 = 100 Ом; хC1 = 12,5 Ом.
Определим комплексные сопротивления параллельных ветвей
Z1 = r1 + jхL1 = 12 + j16 Ом; Z2 = r2 + j(хL2 – хС2) = 16 – j12 Ом;
Z3 = r3= 100 Ом;Z4 = -jхС1 = -j12,5 Ом;Z5 = jхL3 = j100 Ом.
Комплексная проводимость всей цепи
Y =![]() +
+![]() +
+![]() +
+![]() =
=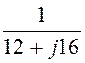 +
+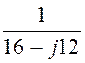 +
+![]() +
+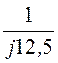 +
+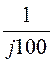 =
=
 = 0,08 + j0,06
= 0,1×e j36,9° См.
= 0,08 + j0,06
= 0,1×e j36,9° См.
Комплекс входного напряжения, соответствующий его синусоиде
U =![]() ×e –j30° В.
×e –j30° В.
По закону Ома определяем ток в неразветвлённой части цепи
I = Y×U = 0,1×e
j36,9°×![]() ×e
–j30° =
×e
–j30° =
= 21,21×e j6,9° А.
Следовательно, амперметр будет показывать 21,21 А.
ЗАДАЧА 3.32. В условиях задачи 3.25 определить показания приборов электродинамической системы, используя комплексный метод.
Направим по вещественной оси вектор входного напряжения, то есть примем U = U = 200 B.
Определим комплексные сопротивления ветвей
Z1 = r1 – jх1 = 6 – j8 Ом;Z2 = jх2 = j10 Ом; Z3 = r3 – jх3 = 5 – j15 Ом.
Комплексное сопротивление всей цепи
Z = Z1 +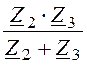 = 6
– j8 +
= 6
– j8 +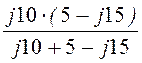 = 16 +j12 Ом.
= 16 +j12 Ом.
Ток источника I1 =![]() =
=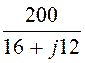 =
8 – j6 = 10×e –j36,9° А.
=
8 – j6 = 10×e –j36,9° А.
Токи параллельных ветвей
I2
= I1×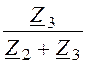 = 10×e –j36,9°×
= 10×e –j36,9°×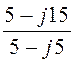 = 10 – j20 = 22,36×e –j63,4°А;
= 10 – j20 = 22,36×e –j63,4°А;
I3
= I1×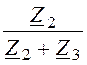 = 10×e –j36,9°×
= 10×e –j36,9°×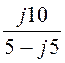 = -2 + j14 = 14,14×e j98,1°А.
= -2 + j14 = 14,14×e j98,1°А.
Напряжение на параллельных ветвях (измеряется вольтметром и подаётся на ваттметр)
UW = I2×Z2= 22,36×e –j63,4°·j10 = 223,6×e j26,6°= 200 + j100 B.
Показание ваттметра
PW = Re[UW ×![]() ] = Re[223,6×e j26,6°×10×e
j36,9°]= 1000
Bт.
] = Re[223,6×e j26,6°×10×e
j36,9°]= 1000
Bт.
Следовательно, показания приборов:
А1 ® 10 А; А2 ® 22,36 А; А3 ® 14,14 А;V® 223,6 B;W® 1000 Bт.
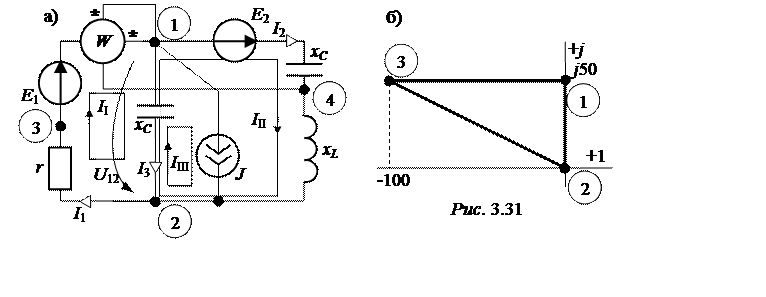
ЗАДАЧА 3.33. В схеме рис. 3.31,a известно: Е1 = Е2 = 100 В, причём Е2 опережает Е1 на 90° по фазе; J = 5 A, причём ток этого источника находится в противофазе с Е2; r = хC = 10 Ом; хL = 20 Ом.
Требуется определить токи во всех ветвях, показание ваттметра, составить баланс реактивных мощностей, построить топографическую диаграмму для контура 1-2-3-1.
 |
Совместим с вещественной осью вектор Е1, тогда для источников комплексы будут следующими:
Е1 = 100 В; Е2 = 100×e j90° = j100B;J = 5×e -j90° = -j5A.
Поскольку в схеме два узла, то расчёт токов
рационально произвести методом узлового напряжения U12
=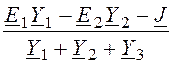 , где комплексные проводимости ветвей: Y1 =
, где комплексные проводимости ветвей: Y1 =![]() =
=![]() = 0,1 См;
= 0,1 См;
Y2 =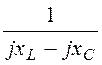 =
=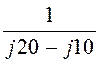 =
=![]() = -j0,1 См;
= -j0,1 См;
Y3 =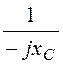 =
=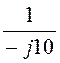 = j0,1
См.
= j0,1
См.
Тогда U12 =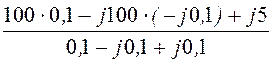 = j50
В.
= j50
В.
По закону Ома определяем токи:
I 1
=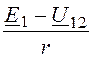 =
=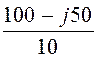 = 10 – j5 А;
= 10 – j5 А;
I 2 = (Е2 + U12)×Y2 = (j100 + j50)×(-j0,1) = 15 А;
I 3 = U12×Y3 = j50×j0,1 = -5 А.
Правильность определения токов проверим по первому закону Кирхгофа для узла 1: -I 1 + I 2 + I 3 + J= 0 или -10 + j5 +15 – 5 – j5 = 0.
Показание ваттметра: PW= Re[U14×(-![]() )].
)].
Тогда PW = Re[-j250×(-10– j5)] = -1250 Вт.
Баланс реактивных мощностей:
Qи =
Im[Е1×![]() + Е2×
+ Е2×![]() + (-U12)×
+ (-U12)×![]() ]=
Im[100×(10+j5)+j100×15 – j15×j5]=
2000 вар;
]=
Im[100×(10+j5)+j100×15 – j15×j5]=
2000 вар;
реактивная мощность приёмников
Qпр = I22×(хL – хС) + I32×(-хС) = 152×10 – 52×10 = 2000 вар.
Следовательно, баланс реактивных мощностей соблюдается.
При построении топографической диаграммы примем, что j 2= 0, тогда j 1= I3×(-jхС)= U12 = j50 В; j 3= j 1- Е1= -100 + j50 В; j 2 = j 3 + I1×r= 0.
На рис. 3.31,б приведена требуемая диаграмма.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.