![]() +
+ ![]() ×r23+
×r23+ ![]() ×x23+
×x23+ ![]() +
+
![]() ×r56+
×r56+ ![]() ×x56+
×x56+ ![]() =
=![]() =
=
![]() .
.
При этом ![]() =
=![]() ×x1 =10×8 = 80 Bи этот вектор напряжения опережает ток
×x1 =10×8 = 80 Bи этот вектор напряжения опережает ток ![]() на 90°;
на 90°;
I1×r23= 10×12 = 120 B, I1×x23= 10×16 = 160 B,
Ucd = I1×x4= 10×2 = 20 B, I1×r56= 10×8 = 80 B,
I1×x56= 10×4 = 40 B, I1×r1= Uef = 10×4 = 40 B.
На рис. 3.21 падения векторных напряжений ![]() ×r23,
×r23, ![]() ×x23,
×x23, ![]() ×r56,
×r56, ![]() ×x56 построены пунктирно, так как эти напряжения
отсутствуют в исходной схеме.
×x56 построены пунктирно, так как эти напряжения
отсутствуют в исходной схеме.
Далее переходим к построению векторов токов I2 и I3. Ток I3 перпендикулярен
напряжению Ubc, а ток ![]() =
=![]() -
-![]() .
.
Параллельно вектору Ude
откладывается ток I6, а ток ![]() =
=![]() -
-![]() стро-ится в
соответствии с первым законом Кирхгофа.
стро-ится в
соответствии с первым законом Кирхгофа.
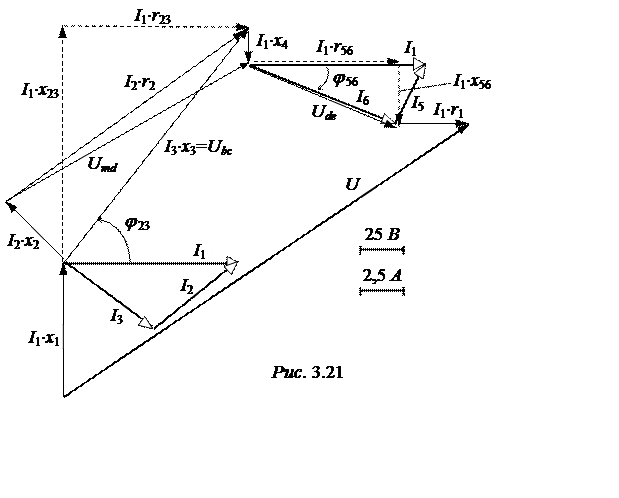 |
Векторная диаграмма принимает окончательный вид рис.
3.21. На этой векторной диаграмме указан также вектор напряжения ![]() .
.
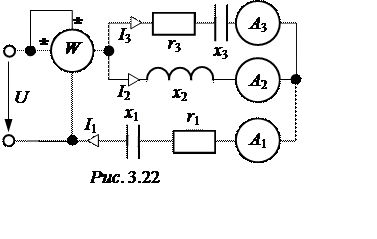 ЗАДАЧА 3.22.
В схеме рис. 3.22 известно:
ЗАДАЧА 3.22.
В схеме рис. 3.22 известно:
U = 200 B; r1 = 30 Ом; x1 = 50 Ом;
x2 = 10 Ом; r3 = 5 Ом; x3 = 15 Ом.
Определить показания приборов.
Решение
1. Заменяем параллельное соеди-нение ветвей 2 и 3 эквивалентным последовательным соединением сопротивлений r23 и x23:
g2 = 0; b2 =![]() =
=![]() = 0,1
Cм; Z3 =
= 0,1
Cм; Z3 =![]() =
=![]() =
=![]() = 5
= 5![]() Oм;
Oм;
g3 = ![]() =
=![]() =
0,02 Cм;
b3 =
=
0,02 Cм;
b3 =![]() =
=![]() =
0,06 Cм;
=
0,06 Cм;
g23 = g2 + g3 = 0 + 0,02 = 0,02 Cм; b23 = b2 – b3 = 0,1 – 0,06 = 0,04 Cм;
Y23 =![]() =
=![]() = 0,02
= 0,02![]() Cм; Z23
=
Cм; Z23
=![]() =
=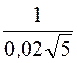 = 10
= 10![]() Oм;
Oм;
r23 =![]() =
=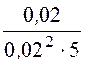 = 10 Ом;
x23 =
= 10 Ом;
x23 =![]() =
=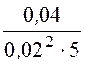 = 20 Ом.
= 20 Ом.
2. Входное сопротивление цепи и её коэффициент мощности:
Z
=![]() =
=![]() = 50 Oм;
= 50 Oм;
cosj =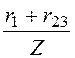 =
=![]() = 0,8.
= 0,8.
Действующее значение тока в неразветвлённой части цепи
(показание первого амперметра): I1 =![]() =
=![]() =
4 A.
=
4 A.
Напряжение на зажимах параллельных ветвей:
U23 = Z23×I1= 10![]() ×4 = 40
×4 = 40![]() B.
B.
Показания второго и третьего амперметров:
I2 =![]() =
=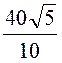 = 4
= 4![]() A;I3 =
A;I3 =![]() =
=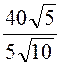 =
4
=
4![]() A.
A.
3. Ваттметр включен на измерение активной мощности цепи. Его показание:
P = U×I1×cosj = 200×4×0,8 = 640 Вт.
Активная мощность резисторов
PR = r1×I12
+ r2×I22
= 30×42 +
5×![]() = 640 Вт
= 640 Вт
равна активной мощности источника, то есть налицо выполнение баланса активных мощностей.
ЗАДАЧА 3.23. В схеме рис. 3.23,а известно:u(t) =100![]() ×sin(wt+30°)
B;
×sin(wt+30°)
B;
r1 = 5 Ом;xC1 = 8 Ом; r2 = 3 Ом; xC2 = 10 Ом; xL = 4 Ом.
Определить токи, коэффициент мощности, построить полную векторную диаграмму цепи. Задачу решить методом пропорциональных величин. Дополнительно ответить на вопросы: при каком xC2 будет резонанс токов? При каком xC1 будет резонанс напряжений?
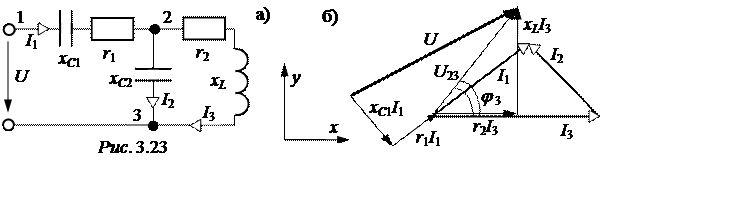 |
1. Построим качественно векторную диаграмму (ВД) (рис. 3.23,б). Построение следует начинать с самого дальнего от источника участка цепи (это – третья ветвь). Поскольку здесь имеется последовательное соединение сопротивлений, сначала строим вектор тока I3. Далее построение диаграммы ведётся от конца схемы к началу (источнику) с соблюдением законов Кирхгофа и правил построения ВД.
2. Расчёт выполняем в том же порядке, в каком строилась ВД.
Пусть
I3 = 1 A, т.е. i3(t) =![]() ×sin(wt) A. Тогда
×sin(wt) A. Тогда
Ur2 = r2×I3 = 3 B,
UxL =
xL×I3 = 4 B,
I2 =![]() =
=![]() = 0,5
A.
= 0,5
A.
Проекции векторов токов на оси х и у:
I3x = I3 = 1 A, I3y
= 0; j 3 = arctg![]() = arctg
= arctg![]() = 53,1°,
= 53,1°,
I2x = I2×cos(j 3 + 90°)= 0,5×(-0,8) = -0,4 A, I2y = I2×sin(j 3 + 90°)= 0,5×0,6 = 0,3 A.
Определяем первый ток по проекциям:
I1x = I2x + I3x = -0,4 + 1 = 0,6 A, I1y = I2y + I3y = 0,3 A,
I1 =![]() =
=![]() =
0,671 A.
=
0,671 A.
Определяем расчётное значение входного напряжения по проекциям:
UxC1 = xC1×I1 = 8×0,671 = 5,36 B; Ur1 = r1×I1 = 5×0,671 = 3,35 B,
Ux = UxC1×cos( 90° – yi1) + Ur1×cos(yi1) + Ur2 =
= 5,36×cos(90° – 26,6°) + 3,35×cos(26,6°) + 3 = 8,40 B,
Uy = UxC1×sin(yi1 – 90°) + Ur1×sin(yi1) + UxL =
= 5,36×sin(26,6° – 90°) + 3,35×sin(26,6°) + 4 = 0,707 B,
Uрасч
=![]() =
=![]() = 8,43 B,
= 8,43 B,
yUрасч
= arctg![]() = arctg
= arctg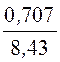 =
4,8°.
=
4,8°.
3. Коэффициенты пересчёта:
k
=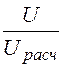 =
=![]() =
11,86; Dy =yU– yUрасч
= 30° – 4,8° = 25,2°.
=
11,86; Dy =yU– yUрасч
= 30° – 4,8° = 25,2°.
4. Получаем ответы i1(t) =
7,96![]() ×sin(wt + 51,8°) A;
×sin(wt + 51,8°) A;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.