i2(t) =
5,93![]() ×sin(wt + 168,4°) A;
×sin(wt + 168,4°) A;
i3(t) =
11,86![]() ×sin(wt + 25,2°) A.
×sin(wt + 25,2°) A.
5. Условие резонанса токов: b2 = b3.
b2 =![]() ; b3 =
; b3 =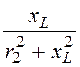 =
=![]() См; хС2 =
См; хС2 =![]() =
=![]() =
=![]() =
6,25 Ом.
=
6,25 Ом.
6. Условие резонанса напряжений хС1= х23, но Z23 =![]() =
=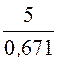 =
7,46 Ом,
=
7,46 Ом,
х23 = Z23×sin(j 3 – yi1) = 7,46×sin(53,1° – 26,6°) = 3,33 Ом.
Таким образом, резонанс напряжений наблюдается при хС1= 3,33 Ом.
3.3.2. Задачи для самостоятельного решения
 ЗАДАЧА 3.24.
Рассчитать мгновенные и действующие значения напряжений и токов схемы рис.
3.24, составить баланс активных и реактивных мощностей, построить полную
векторную диаграмму напряжений и токов, если:
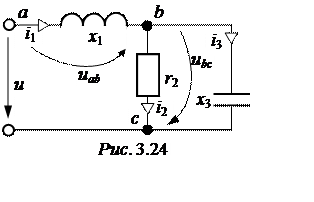
ЗАДАЧА 3.24.
Рассчитать мгновенные и действующие значения напряжений и токов схемы рис.
3.24, составить баланс активных и реактивных мощностей, построить полную
векторную диаграмму напряжений и токов, если:
u(t) = 200×sin(wt +120°) B;
х1 = 28 Ом; х3 = 24 Ом;r2 = 24 Ом.
Ответы: i1(t) = 10×sin(wt + 66,87°) A; uab(t) = 280×sin(wt +156,87°) B;
ubc(t) = 120![]() ×sin(wt +21,87°) B; i2(t)
= 5
×sin(wt +21,87°) B; i2(t)
= 5![]() ×sin(wt +21,87°) A;
×sin(wt +21,87°) A;
i3(t) = 5![]() ×sin(wt +111,87°) A; P = 600 Вт;
Q = 800 вар.
×sin(wt +111,87°) A; P = 600 Вт;
Q = 800 вар.
 ЗАДАЧА 3.25.
Методом проводимостей определить показания прибо-ров электродинамической
системы в схеме рис. 3.25, если: u= 200 B;
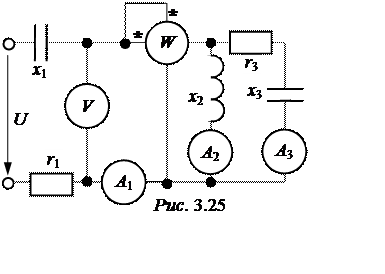
ЗАДАЧА 3.25.
Методом проводимостей определить показания прибо-ров электродинамической
системы в схеме рис. 3.25, если: u= 200 B;
х1 = 8 Ом; х2 = 10 Ом;r3 = 5 Ом;
х3 = 15 Ом;r1 = 6 Ом.
Построить векторную диаграм-му цепи.
Ответы: A1 ®10 A; V ® 224 B;
A2 ® 22,4 A; A3 ® 14,14 A;
W ® 1000 Вт.
3.3.3. Задачи повышенной сложности решения
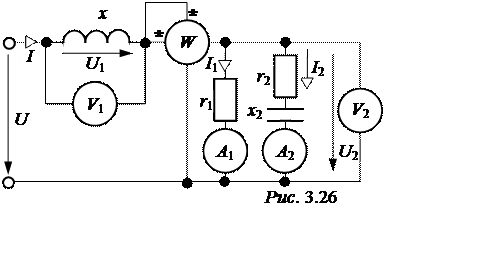 ЗАДАЧА 3.26.
Опре-делить напряжение и ток источника питания схемы рис. 3.26 и её параметры
по известным показаниям при-боров: V1® 80 B; V2®100 B;
ЗАДАЧА 3.26.
Опре-делить напряжение и ток источника питания схемы рис. 3.26 и её параметры
по известным показаниям при-боров: V1® 80 B; V2®100 B;
A1 ® 1 A;A2 ® 1,6 A;
W ® 180 Вт.
 Построить векторную диаграмму цепи.
Построить векторную диаграмму цепи.
Ответы:u= 81,47 B;i = 2,27 A;
r1 =100 Ом; х = 35,2 Ом; х2 = 54,13 Ом.
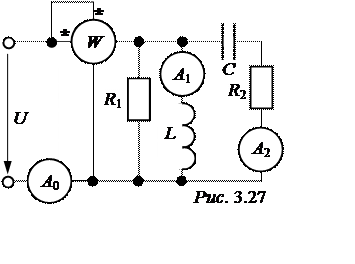
ЗАДАЧА 3.27. Цепь рис. 3.27 находится в состоянии резонанса. Ваттметр показывает 100 Вт, ампер-метры A1 и A2 – 4 и 5 А, R1 = R2. Требуется определить хL, хC и показа-ние амперметра А0.
Ответы:i0 = 11,33 A; хL = 2,205 Ом; хC = 1,41 Ом.
 3.3.4. Применение ПЭВМ для решения задач на метод
проводимостей
3.3.4. Применение ПЭВМ для решения задач на метод
проводимостей
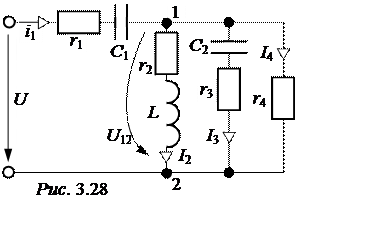
ЗАДАЧА 3.28. В схеме рис. 3.28 рассчитать все токи, составить баланс активных и реактивных мощностей, если u= 200 B;
r1 = r2 = 2 Ом; r3 = 4 Ом; r4 = 20 Ом;хC1 = хC2 = 8 Ом;хL = 6 Ом.
Программа решения задачи в системе MathCAD
Исходные данные
u:= 200 r1 := 2 r2 := 2 r3 := 4 r4 := 20 хC1 := 8 хC2 := 8 хL := 6
Определяем полные сопротивления, а также активные и реактивные проводимости параллельно включенных ветвей
Z2
:=![]() Z3 :=
Z3 :=![]() g2 :=
g2 :=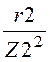 g3 :=
g3 :=![]() g4 :=
g4 :=![]()
b2
:=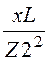 b3 :=
b3 :=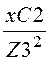 b4 := 0
b4 := 0
ge := g2 + g3 + g4 be := b2
– b3 + b4 ye := ![]()
Полное, активное и реактивное сопротивления эквивалентной ветви
Ze := ye -1 re := ge×Ze2 xe := be×Ze2
Ток в неразветвлённой части цепи I1
:=![]()
Напряжение на параллельно включенных ветвях U12 :=I1×Ze
Токи
в параллельно включенных ветвях I2 :=![]() I3 :=
I3 :=![]() I4 :=
I4 :=![]()
Ответы для токов в А I1 = 20 I2 = 20 I3 = 14.142 I4 = 6.325
Активная и реактивная мощности источника
Pi := U×I1×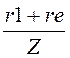 Qi := U×I1×
Qi := U×I1×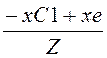 Pi = 3.2´103 Qi
= -2.4´103
Pi = 3.2´103 Qi
= -2.4´103
Pp := I12×r1+I22×r2+I32×r3+I42×r4 Qp := -I12×xC1+I22×xL-I32×xC2
Pp = 3.2´103 Qp = -2.4´103
Следовательно, балансы мощностей сходятся.
3.4. Комплексный (символический) метод
ЗАДАЧА 3.29. Решить задачу 3.2 комплексным методом.
Исходные данные представим комплексными числами:
комплексная амплитуда напряжения сетиUm = Um×e jyu = 200×e – j20°B;
комплексное сопротивление цепи r-L
Z = r + jwL = 35 + j2p×50×80×10-3 = 35 + j25,12 = 43,1×e j35,67° Ом.
По закону Ома рассчитаем комплексную амплитуду тока
Im =![]() =
=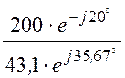 = 4,64×e –j55,67° А.
= 4,64×e –j55,67° А.
Мгновенное значение тока
i(t) = Im![]() = Im
= Im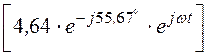 =
=
= Im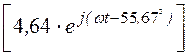 = 4,64×sin(wt–55,67°) A.
= 4,64×sin(wt–55,67°) A.
Комплексная мощность на входе цепи
S =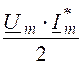 =
=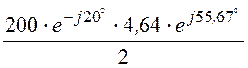 = 464×e j35,67° = 377 + j270,5 ВА = Р +
jQ.
= 464×e j35,67° = 377 + j270,5 ВА = Р +
jQ.

ЗАДАЧА 3.30. В схеме рис. 3.29 определить действую-щее и мгновенное значение напряжения на ёмкости, если
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.