Линейные цепи синусоидального тока. Основные теоретические положения, страница 11

I_I×(r – jх_С) – I_II×(-jх_С) – J×(-jх_С) = Е₁;

-I_I×(-jх_С) + I_II×(jх_L – 2jх_С) + J×(-jх_С) = Е₂.

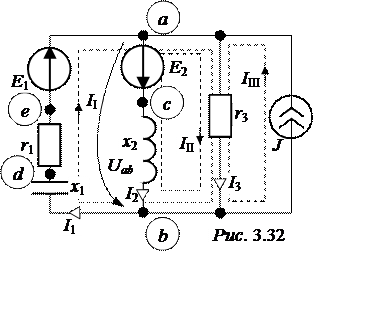ЗАДАЧА 3.34. В схеме рис.3.32 известно: Е₁ = 380 В, Е₂ = j100 В,

J = 10×е ^j45° A,     r₁ = 10 Ом,

х₁= 14,29 Ом, r₃ = 6 Ом,  х₂ = 3,3 Ом.

Рассчитать токи методом двух узлов, выполнить проверочный расчёт методом контурных токов, составить баланс мощностей, построить топографическую диаграмму цепи, совмещённую с векторной диаграммой токов.

Решение

1. Сопротивления ветвей в комплексной форме:

Z₁ = r₁ – jх₁ = 10 – j14,29 Ом; Z₂ = jх₂ = j3,3 Ом;Z₃ = r₃ = 6 Ом.

2. Расчёт токов методом двух узлов:

U_ab ==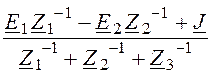

==

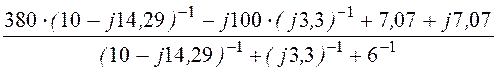= 83,60×е ^j165,4°= -80,89 + j21,09 В.

I₁ =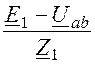==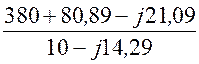 26,45×е ^j52,4°= 16,14 + j20,96 А;

I₂ =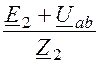==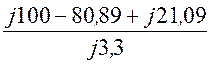 44,13×е ^j33,7°= 36,70 + j24,51 А;

I₃ ===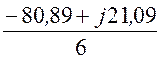 13,93×е ^j165,4°= -13,48 + j3,52 А.

3. Система уравнений для контурных токов:

(Z₁ + Z₃)×I_I + Z₃×I_II= Е₁ - Z₃×J;         (10–j14,29+6)×I_I + 6×I_II= 380 - 6×(7,07+j7,07);

Z₃×I_I + (Z₂ + Z₃)×I_II= -Е₂ - Z₃×J.        6×I_I + (j3,3 + 6)×I_II= -j100 - 6×(7,07 + j7,07).

Решение системы с помощью определителей:

D= 112,1×е ^–j17,1°;D_I= 2966×е ^j35,1°;D_II = 4947×е ^–j163,3°;

I_I ===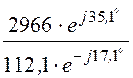 26,45×е ^j52,4° А; I_II ===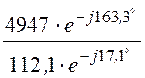 -44,13×е ^j33,8° А.

Токи ветвей, вычисленные через контурные токи:

I₁ = I_I = 26,45×е ^j52,4° А;

I₂ = -I_II = 44,13×е ^j33,7° А;

I₃ = I_I + I_II + J =16,14 + j20,96 – 36,70 – j24,51 + 7,07 + j7,07 = -13,49 + j3,52 А.

4. Комплексная мощность источников:

S_и = Е₁×+ Е₂×+ U_ab×=

= 380×(16,14 + j20,96) + j100×(36,70 + j24,51) + (-80,89 + j21,09)×(7,07 – j7,07)=

= 8162 – j3573 ва.

Активная и реактивная мощности приёмников:

P_пр = I₁²×r₁ + I₃²×r₃ = 26,45²×10 + 13,93²×6 = 8160вт;

Q_пр = I₁²×(-х₁) + I₂²×х₂ = -26,45²×14,29 + 44,13²×3,3 = -3571 вар.

Поскольку P_пр»Re(S_и) и Q_пр»Im(S_и), то баланс мощностей выполняется.

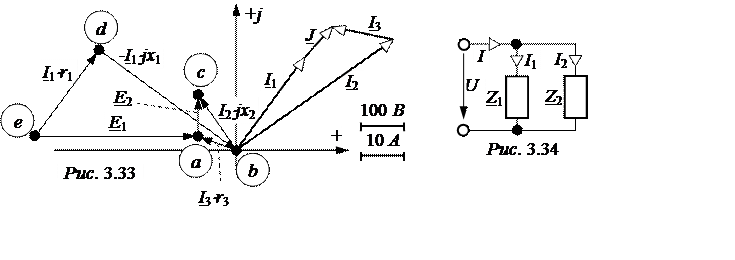5. Вычислим значения комплексов потенциалов разных точек цепи. Примем j _b= 0, тогда  j _a= U_ab = -80,89 + j21,09 В.

Остальные потенциалы j _c= j _a+ Е₂ = -80,82 + j121,09 В;

j _e= j _a– E₁ = -460,89 + j21,09 В;

j _d= -I₁×(-jх₁) = 378,0×е ^j142,4° В.

Диаграмма приведена на рис. 3.33.

3.4.2. Задачи для самостоятельного решения

ЗАДАЧА 3.35. Символическим методом решить задачу 3.3.

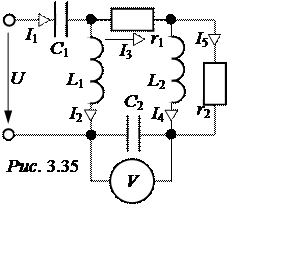
ЗАДАЧА 3.36. Определить токи во всех ветвях цепи рис. 3.34, если

U = 130 В;    Z₁ = 6 + j8 Ом;Z₂ = 5 – j12 Ом.

Ответы:I = 11,71×е ^-j5,73° А;    I₁ = 13×е ^-j53,1° А;    I₂ = 10×е ^j67,4° А.

ЗАДАЧА 3.37. Два электродвигателя с номинальными данными  P_1н= = 20 кВт;   U_1н= 220 В;   cosj_1н= 0,8 (j_1н>0);  P_2н= 30 кВт;   U_2н= 220 В; cosj_2н= 0,6 (j_2н <0); включены параллельно и питаются через линию электро-передачи, обладающей комплексным сопротивлением  Z_л = 3 + j4 Ом. Двига-тели нагружены номинальной нагрузкой. Требуется определить напряжение и полную мощность источника питания при условии, что напряжение на двигателях номинальное.

Ответы:U₁ = 217 В;  S₁ = 57,84 кВА. 

ЗАДАЧА 3.38. В схеме рис. 3.35 требует-ся определить все токи и входное напряжение, если вольтметр показывает 50 В, а параметры цепи: r₁= х_С2= 5 Ом;  х_С1 = r₂ = х_L1= х_L2 =10 Ом.

Ответ: если по вещественной оси направить вектор напряжения вольтметра, то

I₁ = 10 + j10 A;   I₂ = 10 A;   I₃ = j10 A;

I₄ = 5 + j5 A;    I₅ = -5 + j5 A;   U = 100 В. 

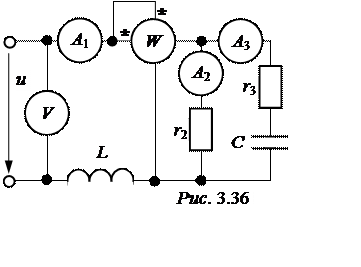
ЗАДАЧА 3.39. В схеме рис. 3.36 определить показания приборов, построить векторную диаграмму, проверить баланс мощностей. Задачу решить методами проводимостей и символическим. Известно:

u(t) = 6×sin(100t +) B,  L = 0,06 Гн,

r₃ = 6 Ом,r₂ = 10 Ом,C = 833 мкФ.

Ответы:Z₃ = 6×e ^–j63,4° Ом;Z₂₃ = 6 – j3 Ом;Z = 6 + j3 Ом;

I₁ = 2×e ^j18,4° A;   I₂ = 0,6×e ^–j8,2° A;   I₃ = 1×e ^j55,3°  A;   P_W = 24 Вт.

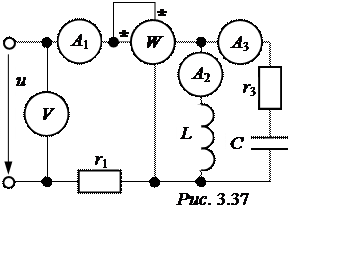
ЗАДАЧА 3.40. В схеме рис. 3.37 определить показания приборов, построить векторную диаграмму, проверить баланс мощностей. Задачу решить

 методами проводимостей и символиче-ским. Известно:

u(t) = 40×sin(100t+) B, L = 0,1 Гн,

r₁ = r₃ = 10 Ом,C = 1000 мкФ.

Ответы: Z₃ = 10×e ^–j45° Ом;