i3(t) = I3![]() ×sin(wt+yubd – j 3) = 10
×sin(wt+yubd – j 3) = 10![]() ×sin(wt + 45°) А;
×sin(wt + 45°) А;
где yubd = yu– j вх– j 23 = -90° + 45° + 45° = 0.
Проверим баланс активных мощностей: U×I1×cosj вх = I12×r1 + I32×r3.
![]() ×10×cos(-45°) = 102×10+102×20 или 3000 Вт = 3000 Вт.
×10×cos(-45°) = 102×10+102×20 или 3000 Вт = 3000 Вт.
Проверим баланс реактивных мощностей:
U×I1×sinj вх = I12×(-x4) + I22×x2 + I32×(-x3).
![]() ×10×sin(-45°)=102×(-50)+(10
×10×sin(-45°)=102×(-50)+(10![]() )2×20+102×(-20) или -3000 вар = -3000 вар.
)2×20+102×(-20) или -3000 вар = -3000 вар.
 Вывод: балансы активных и реактивных мощностей
сходятся, следовательно, задача решена верно и можно переходить к построению
полной векторной диаграммы.
Вывод: балансы активных и реактивных мощностей
сходятся, следовательно, задача решена верно и можно переходить к построению
полной векторной диаграммы.
Рассчитаем неизвестные напряжения на элементах электрической цепи.
Uab = I1×r1= 10×10 = 100 В; Ubc = I3×r3= 10×20 = 200 В;
Uca = I3×x3= 10×20 = 200 В; Ude = I1×x4= 10×50 = 500 В.
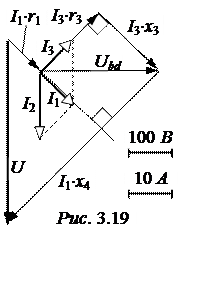
Векторная диаграмма приведена на рис. 3.19. Её построение начинается с выбора масштабов напряжений и токов. Затем в произвольном направлении строится вектор напряжения на параллельно включенных ветвях Ubd, от которого под углами j 2, j 3, j 23 строятся векторы токов I2, I3 и I1, соответственно. При этом следует учесть, что I1 = I2 + I3.
 Остальные векторы напряжений строятся в соответствии с
уравнениями второго закона Кирхгофа и порядком расположения элементов
эквивалентной схемы (см. рис. 3.18,б):
Остальные векторы напряжений строятся в соответствии с
уравнениями второго закона Кирхгофа и порядком расположения элементов
эквивалентной схемы (см. рис. 3.18,б):
Uab + Ubd + Ude = U.
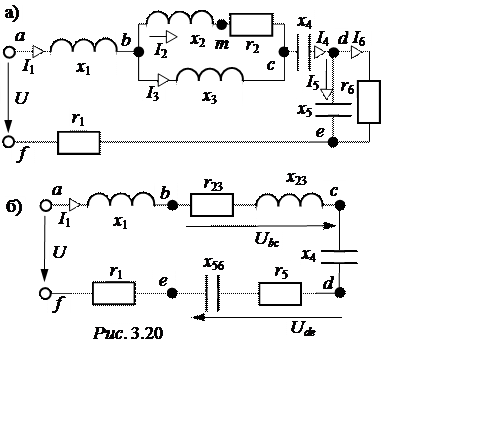
ЗАДАЧА 3.21. Рас-считать действующие значе-ния напряжений и токов в схеме рис. 3.20,а, проверить балансы активных и реак-тивных мощностей, постро-ить полную векторную диаг-рамму напряжений и токов, если: U = 300 B;r2 = 30 Ом, x2 = 10 Ом; x3 = 33,33 Ом; x4 = 2 Ом;
x5 = 20 Ом; r6 = 10 Ом; x1 = 8 Ом; r1 = 4 Ом.
Решение
В рассматриваемой схеме два разветвления: на участке bc параллельно включены 2я и 3я ветви, которые могут быть заменены эквивалентной ветвью r23-x23 (рис. 3.20,б); на участке de параллельно включены 5я и 6я ветви, заменяемые последовательной эквивалентной цепью r56-x56. Замена осуществляется на основании соотношений между активными и реактивными проводимостями параллельных ветвей:
g2 =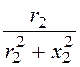 =
=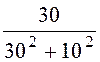 =
0,03 Cм; b2 =
=
0,03 Cм; b2 =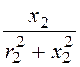 =
=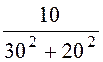 =
0,01 Cм (инд.);
=
0,01 Cм (инд.);
g3 =
0; b3 =![]() =
=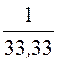 =
0,03 Cм (инд.);
=
0,03 Cм (инд.);
g23 = g2 + g3 = 0,03 + 0 = 0,03 Cм; b23 = b2 + b3 = 0,01 + 0,03 = 0,04 Cм (инд.);
r23
=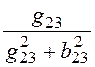 =
=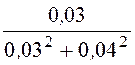 = 12 Ом;
= 12 Ом;
x23 =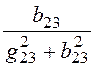 =
=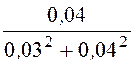 = 16 Ом
(инд.).
= 16 Ом
(инд.).
g5 = 0; g6 =![]() =
=![]() = 0,1
Cм; b5 =
= 0,1
Cм; b5 =![]() =
=![]() =
0,05 Cм (ёмк.);
b6 = 0;
=
0,05 Cм (ёмк.);
b6 = 0;
g56 = g5 + g6 = 0 + 0,1 = 0,1 Cм; b56 = b5 + b6 = 0,05 + 0 = 0,05 Cм (ёмк.);
r56 =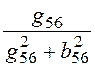 =
=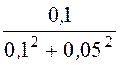 = 8 Ом;x56 =
= 8 Ом;x56 =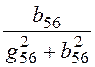 =
=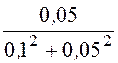 = 4 Ом
(ёмк.).
= 4 Ом
(ёмк.).
Входное сопротивление цепи по эквивалентной схеме (рис. 3.20,б)
Zвх =![]()
=![]() = 30 Ом;
= 30 Ом;
cosj вх
=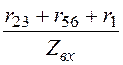 =
=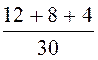 = 0,8;
= 0,8;
sinj вх
=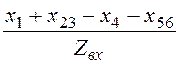 =
=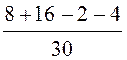 = 0,6.
= 0,6.
Ток в общей части схемы I1 = I4 =![]() =
=![]() = 10 A, напряжения
на разветвлениях Ubc =
I1×
= 10 A, напряжения
на разветвлениях Ubc =
I1×![]() = 10
= 10![]() = 200 B,
= 200 B,
Ude =
I1×![]() = 10
= 10![]() = 40
= 40![]() B, токи
в остальных ветвях
B, токи
в остальных ветвях
I2 =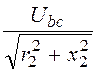 =
=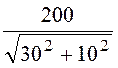 =
2
=
2![]() A, I5 =
A, I5 =![]() =
=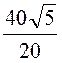 = 2
= 2![]() A,
A,
I3 =![]() =
=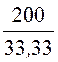 =
6 A,
I6 =
=
6 A,
I6 =![]() =
=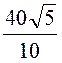 = 4
= 4![]() A.
A.
Проверим балансы мощностей. Баланс активных мощностей представляется для схемы рис. 3.20,а выражением
U×I1×cosj вх = I12×r1 + I22×r2 + I62×r6,
300×10×0,8 = 102×4+![]() ×30+
×30+![]() ×30 или 3000 Вт = 3000 Вт -
выполняется.
×30 или 3000 Вт = 3000 Вт -
выполняется.
Баланс реактивных мощностей цепи
U×I1×sinj вх = I12×x1 + I22×x2 + I32x3 – I42×x4 – I52×x5,
300×10×0,6 = 102×8 +![]() ×10 + 62×33,33 – 102×2 –
×10 + 62×33,33 – 102×2 – ![]() ×20 или 1800 вар = 800 + 400 + 1200 – 200 – 400 вар
- выполняется.
×20 или 1800 вар = 800 + 400 + 1200 – 200 – 400 вар
- выполняется.
Так как оба баланса мощностей выполняются, задача расчёта цепи решена верно, и можно переходить к построению векторной диаграммы.
Так как в схеме рис. 3.20,а имеется два разветвления, то сначала строится векторная диаграмма для последовательной эквивалентной схемы рис. 3.20,б и построение начинается с выбора произвольного направления вектора тока I1 последовательной цепи (горизонтально, вправо) (рис. 3.21).
Уравнение по второму закону Кирхгофа запишем в векторной форме с соблюдением принципа: падения напряжений на элементах схемы строго следуют в соответствии с расположением элементов, и каждому вектору напряжения присваиваются соответствующие индексы точек схемы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.