системой линейных дифференциальных уравнений по законам Кирхгофа i1(t) = i2(t) + i3(t),
r1i1 + r2i2
+ L
= E,
r1i1 + (r3 + r4)·i3 = E, решение которой будем искать в виде iq(t) = iqпр(t)+iqсв(t); uL(t) = uLпр(t)+uLсв(t).
3. Принуждённый режим:
i1пр
=
=
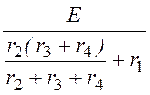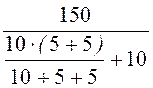= 10 А;
i2пр
= i1пр·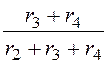
= 10·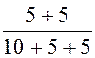
= 5 А;
i3пр = i1пр – i2пр = 10 – 5 = 5 А, uLпр = 0.
4. Свободный режим.
Составим
характеристическое уравнение путём записи входного сопротивления в операторной
форме (2-й способ):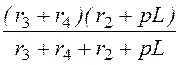 
+
r1 = 0.
Но можно составить характеристическое уравнение и относительно ветви с накопителем, при этом источник заменяется его внутренним сопротивлением (рис. 7.21). Тогда вид уравнения будет проще:
+ r2 + pL = 0;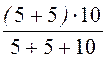 
+
10 + 20·10 -3·p =
0; p =
-750 c -1.
Тогда i1св = А1еpt = А1е -750t; i2св = А2е -750t; i3св = А3е -750t; uLсв =Bе -750t.
Постоянные интегрирования определим при t = 0+.
I способ решения
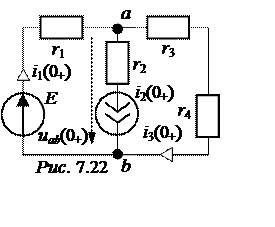
Схема после коммутации для t = 0+ имеет вид рис. 7.22. По методу двух узлов
uab(0+) =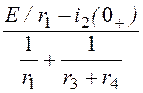
=
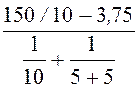= 56,25 B.
Токи в момент коммутации
i1(0+) =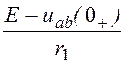
=
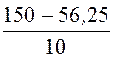= 9,375 А,
i3(0+)
=
=
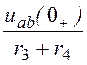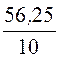= 5,625 А или i3(0+)
= i1(0+) – i2(0+) =
5,625 А,
uL(0+) = uab(0+) – r2i2(0+) = 56,25 – 10·3,75 = 18,75 B.
Запишем свободные составляющие при t = 0+:
i1св(0+) = А1 = i1(0+) – i1пр = 9,375 – 10 = -0,625 А,
i2св(0+) = А2 = i2(0+) – i2пр = 3,75 – 5 = -1,25 А,
i3св(0+) = А3 = i3(0+) – i3пр = 5,625 – 5 = 0,625 А,
uLсв(0+) = B = uL(0+) – uLпр = 18,75 – 0 = 18,75 B.
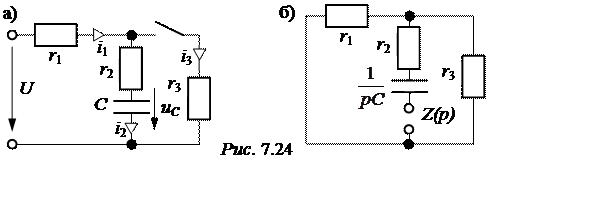
Итак: i1св(t) = -0,625е -750t А, i1(t) = 10 – 0,625е -750t А,
i2св(t) = -1,25е -750t А, i2(t) = 5 – 1,25е -750t А,
i3св(t) = 0,625е -750t А, i3(t) = 5 + 0,625е -750t А,
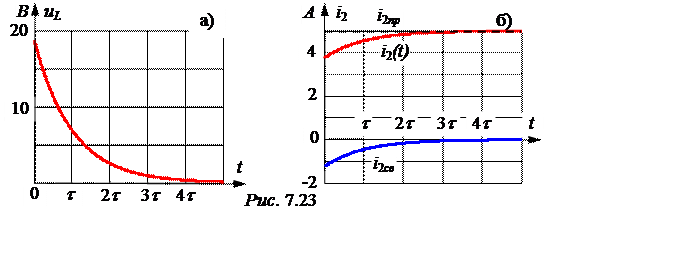
uL(t) = uLсв(t) = 18,75е -750t B.
II способ решения
Постоянную интегрирования А2 можно определить сразу, так как ток
i2 подчиняется первому закону коммутации:
А2 = i2(0+) – i2пр = 3,75 – 5 = -1,25 А,
i2св(t) = А2е -750t = -1,25е -750t А, i2(t) = i2пр(t) + i2св(t) = 5 – 1,25е -750t А.
Определим напряжение на индуктивности
uL(t) = L= 20·10 -3·(-1,25)(-750)е
-750t = 18,75е -750t B.
Узловое напряжение
uab(t) = r2i2(t) + uL(t) = 10·(5 – 1,25е -750t) + 18,75е -750t = 50 + 6,25е -750t B.
Токи i3(t)
=
=
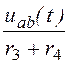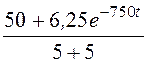= 5 + 0,625е -750t А,
i1(t) = i2(t) + i3(t) = 5 – 1,25е -750t + 5 + 0,625е -750t = 10 – 0,625е -750t А.
5. Построим графики i2(t) и uL(t). Длительность переходного процесса
ТПП = 4t=
=
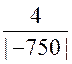с = 5,33 мс.
Результаты расчётов представим в виде табл. 7.2.
Таблица 7.2
|
t, мс |
0 |
1,33 |
2,67 |
4 |
5,33 |
|
i2св,А |
-1,25 |
-0,46 |
-0,17 |
-0,06 |
-0,02 |
|
i2,А |
3,75 |
4,54 |
4,83 |
4,94 |
4,98 |
|
uL, В |
18,75 |
6,9 |
2,54 |
0,93 |
0,34 |
 |
 |
Решение
1. Состояние цепи до коммутации: i1(t-) = i2(t-) = 0, uC(t-) = U= 50 В. В соответствии со вторым законом коммутации независимое начальное условие – uC(0+) = uC(0-) = 50 В.
2. Согласно классическому методу искомые переходные токи записываются в виде суммы принуждённых и свободных составляющих:
i1 = i1пр + i1св, i2 = i2пр + i2св, i3 = i3пр + i3св.
3. Рассчитываем принуждённые составляющие токов:
i2пр
= 0; i1пр = i3пр =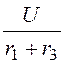
=
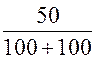= 0,25 А.
3. Характеристическое
уравнение составим, используя входное сопротивление в операторной форме (см. 7.1.1,
второй способ составления характеристического уравнения): Z(p) =
+ r2
+
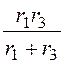= 0.
Корень характеристического уравнения:
p = -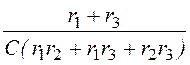
= -
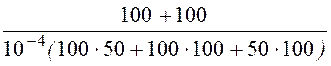= -100
с –1.
4. Свободные составляющие токов при одном корне характеристиче-ского уравнения: i1св = А×е рt, i2св = В×е рt, i3св = D×е рt.
5. Постоянные интегрирования А, В, D находятся с использованием начальных условий, которые, однако, можно получить разными способами. Рассмотрим некоторые из них.
а)
первый способ. Составляется система уравнений по законам Кирхгофа для
послекоммутационного режима для начального момента времени: i1(0) – i2(0)
– i3(0) = 0,
i1(0)×r1 + i2(0)×r2 + uC(0) = U,
i1(0)×r1 + i3(0)×r3 = U.
С числовыми значениями:
i1(0) – i2(0) – i3(0)
= 0,
i1(0)×100 + i2(0)×50 + 50 = 50,
i1(0)×100 + i3(0)×100 = 50.
Решение системы: i1(0) = 0,125 А, i2(0) = -0,25 А, i3(0) = 0,375 А.
Постоянные интегрирования:
А = i1св(0) = i1(0) – i1пр = 0,125 – 0,25 = -0,125;
В = i2св(0) = i2(0) – i2пр = -0,25 – 0 = -0,25;
D = i3св(0) = i3(0) – i3пр = 0,375 – 0,25 = 0,125.
б) второй
способ. Расчёт выполняется по эквивалентной схеме, составленной на
начальный момент времени. Здесь используется следствие из законов коммутации:
индуктивность в момент коммутации ведёт себя как источник тока с током iL(0),
ёмкость – как источник ЭДС с напряжением uC(0).
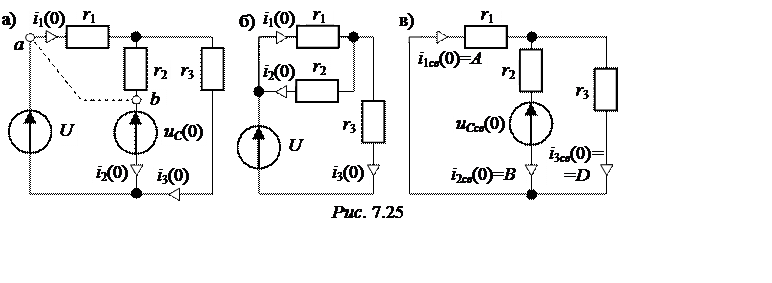
Для начального момента времени, таким образом, получаем схему рис. 7.25,а.
Учитывая, что в цепи оказались два одинаковых источника uC(0)
= U, можем утверждать, что потенциалы точек а
и b одинаковы, и точки можно соединить
перемычкой. Получаем схему рис. 7.25,б, из которой находим начальные значения
токов: i3(0)
=
=
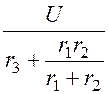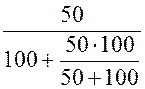= 0,375 А,
i1(0) = i3(0)×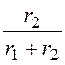
= 0,375×
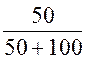= 0,125 А,
i2(0) = i1(0) –i3(0) = 0,125 – 0,375 = -0,25 А.
Далее постоянные интегрирования определяются как в первом способе.
 |
uCсв(0) = uC(0) – uCпр = 50 – 25 = 25 В.
Постоянные интегрирования: В =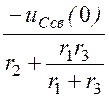
=
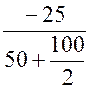= -0,25;
А = В×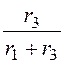
= -0,25×
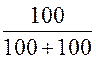= -0,125,
D= -В×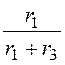
= 0,25×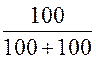= 0,125.
6. Записываем окончательные выражения для токов:
 |
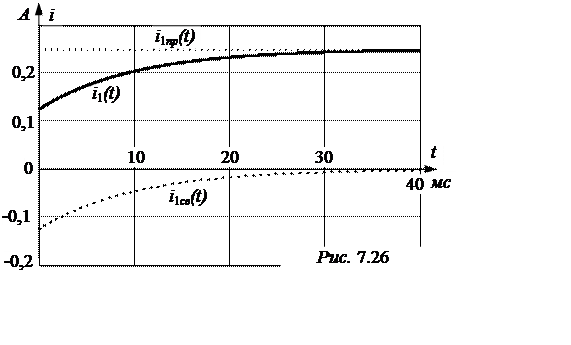7. Для построения графика i1(t) вычислим:
- постоянная времени цепи t = 1/|p| = 1/100 c = 10 мс,
- практическая длительность переходного процесса Тпп = (3¸5)t = 4×t = 40 мс.
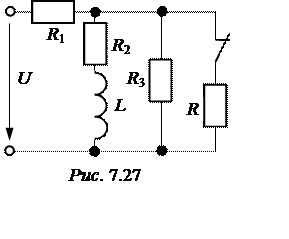График представлен на рис. 7.26.
ЗАДАЧА 7.11. В схеме рис. 7.27 рассчитать токи переходного процесса. Параметры цепи: U= 60 В, r1 = 9 Ом,
r2 = r3 = 30 Ом, r = 10 Ом, L= 0,4 Гн.
Ответы: i1(t) = 2,5 – 0,346×е –92,3t A;
i2(t) = 1,25 – 0,450×е –92,3t A;
i3(t) = 1,25 + 0,104×е –92,3t A.
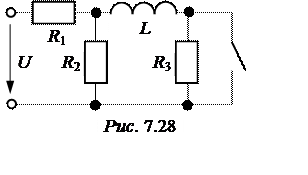ЗАДАЧА 7.12.
В схеме рис. 7.28 рассчитать токи переходного процесса. Параметры цепи:
U= 300 В, r1 = r2 = r3 = 100 Ом, L= 0,5 Гн.
Ответы: i1(t) = 3 – е –100t A;
i2(t) = е –100t A;
i3(t) = 3 – 2×е –100t A.
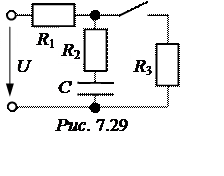
ЗАДАЧА 7.13. В схеме рис. 7.29 рассчитать напряжение на конденсаторе и токи переходного процесса. Параметры цепи: U= 100 В, r1 = 50 Ом, r2 = r3 = 100 Ом, С = 60 мкФ.
Ответы: uС(t) = 66,67 + 33,33×е –125t В;
i1(t) = 0,667 – 0,167×е –125t A; i2(t) = -0,250×е –125t A; i3(t) = 0,667 + 0,083×е –125t A.
ЗАДАЧА 7.14. Решить задачу 7.13 со следующими числовыми данными:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
