Операторный метод расчёта ПП. Основные теоретические положения

7.2. ОПЕРАТОРНЫЙ МЕТОД РАСЧЁТА ПП

7.2.1. Основные теоретические положения

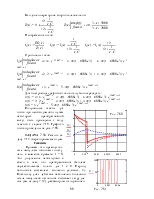
Сущность операторного метода заключается в том, что от некоторой функции вещественного переменного (например, времени t), называемой оригиналом f(t), переходят к функции комплексного переменного f(р), называемой изображением. При этом дифуравнения относительно оригиналов превращаются в алгебраические уравнения относительно изображений, решение которых проще.

Изображение и оригинал функции связывают формулой прямого преобразования Лапласа    f(р) =.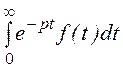

В справочной литературе имеются таблицы оригиналов и соответствующих им изображений. Изображения наиболее характерных оригиналов приведены в табл. 7.3.

Таблица 7.3

Закон Ома для последовательного участка R-L-C:

I(р) =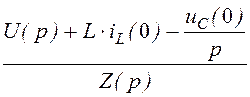, где  Z(р) = R + pL +  – операторное сопротивление этого участка.

В числителе кроме изображения напряжения на зажимах участка U(р) фигурируют внутренние операторные ЭДС  Li_L(0)  и 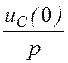 , учитывающие независимые начальные условия.

Iзакон Кирхгофа:  для любого узла   S±I(р) = 0.

IIзакон Кирхгофа:  для любого контура

=.

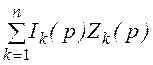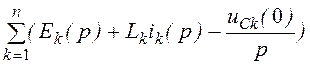Поскольку законы Ома и Кирхгофа в операторной форме имеют такой же вид, как и в цепях постоянного тока (ЦПТ), то все методы анализа ЦПТ, основанные на этих законах, могут быть применены для анализа операторных схем с учётом независимых начальных условий.

По изображениям искомых величин, полученным в результате анализа операторной схемы, находят оригиналы искомых величин. Для этого применяют обратное преобразование Лапласа или используют таблицу преобразований Лапласа, или пользуются теоремой разложения.  В последнем случае изображение искомой величины приводят к виду:

f(р) =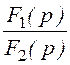  или 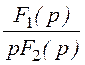  , гдеf₁(р) и  f₂(р) – степенные многочлены:

f₁(р) = b_m p^m + b_m-1 p^m-1 + … + b₁ p + b₀,     f₂(р) = a_n pⁿ + a_n-1 p^n-1 + … + a₁ p + a₀, причём  m £ n  и дробь несократима (числитель и знаменатель не имеют одинаковых корней). Оригинал определяется по формулам:

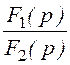® f(t) = 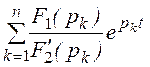 или 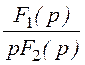 ® f(t) =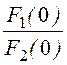+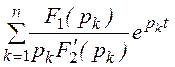, где  p_k– корни уравнения    f₂(р) = 0,  а  n – число корней этого уравнения,

f₁(р_k) и f₂¢(р_k) – значения многочлена f₁(р) и производной от многочлена f₂(р) при k-м корне.

В случае пары комплексных сопряжённых корней можно использовать следующие формулы: 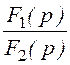    ®    f(t) = 2Re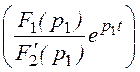

или 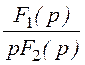   ®   f(t) =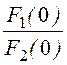+ 2Re.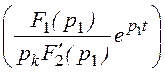

Рекомендуемая последовательность расчёта ПП операторным методом.

1. Расчётом цепи до коммутации определяют независимые начальные условия  i_L(0), u_C(0)  и записывают величины внутренних операторных ЭДС Li_L(0) и  .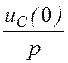

2. Для цепи после коммутации составляется эквивалентная операторная схема.

3. Любым методом анализа ЦПТ определяют изображения требуемых токов и напряжений, приводя затем их к виду рациональной дроби.

4. По теореме разложения или с помощью обратных преобразований Лапласа находят оригиналы искомых токов и напряжений переходного процесса.

7.2.2. ПП в цепях с одним накопителем

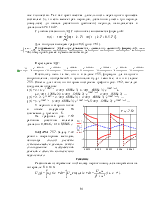
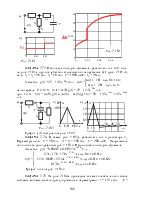
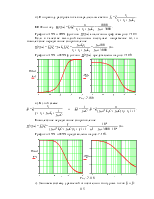
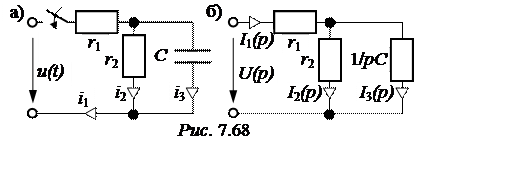
ЗАДАЧА 7.45. Напряжение, приложен-ное к цепи рис. 7.68,а изменяется по закону

u(t) = 30t² + 18t + 10 В.

Параметры цепи:  r₁ = r₂ =

= 100 Ом,  С = 10 мкФ.

Рассчитать ток конденсатора.

Решение

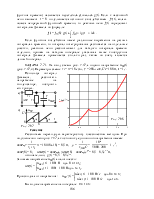
До появления напряжения на источнике цепь находилась в состоянии покоя. Поэтому данная задача – с нулевыми начальными условиями, а эквивалентная операторная схема выглядит так, как на рис. 7.68,б.

Изображение приложенного напряжения определяем, используя таблицу преобразований Лапласа:  U(p) =++.

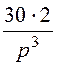Изображения первого и третьего токов:   I₁(p) =;  

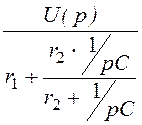I₃(p) ==×==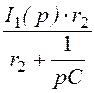

=++.

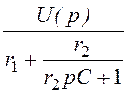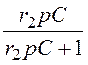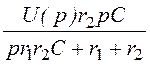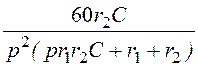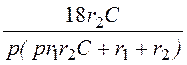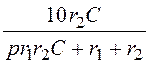Разложим последнее выражение на простые дроби:

I₃(p) =++.

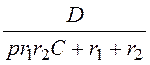Приведя в выражениях для I₃(p) дроби к общему знаменателю и приравняв числители, получим следующее уравнение:

Ар(рr₁r₂C + r₁ + r₂) + B(рr₁r₂C + r₁ + r₂) + Dp² = 60r₂C + р×18r₂C + р²×10r₂C.

Приравниваем коэффициенты при одинаковых степенях р и получаем систему уравнений:

коэффициенты при   p² :     АСr₁r₂ + D = 10r₂C;

при   p :     А(r₁ + r₂) + ВСr₁r₂ = 18r₂C;

при   1 :     В(r₁ + r₂) = 60r₂C.

Отсюда   В =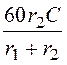==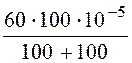 3×10 ^–4;

А =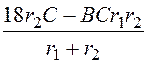==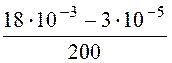 9×10 ^–5;

D = 10r₂C – АСr₁r₂ = 0,01 – 9×10 ^–5×10 ^–5×10 ⁴ = 0,01.

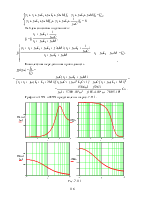
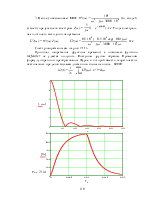
Окончательно получаем:

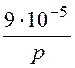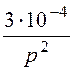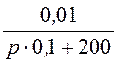
I₃(p) =++ 9×10 ^–5 + 3×10 ^–4×t + 0,1×е ^-2000tА = i₃(t).

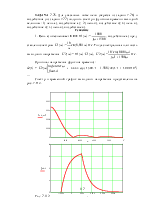
Решение

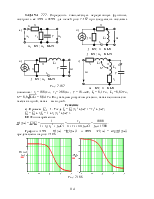
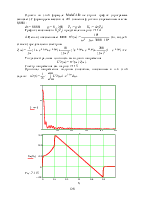
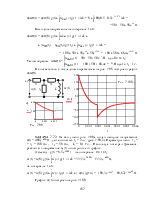
1. Рассчитаем независимое начальное условие и запишем величину внутренней операторной ЭДС:   i_L(0₊) = i_L(0_-) === 2,4 А,

Li_L(0₊) = 0,25·2,4 = 0,6 В·с.

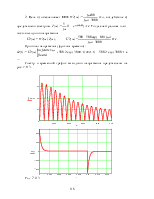
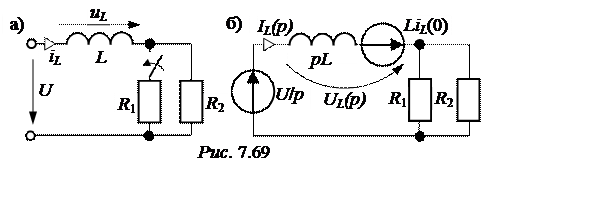
2. Эквивалентная операторная схема приведена на рис. 7.69,б.

3. Поскольку обе операторные ЭДС оказались в одной ветви, изображе-ние тока I_L(p) определим по закону Ома: