Для выполнения операций преобразования Лапласа в среде MathCAD запишем мгновенное значение тока одной формулой, используя скачкообразную единичную функцию (функцию Хевисайда) 1(t), которая в MathCAD обозначается как Ф(t): J(t) : = 0.05·(Ф(t) – Ф(t–t)).
Изображение тока источника:
J(s) : = J(t) 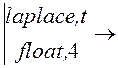
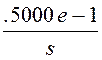 –
.5000е-1·
–
.5000е-1·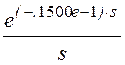 , то есть J(р) =
, то есть J(р) =![]() (1 – е -pt).
(1 – е -pt).
Спектральная плотность
тока источника может быть получена из изображения тока заменой р на jw:
J(w) :=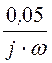 (1 – е –j·w·t).
(1 – е –j·w·t).
Спектральная плотность выходного напряжения находится через комплексное передаточное сопротивление:u2(w) := Z(w)·J(w).
Наконец, с помощью
системы MathCAD выполняем вычисление интеграла
обратного преобразования Фурье: u2(t) =![]() ·
·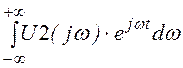 .
.
Поскольку вычисление несобственных интегралов в системе MathCAD не предусмотрено (ввиду численного решения задаваемого интеграла), то вместо бесконечных пределов возьмём достаточно большие конечные, например, 60000, допуская тем самым не слишком большую ошибку:
u2(t)
:=![]() ·
·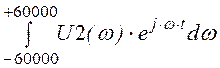 .
.
Для любого значения времени можно получить ответ. Например,
u2(0.005) = 17.717 u2(0.01) = 30.386 u2(0.05) = 2.113.
Наконец, напряжение u2(t) в виде графика можно получить, используя встроенную в MathCAD функцию invfourier:
u2(t) :=u2(w)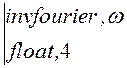 ®
31,24·Ф(1.·t) – 31.24·Ф[(-1).·t] – 62.49·e(-66.67)·t·…
®
31,24·Ф(1.·t) – 31.24·Ф[(-1).·t] – 62.49·e(-66.67)·t·…
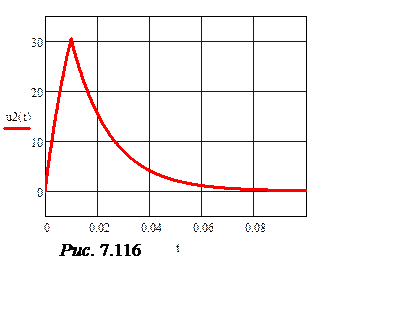 График напряжения u2(t)
приведен на рис. 7.116.
График напряжения u2(t)
приведен на рис. 7.116.
 ЗАДАЧА 7.81.
Решить задачу 7.79 с помощью интеграла Дюамеля, операторным и спектральным
методом при условии, что источник вырабатывает одиночный импульс тока, график
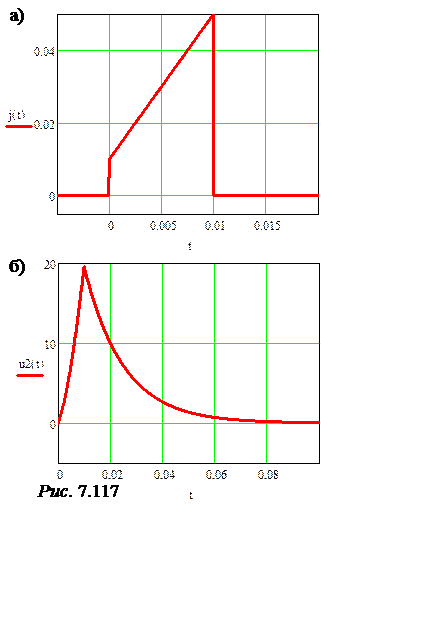
которого приведен на рис. 7.117,а. Построить график выходного напряжения.
ЗАДАЧА 7.81.
Решить задачу 7.79 с помощью интеграла Дюамеля, операторным и спектральным
методом при условии, что источник вырабатывает одиночный импульс тока, график
которого приведен на рис. 7.117,а. Построить график выходного напряжения.
Решение
1. Для решения задачи с использованием интеграла Дюамеля необходимо предварительно определить переходную характеристику (в данном случае – переходное сопротивление), которая по определению является реакцией цепи на единичное скачкообразное воздействие (функцию Хевисайда), операторное изображение которой 1/р. Другими словами, переходная характеристика численно равна выходной величине при включении цепи на единичную входную величину (в данном случае на 1 А). Определим эту переходную характеристику, используя операторное передаточное сопротивление, полученное из комплексного передаточного сопротивления заменой jwна р, путём преобразований Лапласа, которые сделаем с помощью программы MathCAD. В задаче 7.79 получено:
Z(р) =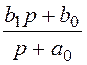 =
=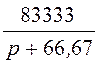 .
.
Тогда изображение выходного напряжения u2(р) := Z(р)·![]() .
.
Искомая переходная характеристика
g(t) :=u2(р)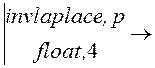 1250. – 1250.·e (-66.67)·t
1250. – 1250.·e (-66.67)·t
Импульс входного тока аналитически описывается двумя формулами:
- на интервале 0 £t£ t1 = 0,01 с j1(t) := 0.01 + 4·t;
- на интервале t1£ t j2(t) := 0.
Искомое напряжение при 0 £ t £ t1 = 0,01 с:
u21(t)
:= j1(0)·g(t) +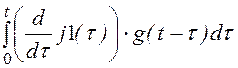
u21(t)
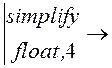 5000.·t
– 75.00 + 75.00·e (-66.67)·t.
5000.·t
– 75.00 + 75.00·e (-66.67)·t.
При t
³ t1 u22(t) := j1(0)·g(t) +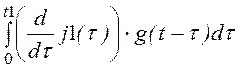 + (0 – j1(t1))·g(t
– t1)
+ (0 – j1(t1))·g(t
– t1)
u22(t) 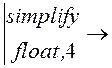 (-12.50) – 12.50·e (-66.67)·t +
.6667 + 75.00·e (-66.67)·t.
(-12.50) – 12.50·e (-66.67)·t +
.6667 + 75.00·e (-66.67)·t.
![]() Ответ записываем в
следующем виде: u2(t) := 0 if t < 0
Ответ записываем в
следующем виде: u2(t) := 0 if t < 0
u21(t) if 0 £ t £ t1
u22(t) otherwise
Таким образом, имеем следующий ответ:
u2(t) =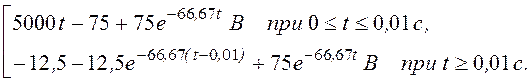
График напряжения построен на рис. 7.117,б.
2. Выполним расчёт операторным методом.
Аналитическое выражение тока источника, записанное с использованием функции Хевисайда Ф(t):
j(t) := (0.01 + 4·t)·(Ф(t) – Ф(t – t1)).
Изображение тока источника:
J(s) := j(t) 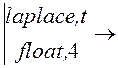
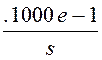 –
.5000e-1·
–
.5000e-1·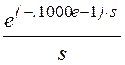 +
+![]() – 4.·
– 4.·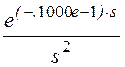 .
.
Изображение выходного напряжения: u2(р) :=Z(р)·J(р).
Оригинал выходного напряжения:
u2(t) :=u2(р) 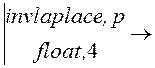 62.50·e
(-66.67)·t
– 62.50 – 12.50·Ф(t –
.1000е-1)·
62.50·e
(-66.67)·t
– 62.50 – 12.50·Ф(t –
.1000е-1)·
·e (-66.67)·t + .6667 + 62.50·Ф(t – .1000е-1) + 5000.·t – 5000.·t·Ф(t – .1000е-1).
График напряжения, построенный по последней формуле, приведен на рис. 7.117,б.
3. Выполним расчёт спектральным методом.
Оригинал и изображение тока источника:
j(t) := (0.01 + 4·t)·(Ф(t) – Ф(t – t1))
J(s) := j(t) 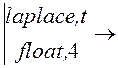
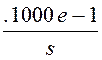 – .5000e-1·
– .5000e-1·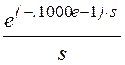 +
+![]() – 4.·
– 4.·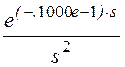 .
.
Спектральная плотность тока источника:
J(w) := 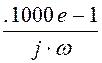 –
.5000e-1·
–
.5000e-1·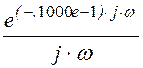 +
+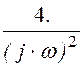 – 4.·
– 4.·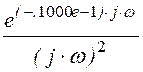 .
.
Спектральная плотность
выходного напряжения находится через комплексное передаточное сопротивление:u2(w) := Z(w)·J(w),
где комплекс-ное передаточное сопротивление Z(w) :=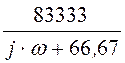 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.