Операторный метод расчёта ПП. Основные теоретические положения, страница 9

Независимые начальные условия (были найдены ранее):

i(0) = -8 А,   u_C(0) = -200 B.

Начальные значения свободных составляющих:

i_св(0) =i(0) – i_пр(0) = 4 А,   u_Cсв(0) = u_C(0) – u_Спр(0) = -133 B.

Эквивалентная операторная схема приведена на рис. 7.95,д. Расчёт выполним методом двух узлов. Изображения величин:

u_12св(р) ==;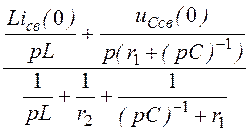

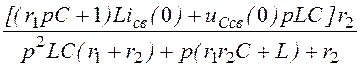I_1св(p) ===;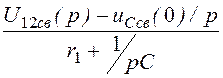

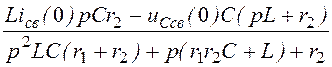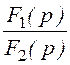i_1св(t) = 2Re=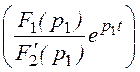

= 2Re=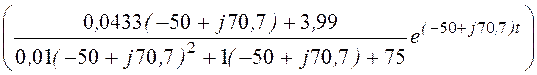

= 5,040е ^–50tsin(70,7t + 59,1°)  A,

I_2св(p) ===;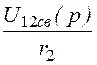

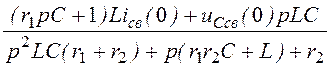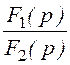i_2св(t) = 2Re=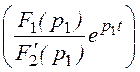

= 2Re=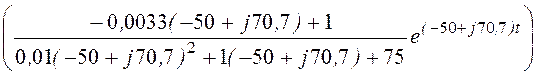

= 1,68е ^–50tsin(70,7t – 11,3°)  A.

Таким образом, поверочный расчёт даёт те же значения принуждённых и свободных составляющих токов.

ЗАДАЧА 7.70. В схеме рис. 7.96,а определить ток i₃(t), если

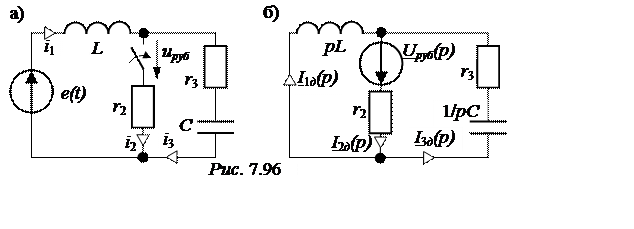e(t)= E_msin(w₀t + y),    E_m = 400 B,   w₀ = 314 рад/с,   y= -90°,

L= 0,25 Гн,   С = 400 мкФ,   r₂ = 50 Ом,   r₃ = 25 Ом.

Комментарии и ответы.  До коммутации  i₃₀(t) = 7,56sin(w₀t – 160,5°) А,

u_руб(t) = 198,4sin(w₀t – 178,2°) В.

Операторная схема при сведении расчётов к нулевым начальным условиям имеет вид рис. 7.96,б;   U_руб(p) ==;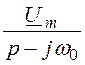

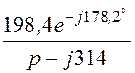I_3д(p) ==;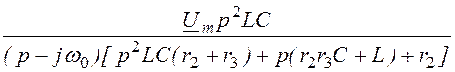

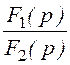i_3д(t) = 2,684sin(w₀t – 159,34°) + 0,878е ^–50tsin(64,55t + 79,7°) А,

i₃(t) = i₃₀(t) – i_3д(t) = 4,88sin(w₀t – 161,1°) – 0,878е ^–50tsin(64,55t + 79,7°) А.

7.3. РАСЧЁТ ПП МЕТОДОМ ИНТЕГРАЛА ДЮАМЕЛЯ

При подключении цепи к источнику единичного напряжения или тока реакция цепи (напряжение на любом участке или ток в любой ветви как функция времени) называется переходной функцией g(t). Если к пассивной цепи в момент  t = 0  подключается источник с воздействием   f_И(t), являю-щимся непрерывной функцией времени, то реакцию цепи f(t) определяют интегралом Дюамеля по формуле

f(t) = f_И(0)·g(t) +.

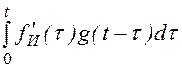Если функция воздействия имеет различные выражения на разных интервалах времени, то интервал интегрирования разбивается на отдельные участки, реакцию цепи рассчитывают для каждого интервала времени отдельно, причём на каждом интервале указанная выше конструкция интеграла Дюамеля применяется столько раз, каким по счёту является данный интервал. 

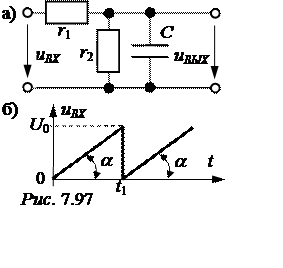
ЗАДАЧА 7.71. На вход схемы рис. 7.97,а подано напряжение u_ВХ(t)  (рис. 7.97,б). Параметры схемы: r₁ = r₂ =10 кОм, С = 200 мкФ, U₀ =100 В, t₁ =1 с.

Используя интеграл Дюамеля, рассчитать напряжение на конденсаторе, построить его кривую.

Решение

Рассчитаем переходную характеристику классическим методом. При подключении цепи рис. 7.97,а к источнику единичного напряжения имеем:

u_ВЫХпр =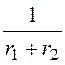r₂ = 10/(10+10) = 0,5 В,    р = -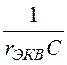= -= -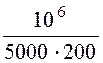1 с ^-1,

u_ВЫХ(0) = 0;     u_ВЫХ(t) = u_ВЫХпр + (u_ВЫХ(0) – u_ВЫХпр)е ^рt = 0,5 – 0,5е ^–t В, окончательно,  g(t) = 0,5 – 0,5е ^–t.

Запишем напряжение u_ВХ(t) аналитически:

u_ВХ(t) =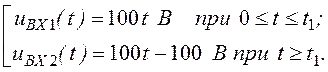

Производная от напряжения:u_ВХ ¢(t) =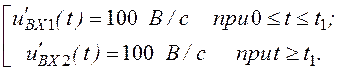

Выходное напряжение на интервале   0 £ t £t₁:

u_ВЫХ1(t) =u_ВХ1(0)·g(t) +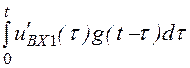= 0 +=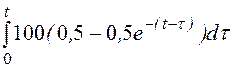

= 50t – 50 + 50е ^–t В.

Выходное напряжение на интервале  t ³t₁:

u_ВЫХ2(t) = u_ВХ1(0)·g(t) ++

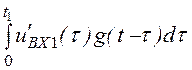+ (u_ВХ2(t₁) – u_ВХ1(t₁))g(t-t₁) +=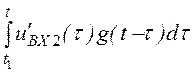

 = -100 + 50t + 50е ^–t+ 50е ^–(t-1) = -100 + 50t + 68,4е ^–(t-1) В.

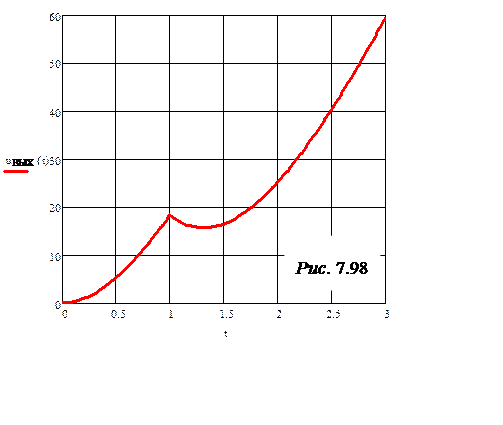
Таким образом,   u_ВЫХ(t) =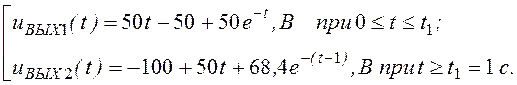

В соответствии с последним выражением на рис. 7.98 построен график u_ВЫХ(t).

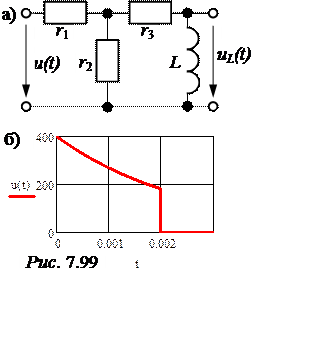
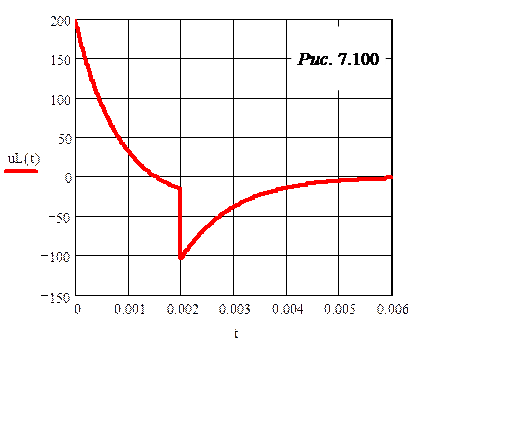
ЗАДАЧА 7.72. На вход цепи рис. 7.99,а подан импульс напряжения  u(t) = 400е ^-400t В  длительностью  t₁ = 2 мс  (рис. 7.99,б). Параметры цепи   r₁ = = r₂ = 100 Ом,   r₃ = 50 Ом,   L = 0,1 Гн.   Используя интеграл Дюамеля, рассчитать напряжение u_L(t) и построить его график.

Ответы:  g(t) = 0,5е ^-1000t,     на интервале   0 £ t £t₁:

u_L(t) = u(0)·g(t) +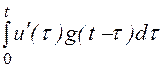= 333,3е ^-1000t – 133,3е ^-400t В, на интервале  t ³t₁:

u_L(t) = u(0)·g(t) +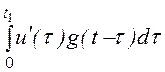+ (-u(t₁))g(t-t₁) = -109,3е ^-1000t  – 89,87е ^-1000t+2 В.

График u_L(t) построен на рис. 7.100.

ЗАДАЧА 7.73. Используя интеграл Дюамеля, рассчитать ток i₂(t)  в це-пи рис. 7.101,а при воздействии ступенчатого напряжения u(t) (рис. 7.101,б), если  r₁ = r₂ = 20 Ом,  r₃ = 10 Ом,  С = 1000 мкФ,   t₁ = 20 мс.

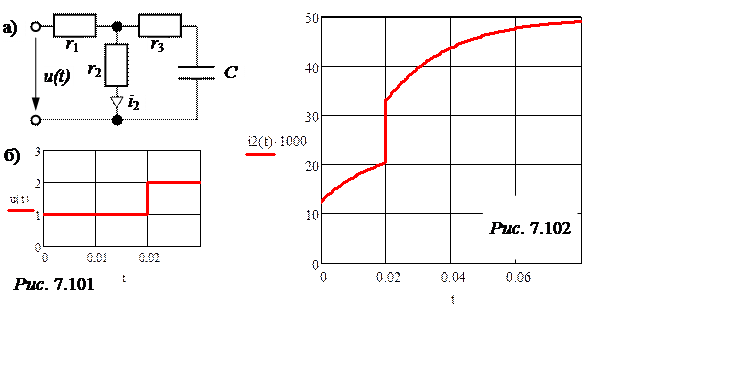Ответы:  g(t) = 25 – 12,5е ^-50t мСм,  u(t) =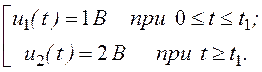

на интервале   0 £ t £ t₁:   i₂(t) = u₁(0)·g(t) = 25 – 12,5е ^-50t мА,