i2(t) = 0,784sin(w0t + 13,6°) – 0,254×е -33t+ 0,07×е -1207t A.
ЗАДАЧА 7.68. Определить ток i2(t) в схеме рис. 7.94,а:
r1 = 20 Ом, r2 = 100 Ом, L1= 0,5 Гн, L2= 0,6 Гн, M= 0,5 Гн,
 e(t)=
Emsinw0t,
Em = 100 B, w0 = 100 рад/с.
e(t)=
Emsinw0t,
Em = 100 B, w0 = 100 рад/с.
Ответы. До коммутации: i1(t) = 1,857sin(w0t – 68,2°) А.
Независимые начальные условия:i1(0) = -1,724 А, i2(0) = 0.
Принуждённые составляющие токов:
i1пр =1,828sin(w0t – 45,44°) А, i2пр = 0,784sin(w0t + 13,6°) А.
Начальные значения свободных составляющих:
i1св(0) = -0,421 А, i2св (0) = -0,1844 А.
Операторная схема для свободных составляющих на рис. 7.96,б.
Изображение и оригинал тока i2св:
I2св(p) =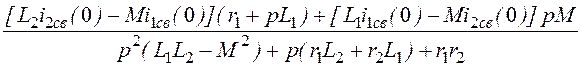 ;
;
i2св(t) = 0,0392×е -33t – 0,2236×е -1207t A.
Полный ток: i2(t) = 0,784sin(w0t + 13,6°) + 0,0392×е -33t– 0,2236×е -1207t A.
 |
Решение
Рассчитаем состояние цепи рис. 7.95,а до коммутации: i20 = 0;
I1m0 = Im0 =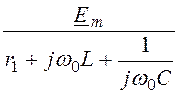 =
=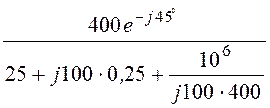 = 16·е –j45° A;
= 16·е –j45° A;
UСm0
= I1m0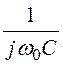 = 16·е –j45°·(-j25) = 400·е –j135°В;
= 16·е –j45°·(-j25) = 400·е –j135°В;
Uрубm = I1m0(r1 +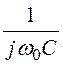 ) = 16·е –j45°·(25 – j25) = 400
) = 16·е –j45°·(25 – j25) = 400![]() ·е –j90°В;
·е –j90°В;
i0(t) = i10(t) = Im(I1m0·е jw0·t) = 16sin(w0t – 45°) A;
uС0(t) = 400sin(w0t – 135°) В; uруб(t)
= 400![]() sin(w0t – 90°) В.
sin(w0t – 90°) В.
Независимые начальные условия:
i(0+) = i(0-) = 16sin(-45°) = -8![]() А, uC(0+)
= uC(0-)
= 400sin(-135°) = -200
А, uC(0+)
= uC(0-)
= 400sin(-135°) = -200![]() B.
B.
Дальнейшие расчёты можно вести по схемам рис. 7.95,б и в.
Выполним расчёт токов ПП, используя приём сведения расчётов к нулевым начальным условиям. В этом случае в соответствии с принципом наложения искомые токи вычисляются как
i1(t) = i10(t) – i1д(t), i2(t) = i20(t) + i2д(t).
Токи дополнительного режима i1д(t)
и i2д(t)
определим операторным методом в
соответствии со схемой рис. 7.95,г. Выполним расчёт указанной схемы: uруб(р) =Uрубm·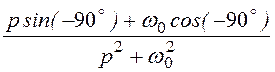 =
=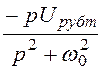 ;
;
I2д(p) =
=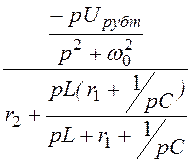 =
=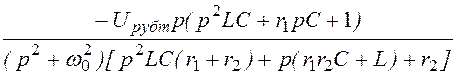 =
=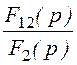 ;
;
I1д(p) = I2д(p)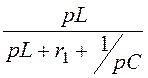 =
=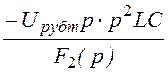 =
=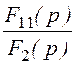 .
.
По теореме разложения определим оригиналы токов.
Корни уравнения F2(p) = 0: p1,2= ± jw0 = ±j100 с –1,
p2LC(r1 + r2) + p(r1r2C+ L) + r2 = 10 -2p2 + p
+ 75 = 0, p3,4= -50 ± j50![]() с –1.
с –1.
F2¢(p) =![]() = [2pLC(r1 + r2) +
(r1r2C + L)](p2+ w02) + 2p[p2LC(r1
+ r2) +
= [2pLC(r1 + r2) +
(r1r2C + L)](p2+ w02) + 2p[p2LC(r1
+ r2) +
+ p(r1r2C + L) + r2] = (0,02p + 1)·(p2 + 10000) + p(0,02p2 + 2p + 150),
F2¢(p1) = F ¢2(j100) = -20000 – j5000 = 20620·е –j165,96°,
F2¢(p3) = F ¢2(-50 + j50![]() ) = 10000 + j10610
= 14580·е j46,69°.
) = 10000 + j10610
= 14580·е j46,69°.
F11(p) = -Uрубm· p3·LC = -0,05656p3,
F11(p1) = j56560, F11(p3) = -35360 – j10000 = 36740·е –j164,21°,
i1д(t) = 2Re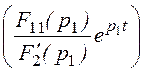 + 2Re
+ 2Re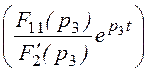 =
=
= 2Re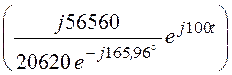 + 2Re
+ 2Re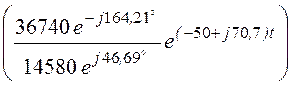 =
=
= -5,486cos(100t + 75,96°) – 5,040е –50tcos(70,7t – 30,9°) =
= -5,486sin(100t + 165,96°) – 5,040е –50tsin(70,7t + 59,1°) A.
F12(p) = -Uрубm· p(p2·LC + r1pC + 1) = -0,05656p3 – 5,656p2 – 565,6p,
F12(p1) = 56560, F12(p3) = 7071 – j10000 = 12250·е –j54,74°,
i2д(t) = 2Re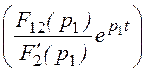 + 2Re
+ 2Re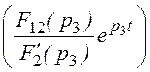 =
=
= 2Re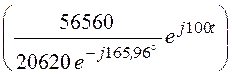 + 2Re
+ 2Re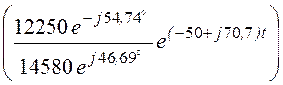 =
=
= 5,486sin(100t – 104,04°) + 1,680е –50tsin(70,7t – 11,43°) A.
Окончательно записываем полные токи:
i1(t) = 16sin(w0t – 45°) + 5,486sin(100t + 165,96°) + 5,040е –50tsin(70,7t + 59,1°) =
= 11,64sin(100t – 59,1°) + 5,040е –50tsin(70,7t + 59,1°) A,
i2(t) = i2д(t) = 5,486sin(100t – 104,04°) + 1,680е –50tsin(70,7t – 11,43°) A.
Выполним поверочный расчёт принуждённых составляющих токов сим-волическим методом, а свободных составляющих – операторным методом.
Imпр =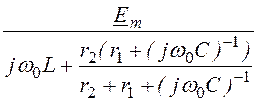 =
=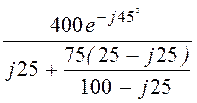 = 16·е –j73,05° A;
= 16·е –j73,05° A;
I1mпр = Imпр·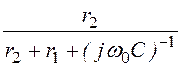 = 16·е –j73,05°·
= 16·е –j73,05°·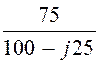 = 11,65·е
–j59° A;
= 11,65·е
–j59° A;
I2mпр = Imпр·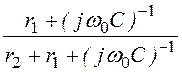 = 16·е –j73,05°·
= 16·е –j73,05°·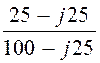 = 5,49·е
–j104°
A;
= 5,49·е
–j104°
A;
UСmпр = I1mnp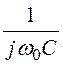 = 11,65·е –j59°·(-j25) = 291,4·е –j149°В;
= 11,65·е –j59°·(-j25) = 291,4·е –j149°В;
iпр(t) = 16sin(w0t – 73,05°) A, uСпр(t) = 291,4sin(w0t – 149°) В,
iпр(0) = 16sin(-73,05°) = -15,3 A, uСпр(0) = 291,4sin(-149°) = -150 В,
i1пр(t) = 11,65sin(w0t – 59°) A, i2пр(t) = 5,49sin(w0t – 104°) A.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.