Операторный метод расчёта ПП. Основные теоретические положения, страница 3

i(t) = i_пр(t) + i_св(t) = 0,707×sin(200t + 135°) – 0,3×e ^-200t A.

ii. Расчёт операторным методом.

1. Независимое начальное условие –

u_C(0₊) = u_C(0_-) = 80 B.

2. Эквивалентная операторная схема на рис. 7.75.

Изображение напряжения источника находим по прямому преобразованию Лапласа:

u(t) = 100×sin(200t+ 90°) 100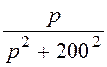= u(p).

3. Изображение тока находим по закону Ома, причём с целью получения выражений, соответствующих таблице преобразований Лапласа, полученное выражение разложим на правильные дроби:

I(p) ====

=+=.

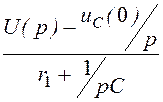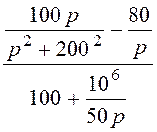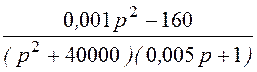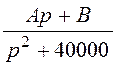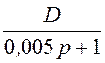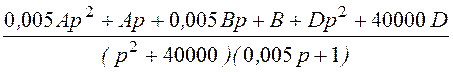Возникает следующая система уравнений:     0,005А + D = 0,001,

A+ 0,005B = 0,

B+ 40000D = -160.

Решение системы:   А = 0,5;     B= -100;     D = -0,0015.

Таким образом,

I(p) =+=+.

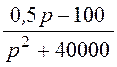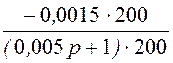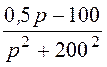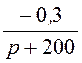Первую дробь приведём к следующему табличному виду:

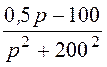= М.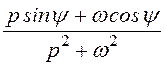

Возникает ещё одна система уравнений:

Мsiny = 0,5,                    Мsiny = 0,5,         

200×Мcosy = -100.          Мcosy = -0,5.

tgy = -1,     y = 135°,     М =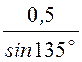= 0,707.

4. По таблице преобразований Лапласа находим ответ:

i(t) = 0,707×sin(200t+ 135°) – 0,3×e ^-200t A.

iii. Следует отметить, что при синусоидальном источнике, напряжение или ток которого можно записать в комплексной форме, возможен и другой подход к нахождению изображений и оригиналов величин. Покажем его.

Согласно символическому методу, синусоидальное напряжение равно мнимой части от комплексного мгновенного значения, записываемого в виде экспоненты. Но тогда и изображение напряжения источника может быть получено взятием мнимой части от изображения комплексного мгновенного значения:

u(t) = U_m×sin(wt+y_u)= Im[U_m×e ^{j(wt + yu)}]= Im[U_me ^jyu×e ^jwt] Im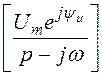= U(p).

Изображение тока находим по закону Ома по схеме рис. 7.75:

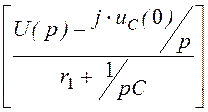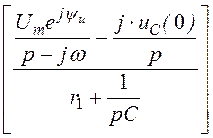I(p) = Im= Im=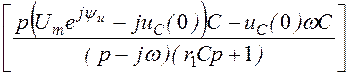

= Im=  Im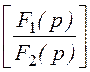, где F₁(p) = pC(U_me ^jyu – ju_C(0)) – u_C(0)wC,

F₂(p) = (p– jw)(r₁Cp + 1).

Оригинал тока найдём с помощью теоремы разложения. Для этого предварительно вычислим:

- корни уравнения  F₂(p) = 0:   p₁ = jw= j200 с ^–1;    p₂ = -= -200 с ^–1;

-  F₂¢(p) = 2r₁Cp + 1 – jwr₁C;   F₂¢(p₁) = j + 1;   F₂¢(p₂) = -1 – j;

-  F₁(p₁) = U_me ^jyujwC = 100×j×j×200×50×10 ^–6 = -1;

-  F₁(p₂) = -200(100j – j80)×50×10 ^–6 – 80×200×50×10 ^–6 =

= -0,8 – j0,2 = 0,825×e ^–j166°.

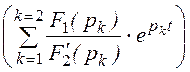i(t) = Im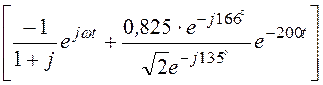= Im=

= Im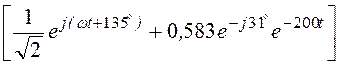=×sin(wt +135°) – 0,583sin31°×e ^-200t =

= 0,707×sin(200t+ 135°) – 0,3×e ^-200t A.

iV. Наконец, операторным методом можно рассчитать только свободные составляющие тока и напряжения на конденсаторе, предварительно рассчитав принуждённые составляющие символическим методом (см. часть i настоящей задачи):   i_пр(t) = 0,707×sin(200t+ 135°) A;

u_Cпр(t) = 70,7×sin(200t + 45°) B,

u_Cпр(0) = 70,7×sin45° = 50 B,    u_Cсв(0) = u_C(0) – u_Cпр(0) = 80 – 50 = 30 B.

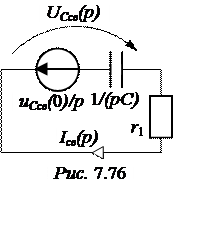
Эквивалентная операторная схема для свободного режима представлена на рис. 7.76.

Полученная цепь рассчитывается на основании закона Ома, оригиналы величин находим, используя таблицу преобразований Лапласа.

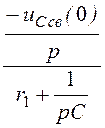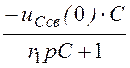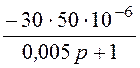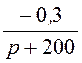
I_св(p)====-0,3×e ^-200t A = i_св(t);

u_Cсв(p) = I_св(p)×+ =+ =

====

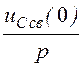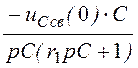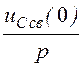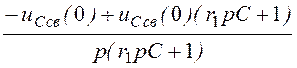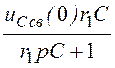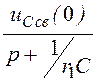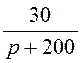
= 30×e ^-200t В = u_Cсв(t).

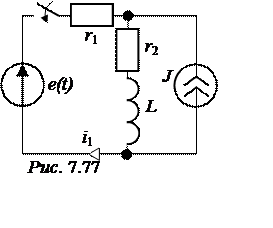ЗАДАЧА 7.52. В схеме рис. 7.77 найти ток i₁(t), если   e(t) = 100sin(1000t – 15°) В,

r₁= r₂= 25 Ом,   L = 0,1 Гн,   J = 4 A.

Ответы.   I₁(p) =;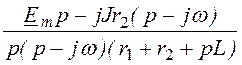

i₁(t) = -2 + 2sin(1000t – 78,5°) + 3,96e ^-500t A.

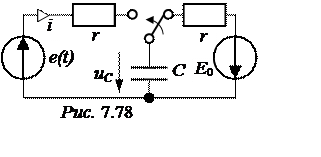Задача 7.53. В схеме рис. 7.78

r = 100 Ом,  С = 10 мкФ,   E₀ = 300 В,

e(t) = 100sin(1000t – 90°) В.

Определить ток ПП.

Ответы. u_С(0) = -300 В, расчётная операторная схема идентична схеме рис. 7.75;

e(t) = -E_mcosw₀t ;

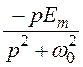I(p) ===;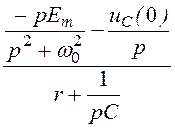

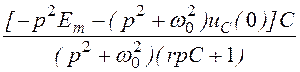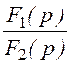p_1,2 = ± jw₀ = ± j1000 c ^-1,   p₃ = -1/(rC) = -1000 c ^-1;

F₂¢(p) = 2p(rpC + 1) + (p² + w₀²)rC;

i(t) =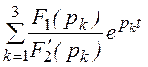= 2Re+=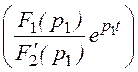

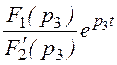=cos(1000t – 135°) + 2,5e ^-1000t = 0,707sin(1000t – 45°) + 2,5e ^-1000t A.

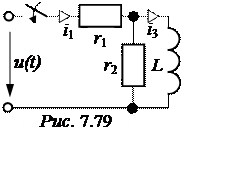
ЗАДАЧА 7.54. В схеме рис. 7.79 рассчитать токи i₁(t) и i₃(t), если   u(t) = U₀·e ^-at,  U₀ = 40 В,

a = 20 c ^-1,   r₁= 5 Ом,  r₂= 10 Ом,   L= 100 мГн.

Ответы. U(p) =;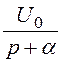

I₁(p) ===;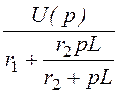

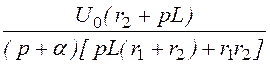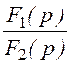p₁= -a = -20 c ^-1;   p₂ =-33,33 c ^-1;   F₂¢(p) = (р+ a)L(r₁+ r₂) + рL(r₁+ r₂) + r₁·r₂;

i₁(t) =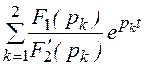= 16e ^-20t – 13,33e ^-33,33t A;

I₃(p) = I₁(p)·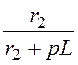=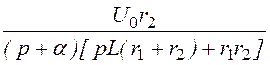;   i₃(t) = 20e ^-20t – 20e ^-33,33t A.