Операторный метод расчёта ПП. Основные теоретические положения, страница 2

I_L(p) =====

==.

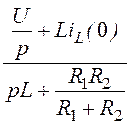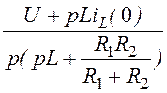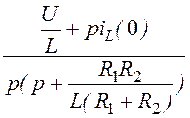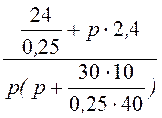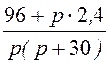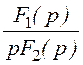На основании второго закона Кирхгофа

U_L(p) = рL·I_L(p) – Li_L(0) = рL·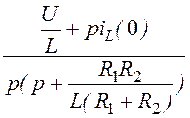– Li_L(0) =

===.

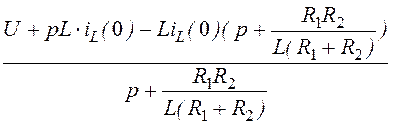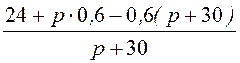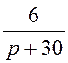4. Оригинал тока  i_L(t) определим с помощью теоремы разложения:

i_L(t) =+.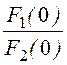

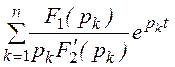Корень уравнения   F₂(p) = p + 30 = 0   –     p = -30 c ^-1, производная   F₂¢(p) = 1,   F₂(0) = 30;

F₁(0) = 96,   F₁(p) = 96 – 30·2,4 = 24;

i_L(t) =+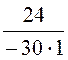е ^-30t= 3,2 – 0,8е ^-30t А.

Изображение напряжения на индуктивности  U_L(p) =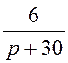 есть стан-дартная (табличная) функция. Это – изображение экспоненты, поэтому

u_L(t) =6е ^-30tB.

Задача7.47. В схеме рис. 7.70,а рассчитать ток i₂(t) и напряжение на ёмкости u_С(t), если  u = 240 В,  Е₃ = 100 В,  r₁ = r₃ = 50 Ом,  С = 1000 мкФ.

Решение

1. Независимое начальное условие:      u_С(0₊) = u_С(0_-) = -Е₃ = -100 В.

Внутренняя операторная ЭДС  = -.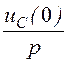

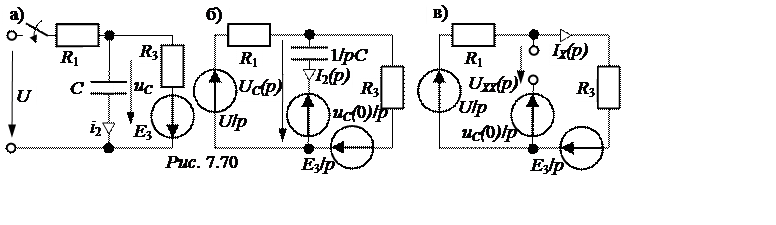
2. Операторная схема замещения представлена на рис. 7.70,б.

3. Поскольку по условию задачи требуется рассчитать только один ток, то его изображение определим методом эквивалентного генератора          (рис. 7.70,в). По второму закону Кирхгофа:

U_ХХ(р) + r₁·I_Х(р) = – ==.

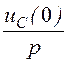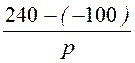По закону Ома   I_Х(р) ===.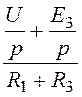

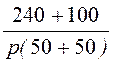Тогда  U_ХХ(р) = – 50=.

Входное сопротивление схемы относительно разомкнутых зажимов

Z_BХ(р) =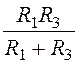==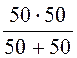 25 Ом.

Изображение искомого токаI₂(p):

I₂(p) ===.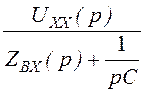

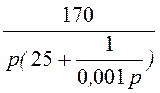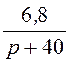На основании второго закона Кирхгофа  U_С(р) –I₂(p) =.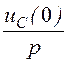

Отсюда      U_С(р) =+·==.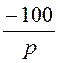

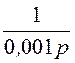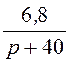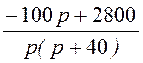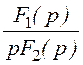4. Оригинал тока найдём по таблице преобразований Лапласа:

i₂(t) = 6,8е ^-40t А.

Оригинал напряжения найдём с помощью теоремы разложения:

корень уравнения   F₂(p) = p + 40 = 0   –     p = -40 c ^-1,

производная   F₂¢(p) = 1,   F₂(0) = 40;

F₁(0) = 2800,   F₁(p) = -100·(-40) + 2800 = 6800;

u_С(t) =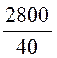+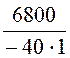е ^-40t= 70 – 170е ^-40t В.

ЗАДАЧА 7.48. Решить задачу 7.11 операторным методом.

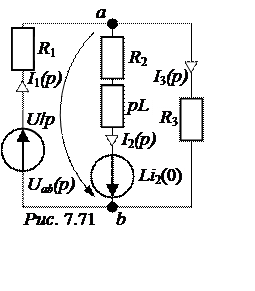
Ответы:  i₂(0) = 0,8 A; эквивалентная опера-торная схема на рис. 7.71;

U_ab(p) =;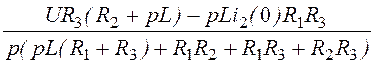

I₁(p) ==;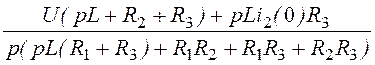

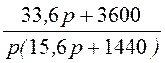I₂(p) ==;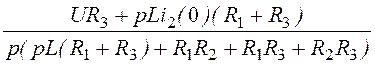

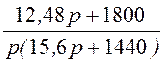I₃(p) ==;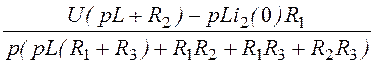

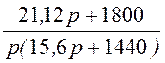i₁(t) = 2,5 – 0,346е ^-92,31t А;  i₂(t) = 1,25 – 0,45е ^-92,31t А;   i₃(t) = 1,25 + 0,104е ^-92,31t А.

Задача 7.49. Решить задачу 7.12 операторным методом.

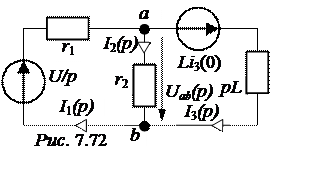Ответы:  независимое начальное условие – i₃(0) = 1 А, эквивалентная опера-торная схема представлена на рис. 7.72; выражения для узлового напряжения и токов:U_ab(p) =;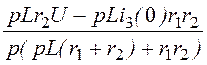

I₁(p) =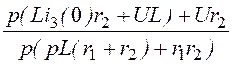 i₁(t) = 3 – 1×е ^-100t А;

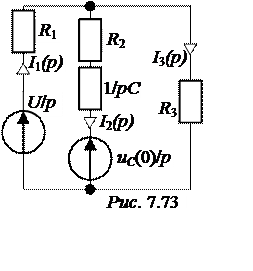I₂(p) =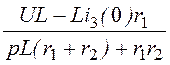 i₂(t) = е ^-100t А;

I₃(p) =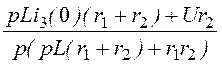 i₃(t) = 3 – 2×е ^-100t А.

Задача7.50. Решить задачу 7.13 опера-торным методом.

Ответы: u_С(0) = 100 B, эквивалентная опера-торная схема на рис. 7.73;

I₁(p) ==;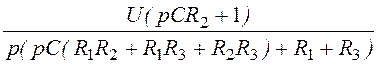

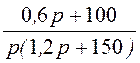I₂(p) ==;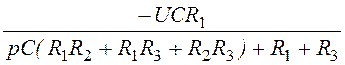

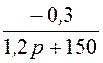I₃(p) ==;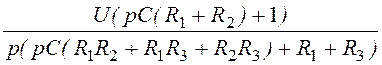

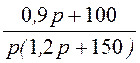i₁(t) = 0,667 – 0,167е ^-125t А;      i₂(t) = -0,25е ^-125t А;     i₃(t) = 0,667 + 0,083е ^-125t А.

ЗАДАЧА 7.51. Рассчитать переходный про-цесс в схеме рис. 7.74 классическим и операторным методами:  u(t) = 100×sin(200t+ 90°) B,

r₁ = r₂ = 100 Ом,   С = 50 мкФ.

Решение

I. Расчёт классическим методом.

1. Получим независимое начальное условие  u_C(0) анализом цепи до коммутации:

х_C ===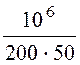 100 Ом,  Z =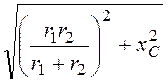==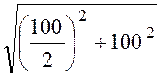 111,8 Ом,

I_m ===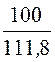 0,894 A,     U_Cm = I_m×х_C = 0,894×100 = 89,4 B,

j  = arctg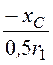= -arctg= -63,4°,     y_i =y_u – j= 90° + 63,4°  = 153,4°,

y_uC = y_i – 90° = 153,4° – 90° = 63,4°,

u_C(t_-) = 89,4×sin(200t + 63,4°) B,   u_C(0₊) = u_C(0_-) = 89,4×sin63,4° = 80 B.

Зависимое начальное условие (ток в цепи в момент сразу после коммутации):   i(0) =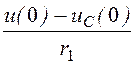==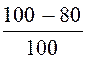 0,2 А.

2. Рассчитаем принуждённые составляющие тока и напряжения на конденсаторе:

I_mпр =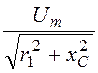==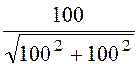 0,707 A,     U_Cmпр = I_mпр×х_C = 0,707×100 = 70,7 B,

y_iпр =y_u – arctg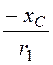= 90° + arctg= 135°,

y_uCпр = y_iпр – 90° = 135° – 90° = 45°,

u_Cпр(t) = 70,7×sin(200t + 45°) B,     i_пр(t) = 0,707×sin(200t + 135°) A.

Начальные значения принуждённых составляющих:

u_Cпр(0) = 70,7×sin45° = 50 B,     i_пр(0) = 0,707×sin135° = 0,5 A.

3. Характеристическое уравнение и его корень:

+ r₁ = 0,      р = -= -= -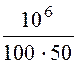200 с ^-1.

4. Свободные составляющие:  u_Cсв(t) = A×e ^рt,   i_св(t) = В×e ^рt.

Постоянные интегрирования:

A = u_Cсв(0) = u_C(0) – u_Cпр(0) = 80 – 50 = 30,

В = i_св(0) = i(0) – i_пр(0) = 0,2 – 0,5 = -0,3.

5. Окончательно получаем:

u_C(t) = u_Cпр(t) + u_Cсв(t) = 70,7×sin(200t + 45°) + 30×e ^-200t B,