Операторный метод расчёта ПП. Основные теоретические положения, страница 6

5. Оригинал тока i_2св(t) определим с помощью теоремы разложения.

Корни уравнения   F₂(p) = 0,01p² + p+ 75 = 0     р_1,2 = -50 ± j50 c ^-1;

F₂¢(p) = 0,02p + 1;    F₂¢(p₁) = j.

F₁(p₁) = (10 ^-2·(-50 + j50)+1)·0,25·4 + 10 ^-4·(-50+j50)·(-133) = 1,188·e ^–j11,3°;

i_2св(t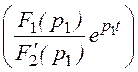) = 2Re= 2Re=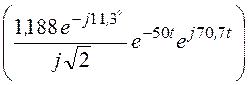

= 1,68e ^-50tcos(70,7t – 101,3°) = 1,68e ^-50tsin(70,7t – 11,3°)А.

Окончательно получаем:

i₂(t) = i_2пр(t) + i_2св(t) = 5,49sin(100t – 104°)+ 1,68e ^-50tsin(70,7t – 11,3°)А.

ЗАДАЧА 7.60. В схеме рис. 7.85,а рассчитать токи переходного процесса операторным методом. Параметры цепи:

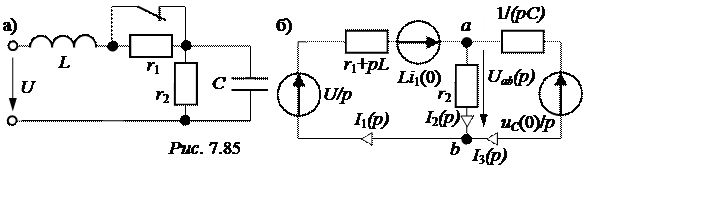U= 200 В,   r₁ = 40 Ом,   r₂ = 60 Ом,   L= 0,7 Гн,   С = 100 мкФ.

Ответы: независимые начальные условия –  i₁(0) = 3,33 А, u_C(0) = 200 В,  эквивалентная операторная схема представлена на рис. 7.85,б; изображения узлового напряжения и токов:

U_ab(p) =;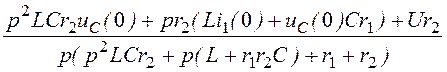

I₁(p) =;

I₂(p) =;

I₃(p) =;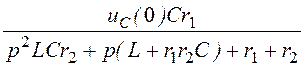

оригиналы токов:   i₁(t) = 2 + 1,39×е ^–111,9tsin(106,2t + 106,3°) A;

i₂(t) = 2 + 1,936×е ^–111,9tsin(106,2t + 43,5°) A;     i₃(t) = 1,794×е ^–111,9tsin(106,2t) A.

ЗАДАЧА 7.61. Решить задачу 7.32 операторным методом.

Решение

1. Независимые начальные условия:

i₁(0₊) = i₁(0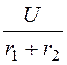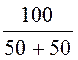_-) === 1 А,   i₃(0₊) = i₃(0_-) = 0.

2. Эквивалентная операторная схема представлена на рис. 7.86.

3. Расчёт цепи выполним методом контурных токов. Система уравнений для контурных токов (в качестве контурных приняты токи первой и третьей ветвей) имеет вид:

I₁(р)(r₁+ pL₁+ r₂) + I₃(р)(pМ– r₂) = + L₁i₁(0),

I₁(р)(pМ– r₂) + I₃(р)(pL₂+ r₂) = Mi₁(0).

Решим систему методом Крамера:

D(р) =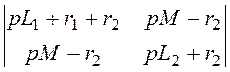= p²(L₁L₂ – М²) + p((L₁ + 2M)r₂+ L₂(r₁+ r₂)) + r₁r₂;

D₁(р) ==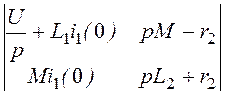

=(p²(L₁L₂ – М²)i₁(0) + p(Mi₁(0)r₂ + UL₂ + L₁i₁(0)r₂) + Ur₂);

D₃(р) =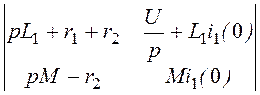={p[i₁(0)(L₁r₂ + M(r₁ + r₂)) – UM] + Ur₂};

I₁(р)===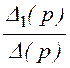

==;

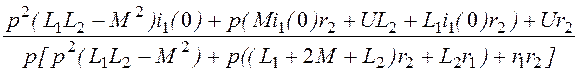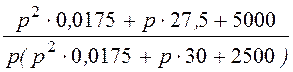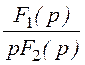I₃(р)===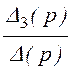

==.

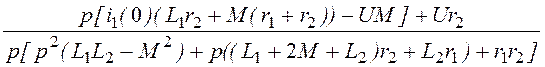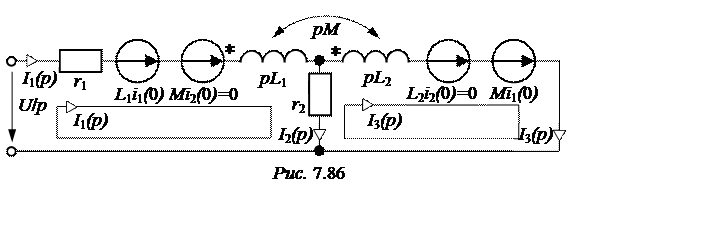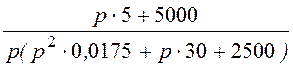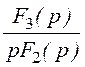4. Оригиналы токов определим с помощью теоремы разложения.

Корни уравнения  F₂(р) = p²×0,0175 + p×30 + 2500 = 0:

p_1,2 = -857,1 ± 769,3 c ^–1;    p₁ = -87,8 c ^–1;    p₂ = -1626,4 c ^–1.

F₂(0) = 2500;    F₂¢(p) = 0,035×p + 30;    F₂¢(p₁) = 26,93;    F₂¢(p₂) = -26,93.

Расчёт первого тока:   F₁(р) = p²×0,0175 + p×27,5+ 5000;

F₁(0) = 5000;    F₁(р₁) = 2720;   F₁(р₂) = 6565.

i₁(t) =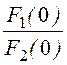+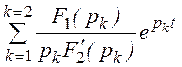=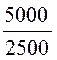+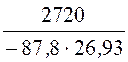×е ^–87,8t  +

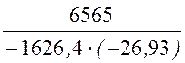+×е ^–1626,4t = 2 – 1,150×е ^–87,8t  + 0,150×е ^–1626,4t А.

Расчёт третьего тока:   F₃(р) = p×5+ 5000;

F₃(0) = 5000;    F₃(р₁) = 4561;   F₃(р₂) = -3132.

i₃(t) =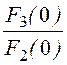+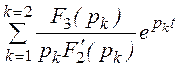=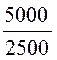+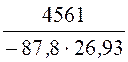×е ^–87,8t  +

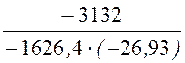+×е ^–1626,4t = 2 – 1,929×е ^–87,8t  – 0,072×е ^–1626,4t А.   

Ток второй ветви вычислим по первому закону Кирхгофа:

i₂(t) = i₁(t)– i₃(t) = 2 – 1,150×е ^–87,5t + 0,150×е ^–1626,4t – 2 + 1,929×е ^–87,8t +

+ 0,072×е ^–1626,4t = 0,779×е ^–87,8t + 0,222×е ^–1626,4t А.

ЗАДАЧА 7.62. В схеме рис. 7.87,а определить i(t), u_C(t) операторным методом,  если:  U = 100 В,   r = 200 Ом,   L= 1 Гн,   С = 100 мкФ.

Решение

1. Независимые начальные условия:

u_С(0₊) = u_С(0_-) = 0,         i(0₊) = i(0_-) = U/r = 100/200 = 0,5 A.

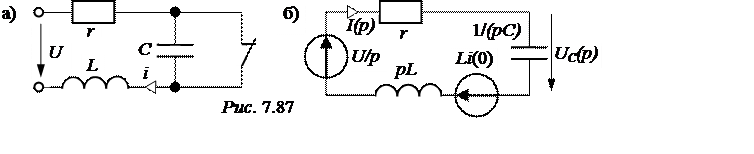
2. Эквивалентная операторная схема на рис. 7.87,б.

3. Изображения тока и напряжения на конденсаторе:

I(р) ===;

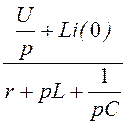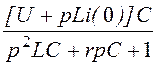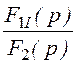U_C(р) = I(р)·==.

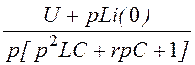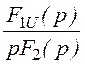4. Оригиналы величин определим с помощью теоремы разложения.

Корни уравнения  F₂(р) = p²×10 ^-4 + p×0,02 + 1 = 0:

p_1,2 =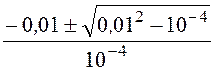= -100 ± 0 c ^–1;    p₁ = p₂ = p_k = -100 c ^–1.

При кратных корнях  p_k  кратности  m= 2  получим:

i(t) =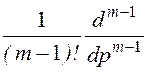[I(р)(р– p_k)^mе ^pt]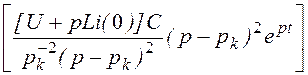_p®pk =

= _p®pk=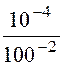[Li(0)е ^pk·t+ (U + р_kLi(0))tе ^pk·t] =

= 0,5е ^-100t + (100 – 100·1·0,5)tе ^-100t = 0,5е ^-100t + 50tе ^-100t A;

u_С(t) =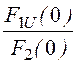+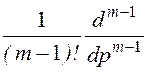[U_C(р)(р– p_k)^mе ^pt]_p®pk =

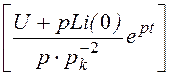=+_p®pk =

= U +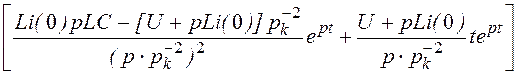 _p®pk =

= 100 – 100е ^-100t – 15000tе ^-100tВ.

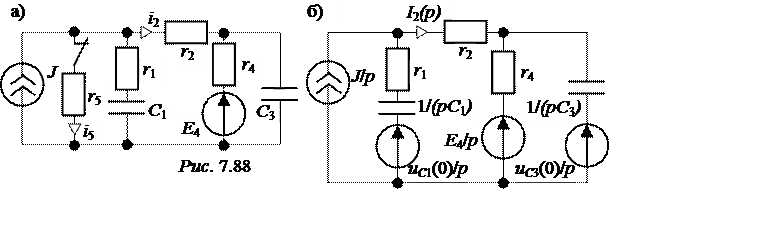
ЗАДАЧА 7.63. Определить ток ПП i₂(t) в схеме рис. 7.88,а с параметра-ми   r₁ = r₄ = 200 Ом,   r₂ = r₅ = 100 Ом,   С₁ = С₃ = 100 мкФ,   Е₄ = 300 В,   J = 1 А.

Решение