Операторный метод расчёта ПП. Основные теоретические положения, страница 10

при  t ³t₁:i₂(t) = u₁(0)·g(t) + (u₂(t₁) – u₁(t₁))g(t-t₁) = 50 – 12,5е ^-50t –12,5е ^-50t+1 мА.

График i₂(t) построен на рис. 7.102.

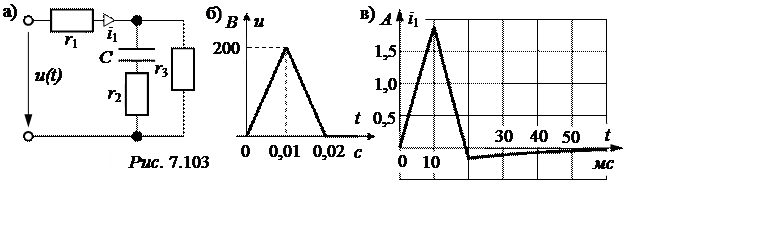
ЗАДАЧА 7.74. В схеме рис. 7.103,а рассчитать ток в резисторе r₁. Параметры цепи:  r₁ = 50 Ом,   r₂ = r₃ = 100 Ом,   С = 200 мкФ.   Напряжение источника задано графиком рис. 7.103,б. Использовать интеграл Дюамеля.

Ответы:  g(t) = 0,00667 + 0,00333×e ^–37,5t См,

i₁(t) =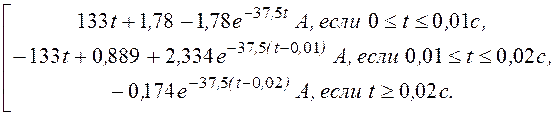

График тока на рис. 7.103,в.

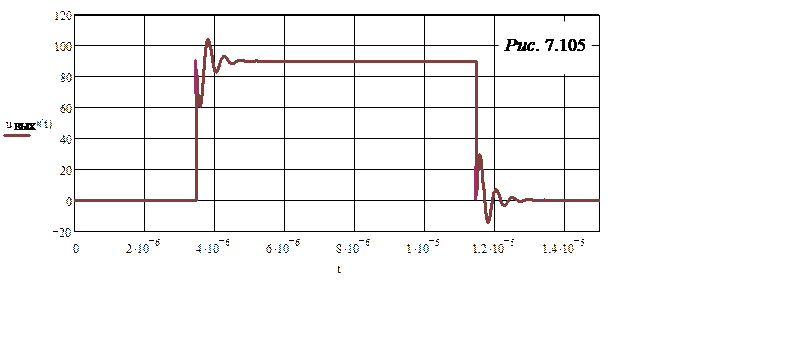
ЗАДАЧА 7.75. На рис. 7.104,а приведена схема колебательного звена системы автоматического регулирования с параметрами:  r = 115 кОм,     L = = 3,7 мГн,  С = 1,4 пФ. Определить напряжение на выходе u_ВЫХ(t) при воздей-ствии на входе прямоугольного импульса u(t) (рис. 7.104,б) с параметрами:

U₀ = 90 В (высота),  t₁ = 3,5 мкс (смещение), Т = 8 мкс (длительность). Решить задачу с помощью интеграла Дюамеля.

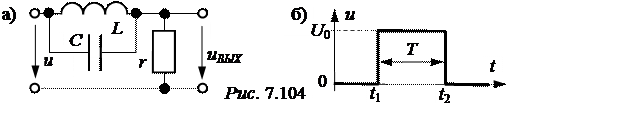Комментарии и ответы.

Передаточная функция звена: Н(p) ==.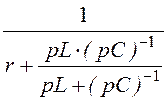

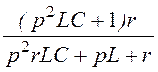Изображение и оригинал переходной функции:

G(p) =Н(p) ==;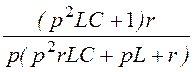

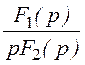g(t) =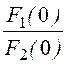+ 2Re=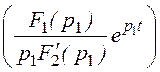

= 1 + 2Re=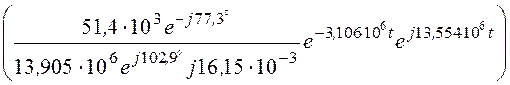

= 1 – 0,458e ^–btsin(w₀t).

Здесь  b = 3,106·10⁶ c ^-1,    w₀ = 13,554·10⁶ рад/с.

Интегралы Дюамеля вычислим с помощью системы MathCAD.

t1 := 3.5·10 ^-6      t2 := 11.5·10 ^-6     b := 3.106·10⁶   w0 := 13.554·10⁶

g(t) := 1 – 0.458·e ^–b·t·sin(w0·t)

Напряжение источника     u1(t) := 0    u2(t) := 90     u3(t) := 0

u(t) :=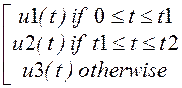

Интервал 0 £ t £ t₁:   uВЫХ1(t) := u1(0)·g(t) +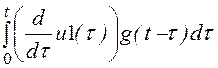

uВЫХ1(t) 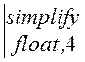 ® 0

Интервал t₁£ t £ t₂:j1(t) := u1(0)·g(t) +

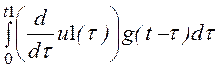
uВЫХ2(t) := j1(t) + ((u2(t1) – u1(t1))·g(t-t1) +

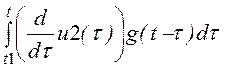
uВЫХ2(t) 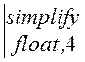 ® 90. – 41.22·e^{(-.3106e7)·t+10.87}·sin(.1355e8·t – 47.44)

или    u_ВЫХ2(t) = 90 – 41,22e ^-b(t-t1)·sin(w₀(t – t₁)).

Интервал t ³ t₂:      j2(t) := ((u2(t1) – u1(t1))·g(t-t1) +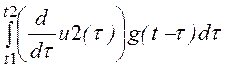

uВЫХ3(t) := j1(t) + j2(t) + ((u3(t2) – u2(t2))·g(t-t2) +

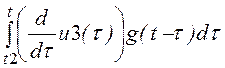
uВЫХ3(t)  ® (-41.22)·e^{(-.3106e7)·t+10.87}·sin(.1355e8·t – 47.44) +

+ 41.22·e^{(-.3106e7)·t+35.72}·sin(.1355e8·t – 155.9)

или    u_ВЫХ3(t) = -41,22e ^-b(t-t1)·sin(w₀(t – t₁)) + 41,22e ^-b(t-t2)·sin(w₀(t – t₂)).

Окончательно записываем:     uВЫХ(t) :=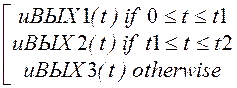

График напряжения u_ВЫХ(t) построен на рис. 7.105.

7.4. СПЕКТРАЛЬНЫЙ МЕТОД АНАЛИЗА пп

Спектральный метод применяется для определения реакции цепи (обычно это – одна выходная величина, некоторый ток или напряжение) на воздействие (входная величина) в виде импульса или серии импульсов. Эта реакция представляет собой некоторый переходный процесс. Суть метода заключается в том, что импульс воздействия представляют в виде суммы бесконечного числа (в виде интеграла) бесконечно малых по амплитуде синусоидальных функций времени, имеющих разные амплитуды, частоты и начальные фазы. Анализ процессов спектральным методом выполняют с помощью прямого (*) и обратного (**) преобразования Фурье:

F(jw) = F(w)·e ^jY(w) =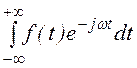,   (*)         f(t) =.    (**)

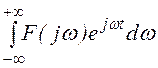Здесь функция времени (сигнал) f(t) – оригинал, изображение F(jw) – спектральная характеристика или спектральная плотность сигнала, F(w) – амплитудно-частотная, а Y(w) – фазо-частотная характеристики.

В случаях, когда функция f(t) отлична от нуля только в интервале  t > 0, прямое преобразование Фурье называют односторонним, которое является частным случаем преобразования Лапласа, в котором комплексная перемен-ная р заменена мнимой переменной jw:       F(jw) =.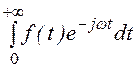

Спектральный метод анализа процессов в цепях включает в себя: определение спектральной плотности сигнала воздействия (входной величины) по заданной функции времени; определение комплексной передаточной функции цепи (частотных характеристик цепи);  определение спектральной плотности выходной величины (реакции или отклика цепи); определение выходной величины в функции времени.

Ввиду необходимости выполнения сложных и громоздких вычислений даже в сравнительно простых случаях этот метод становится целесообразным в случае применения мощной вычислительной техники. Поэтому решение ряда задач выполнено с применением системы MathCAD.