Заметим, что полученное выражение справедливо для любого (n+1)-го импульса при n ® ¥, 0 < t < ¥, если t отсчитывается от начала этого импульса, что непосредственно следует из определения оригинала: f(t) º 0 при t < 0.
Из классического метода расчёта переходных процессов следует, что i = iпр + iсв, слагаемое iпр определяется видом приложенного к схеме напряжения: если это напряжение периодическое, то уже на интервале действия первого импульса есть слагаемое iпр = iуст – установившаяся реакция на периодическое воздействие. Таким образом, iуст = i(1) – iсв, где i(1) – ток переходного процесса в интервале действия первого импульса.
Для рассматриваемого примера в интервале действия (n+1)-го импульса для t(0 … t0) получаем
iуст(t) = Imsin(wt – j) + Imsinj ·
– Imsinj 
=
= Imsin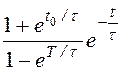(wt – j) – Imsinj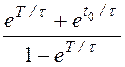 
= 4,94sin(w t – 85,45º) + 22,24 A;
в период паузы t(t0 … T)
iуст(t) = A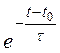
– Imsinj =
=
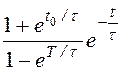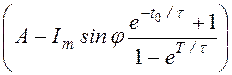
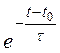= 22,24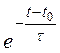 A.
Как и следовало ожидать, полученные результаты совпадают с ранее вычисленными двумя разными методами. Отметим, что для контроля правильности решения задачи для периодического решения необходимо проверять условие, на котором базируется первый из рассмотренных методов: iуст(0) = iуст(T).
7.2.3. ПП в цепях с двумя накопителями
 |
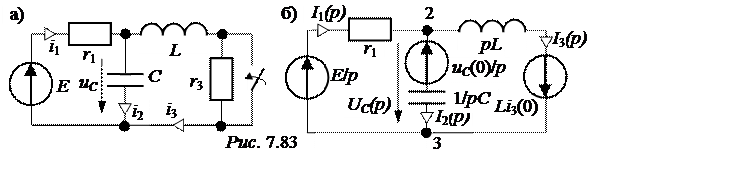Е = 300 В, r1 = r3 = 25 Ом, L= 0,02 Гн, С = 100 мкФ.
Решение
1. Для построения операторной схемы определяем
независимые начальные условия: i3(0+)
= i3(0-) =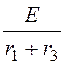
=
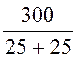= 6 A,
uC(0+) = uC(0-) = r3·i3(0-) = 25·6 = 150 В.
2. Эквивалентная операторная схема показана на рис. 7.83,б.
3. Выполним расчёт схемы методом двух узлов.
u23(p) = uC(p) =
=
=
=
;
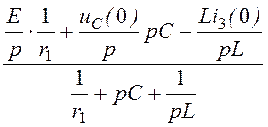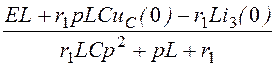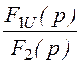I3(p) =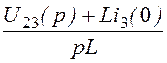
=
=
.
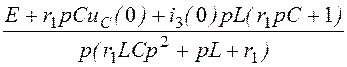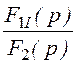4. Оригиналы величин найдём по теореме разложения.
Положим F2(p) = r1LCp2 + pL+ r1 = 5·10 -5p2 + 0,02p+ 25 = 0, корни уравнения р1,2 = -200 ± j678 c -1 = -706,9·e -j73,56°;
F2(0) = 25; F2¢(p) = 10 -4p + 0,02; F2¢(p1) = j0,0678.
Формула для напряжения на конденсаторе: uС(t) = 2Re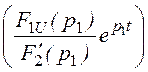
;
F1U(p1) = 300·0,02 + 25·(-200 + j678)·0,02·10 -4·150 – 25·0,02·6 = 5,3·e j73,56°;
uС(t) = 2Re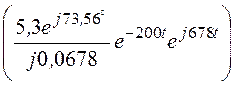
= 156,3e -200tcos(678t
– 16,44°) =
= 156,3e -200tsin(678t + 73,56°)B.
Рассчитываем ток i3(t) =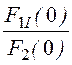
+ 2Re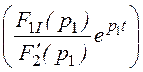
;
F1i(0) = 300; F1i(p1) = 300 + 25·(-200 + j678)·10 -4·150 +
+ 6·(-200 + j678)·0,02·(25·(-200 + j678)·10 -4 + 1) = 265·e j73,56°;
i3(t) =
+ 2Re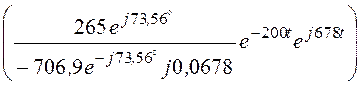
=
= 12 + 11,06e -200tsin(678t – 32,88°)А.
 |
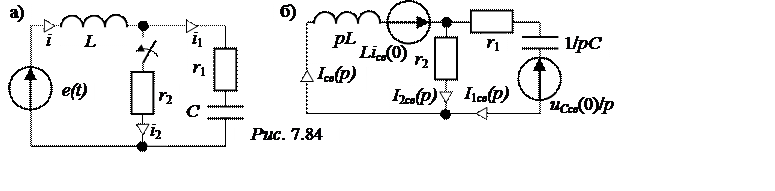L= 0,25 Гн, С = 400 мкФ, r1 = 25 Ом, r2 = 75 Ом.
Решение
1. Рассчитаем независимые начальные условия.
Im =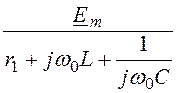
=
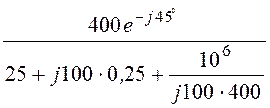= 16·e –j45° А;
UCm = Im·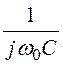
= 16·e –j45°·(-j25) = 400·e –j135° B;
i(t-) = 16sin(w0t – 45°)А; uC(t-) = 400sin(w0t – 135°) B;
i(0+)
= i(0-) = 16sin(-45°) = -8
A,
uC(0+) = uC(0-)
= 400sin(-135°)= -200В.
2. Рассчитаем принуждённые составляющие iпр(t), i2пр(t) и uCпр(t) символическим методом.
Imпр =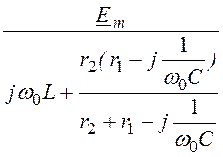
=
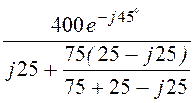= 16·e –j73,05° А;
I2mпр = Imпр·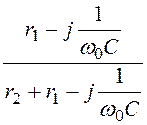
= 16·e –j73,05°·
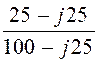= 5,49·e –j104° А;
UCmпр = I1mпр·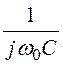= Imпр·
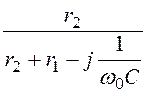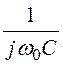·= 16·e –j73,05°·
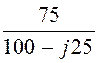·(-j25) =
= 291,4·e –j149,05° В;
i2пр(t) = 5,49sin(w0t – 104°) A, iпр(t) = 16sin(w0t – 73,05°) A,
uCпр(t) = 291,4sin(w0t – 149,05°)В.
Начальные значения принуждённых составляющих:
iпр(0+) = 16sin(-73,05°) = -15,3 A, uCпр(0+) = 291,4sin(-149,05°) = -150 В.
3. Применим операторный метод для определения свободной составляющей тока i2св(t). Для этого определим начальные значения свободных составляющих тока в индуктивности и напряжения на ёмкости:
iсв(0+) = i(0+)
– iпр(0+) = -8+ 15,3 = 4 A,
uCсв(0+)
= uC(0+) – uCпр(0+)
= -200+ 150 = -133 В.
Операторная схема для свободных составляющих представлена на рис. 7.84,б.
4. Полученную схему рассчитаем методом двух узлов.
u12св(p) =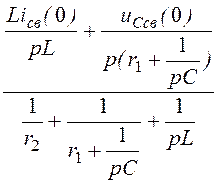
=
;
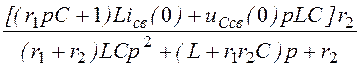I2св(p)
=
=
=
.
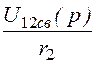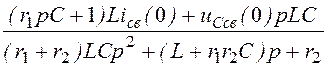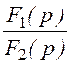Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.