Операторный метод расчёта ПП. Основные теоретические положения, страница 14

С помощью системы MathCAD выполняем вычисление интеграла обратного преобразования Фурье:     u2(t) :=·.

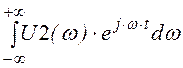Вместо бесконечных пределов возьмём достаточно большие конечные, например, 60000:      u2(t) :=·.

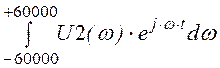Для любого значения времени можно получить ответ. Например,

u2(0.005) = 7.283        u2(0.01) = 19.566             u2(0.05) = 1.361.

Сравните полученные ответы с графиком рис. 7.117,б.

ЗАДАЧА 7.82. Рассчитать напряжение u₂(t) переходного процесса при подключении цепи задачи 5.43 /1/ к источнику постоянного тока    J= 0,05 Aоператорным методом. Формула для комплексного передаточного сопротивления, полученная при решении задачи 5.43:

Z(jw) =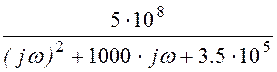 Ом.

Решение

Последовательность решения задачи такая же, как и задачи 7.79. Поэтому приведём лишь ответы.

Операторное передаточное сопротивление Z(р) получаем из комплексного передаточного сопротивления заменой  jw  на  р:

Z(р) := .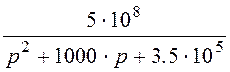

Изображения тока источника и выходного напряжения:

J(s) := J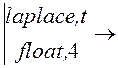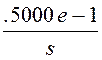,  то есть  J(р) =;  

u2(р) := Z(р)·J(р)      u2(р).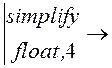

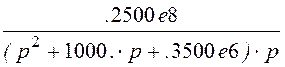Оригинал искомого напряжения получаем с помощью обратного преобразования Лапласа:

u2(t) := u2(р)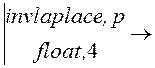 71.43 – 71.43·е ^(-500.)·t·cos(316.2·t) –

 – 112.9·е ^(-500.)·t·sin(316.2·t).

ЗАДАЧА 7.83. Решить задачу 7.82 с помощью интеграла Дюамеля, операторным и спектральным методом при условии, что источник вырабатывает одиночный импульс тока, график которого приведен на рис. 7.117,а. Построить график вы-ходного напряжения.

Решение

Последовательность решения задачи такая же, как и задачи 7.81. Поэтому приведём лишь ответы.

1.Z(р) := .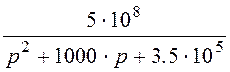

Переходная характеристика

g(t) := Z(р)·

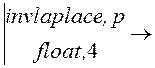
® 1429. – 1429.·е ^(-500.)·t·cos(316.2·t) – 2259.·е ^(-500.)·t·sin(316.2·t).

Импульс входного тока аналитически описывается двумя формулами:

- на интервале  0 £t£ t₁ = 0,01 с     j1(t) := 0.01 + 4·t;

- на интервале  t₁£ t                         j2(t) := 0.

Искомое напряжение при   0 £ t £ t₁ = 0,01 с:

u21(t) := j1(0)·g(t) +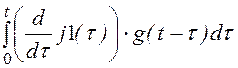

u21(t) 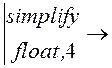 (-2.040) + 5716.·t + 2.040·e ^(-500.)·t·cos(316.2·t) –

– 14.85·e ^(-500.)·t·sin(316.2·t).

При   t ³ t₁

u22(t) := j1(0)·g(t) +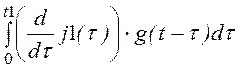+ (0 – j1(t1))·g(t – t1)

u22(t) 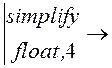 2.040·e ^(-500.)·t·cos(316.2·t) – 14.85·e ^(-500.)·t·sin(316.2·t) +

+ 55.12·e ^{(-500.)·t + 5.}·cos(316.2·t – 3.162) + 105.2·e ^{(-500.)·t + 5.}·sin(316.2·t – 3.162).

Ответ записываем в следующем виде:    u2(t) :=  0 if  t < 0

u21(t) if  0 £ t £ t1

u22(t) otherwise

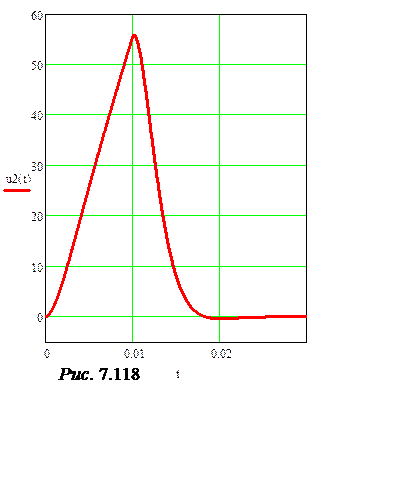
График напряжения построен на рис. 7.118.

2. Выполним расчёт операторным методом. Оригинал тока источника:

j(t) := (0.01 + 4·t)·(Ф(t) – Ф(t – t1)).

Изображение тока источника:

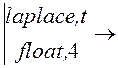
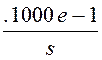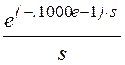J(s) := j(t) – .5000e-1·+– 4.·.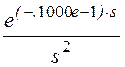

Изображение выходного напряжения:   u2(р) := Z(р)·J(р).

u2(р)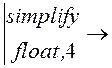(-.5е7)·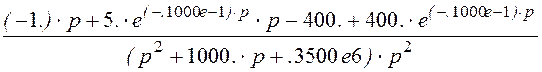

Оригинал выходного напряжения:

u2(t) :=u2(р) 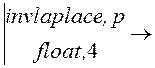 (-2.041) + 2.041·e ^(-500.)·t·cos(316.2·t) –

– 14.84·e ^(-500.)·t·sin(316.2·t) + 2.041·Ф(t – .1000е-1) +

+ 55.10·Ф(t – .1000е-1)·e ^{(-500.)·t + 5.}·cos(316.2·t – 3.162) +

+ 105.2·Ф(t – .1000е-1)·e ^{(-500.)·t + 5.}·sin(316.2·t – 3.162) +

+ 5714.·t – 5714.·t·Ф(t – .1000е-1).

График напряжения, построенный по последней формуле, приведен на рис. 7.118.

3. Выполним расчёт спектральным методом.

Спектральная плотность тока источника, полученная по изображению тока источника,

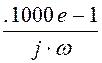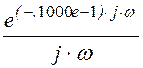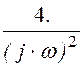J(w) := – .5000e-1·+– 4.·.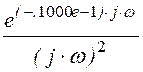

Спектральная плотность выходного напряжения находится через комплексное передаточное сопротивление:u2(w) := Z(w)·J(w), где комплекс-ное передаточное сопротивление

Z(w) = .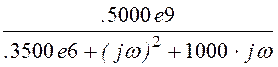

С помощью системы MathCAD выполняем вычисление интеграла обратного преобразования Фурье:     u2(t) :=·.

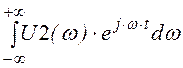Вместо бесконечных пределов возьмём достаточно большие конечные, например, 60000:       u2(t) :=·.

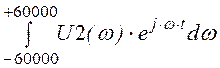Для любого значения времени можно получить ответ. Например,

u2(0.005) = 25.311        u2(0.01) = 55.09             u2(0.015) = 8.595.

Сравните полученные ответы с графиком рис. 7.118.

Подытоживая анализ задач 5.42, 5.43, 6.5, 7.79 – 7.83, можем сказать, что при помощи комплексной передаточной функции можно определить реакцию цепи при любой форме воздействия.