ЗАДАЧА 7.76.
Определить спектральную плотность следующих сигна-лов: а) f(t)
=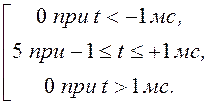 б) f(t) =
б) f(t) =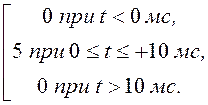
в)f(t)
=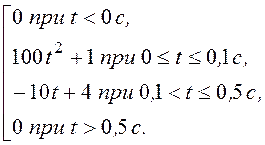
Решение
а). Воспользуемся прямым преобразованием Фурье:
F(jw) =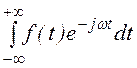 =
=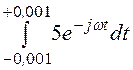 =
=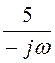 е -jwt
е -jwt![]() =
=
=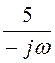 (е-jw·0,001 – е+jw·0,001)
=
(е-jw·0,001 – е+jw·0,001)
=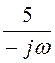 ·(-j2sin(0,001w)) =
·(-j2sin(0,001w)) =![]() sin(0,001w).
sin(0,001w).
б). Так как функция f(t) равна нулю при t < 0, то можно воспользоваться таблицами преобразования Лапласа. Разложим заданный прямоугольный импульс на две ступенчатые составляющие с амплитудами 5 и -5, причём вторая составляющая запаздывает на 10 мс. Их изображения (по Лапласу):
![]() и -
и -![]() е -р·0,01.
е -р·0,01.
Изображение заданного импульса F(р) =![]() –
– ![]() е -р·0,01 =
е -р·0,01 =![]() (1 – е -р·0,01).
(1 – е -р·0,01).
Спектральную плотность получим, если в ответе заменим р на jw:
F(jw) =![]() (1 – е -jw·0,01).
(1 – е -jw·0,01).
в). Воспользуемся преобразованиями Лапласа, но выполним их с помощью системы MathCAD. Исходная функция, записанная одной формулой с помощью функции Хевисайда 1(t) = Ф(t):
f(t) := (100t2 + 1)·(Ф(t) – Ф(t– 0,1)) + (-10t + 4)·(Ф(t– 0,1) – Ф(t– 0,5)).
Изображение функции:
f(t)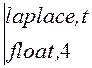 ®
®![]() +
+ 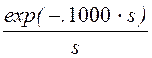 – 30.·
– 30.·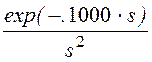 –
–
– 200.·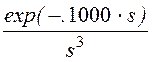 +
+![]() +
+ 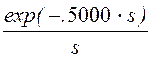 + 10.·
+ 10.·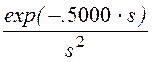
или F(р) =![]() (1 + е -0,1р +
е -0,5р) +
(1 + е -0,1р +
е -0,5р) +![]() (-3е -0,1р +
е -0,5р) +
(-3е -0,1р +
е -0,5р) +![]() (1 – е -0,1р).
(1 – е -0,1р).
Искомая спектральная плотность
F(jw) =![]() (1 + е -0,1jw + е -0,5jw) +
(1 + е -0,1jw + е -0,5jw) +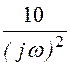 (-3е -0,1jw + е -0,5jw) +
(-3е -0,1jw + е -0,5jw) +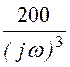 (1 – е -0,1jw).
(1 – е -0,1jw).
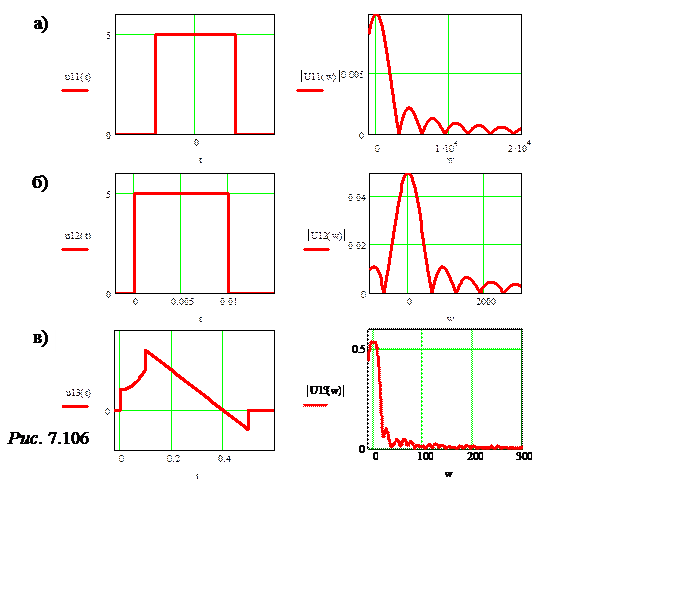
Графики функций и их спектры представлены на рис. 7.106.
 |
ЗАДАЧА 7.77.
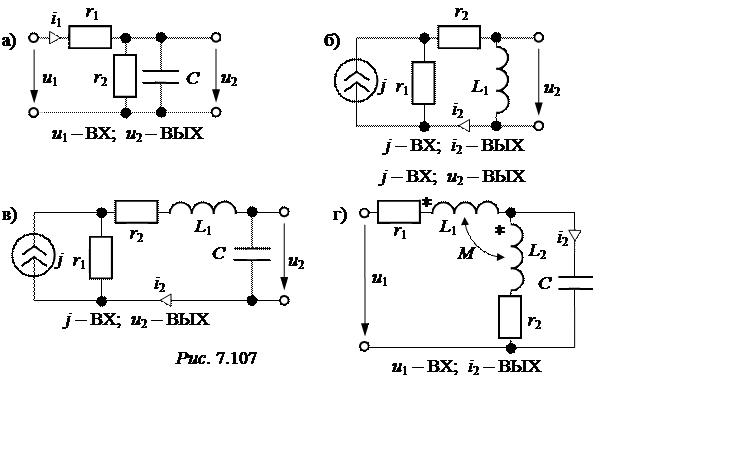
Определить комплексную передаточную функцию, построить её АЧХ и ФЧХ для цепей
рис. 7.107 при следующих числовых значениях: r1 = 100 Ом, r2 = 200 Ом, С = 10 мкФ, L1= 0,1 Гн, L2= 0,02
Гн, М = 0,9![]() = 0,04 Гн. Под каждым
рисунком указано, какая величина счи-
= 0,04 Гн. Под каждым
рисунком указано, какая величина счи-
 |
Решение
а). Примем u2 = 1. Тогда i1 = u2(r2-1+ jwС) =r2-1+ jwС;
u1 = u2 + r1i1 = 1 + r1(r2-1+ jwС).
КПФ по напряжению
Н1(jw) = u2/u1 =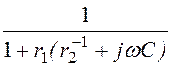 =
=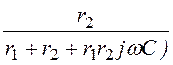 =
=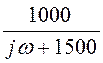 .
.
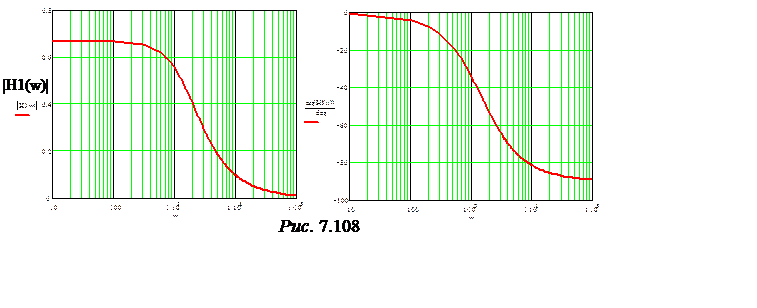 Графики АЧХ Н1(w) =|Н1(jw)| и ФЧХ Y1(w) = arg(Н1(jw)) представлены на рис. 7.108.
Графики АЧХ Н1(w) =|Н1(jw)| и ФЧХ Y1(w) = arg(Н1(jw)) представлены на рис. 7.108.
б). По правилу разброса тока в параллельные ветви i2 = j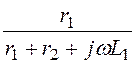 .
.
КПФ по току Нi(jw) = i2/j =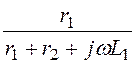 =
=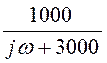 .
.
Графики АЧХ и ФЧХ функции Нi(jw) аналогичны графикам рис. 7.109.
Если в качестве выходной величины выступает напряжение u2, то комплексное передаточное сопротивление
Н2(jw)
= u2/j
= jwL1i2/ j
=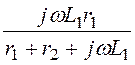 =
=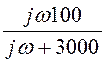 Ом.
Ом.
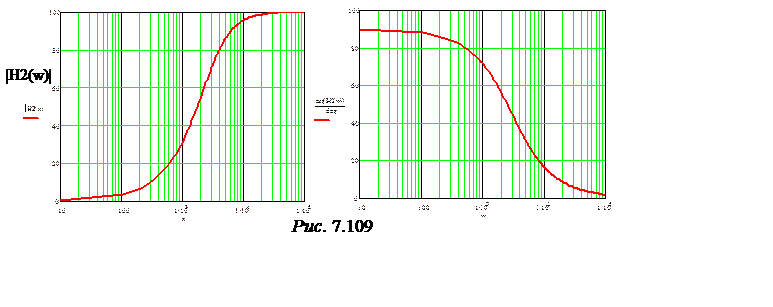 Графики АЧХ и ФЧХ функции Н2(jw) представлены на рис. 7.109.
Графики АЧХ и ФЧХ функции Н2(jw) представлены на рис. 7.109.
в). В этой схеме
i2 = j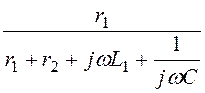 и u2 =
и u2 =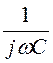 ·i2 = j
·i2 = j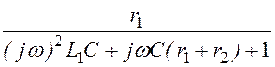 .
.
Комплексное передаточное сопротивление
Н3(jw) = u2/j =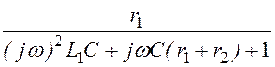 =
=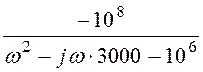 Ом.
Ом.
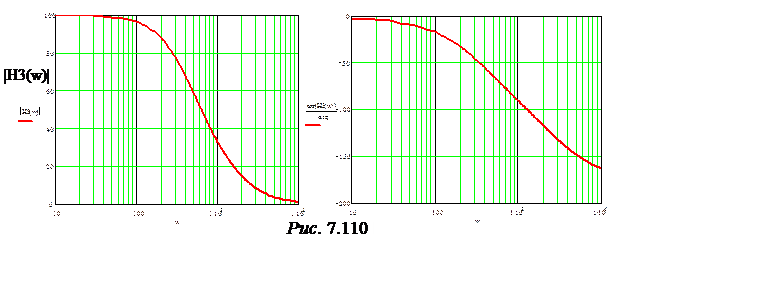 Графики АЧХ и ФЧХ представлены на рис. 7.110.
Графики АЧХ и ФЧХ представлены на рис. 7.110.
г). Запишем систему уравнений относительно контурных токов i1 и i2:
(r1+ r2+ jwL1+ jwL2 + j2wM)i1– (r2+ jwL2 + jwM)i2 = U1,
![]() -(r2+ jwL2 + jwM)i1 + (r2 + jwL2 +
-(r2+ jwL2 + jwM)i1 + (r2 + jwL2 +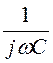 )i2=
0.
)i2=
0.
Найдём способом подстановки:
i1 = i2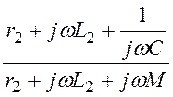 ,
,
i2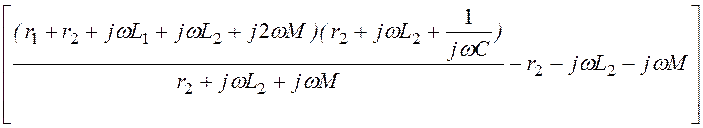 = U1.
= U1.
Комплексная передаточная проводимость
Н4(jw) =![]() =
=
=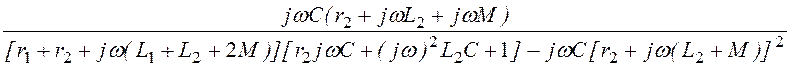 =
=
=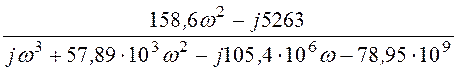 Cм.
Cм.
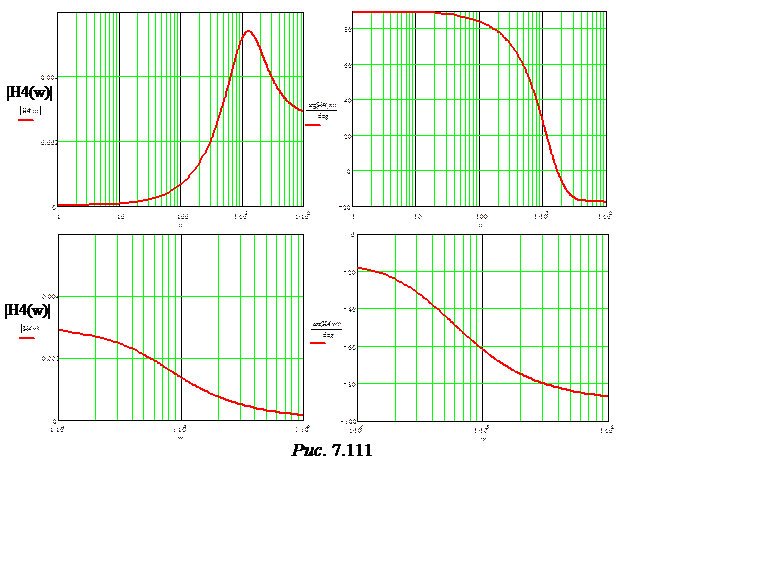 Графики АЧХ и ФЧХ представлены на рис. 7.111.
Графики АЧХ и ФЧХ представлены на рис. 7.111.
ЗАДАЧА 7.78. Для указанных ниже цепи (берётся из задачи 7.76) и воздействия (из задачи 7.77) получить спектр и функцию времени выходной величины: 1) цепь а), воздействие а); 2) цепь б), воздействие б); 3) цепь в), воздействие б); 4) цепь в), воздействие в).
Решение
1. Цепь а) обеспечивает КПФ Н1(w) :=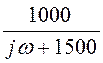 , воздействие а) пред-ставлено спектром U1(w) :=
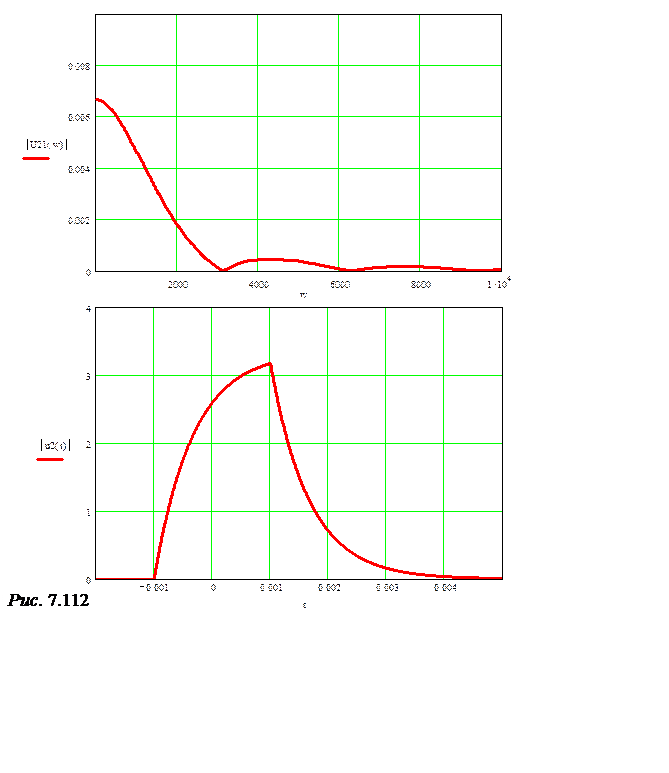
, воздействие а) пред-ставлено спектром U1(w) :=![]() sin(0,001w) В·c. Тогда спектральная плотность выходного напряжения U2(w) := Н1(w)·U1(w), U2(w) =
sin(0,001w) В·c. Тогда спектральная плотность выходного напряжения U2(w) := Н1(w)·U1(w), U2(w) =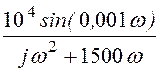 В·c.
В·c.
Оригинал напряжения (функция времени):
u2(t) := U2(w)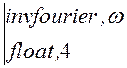 ® -3.334·ехр(-1500.·t – 1.500)·Ф(1.·t + 1.000·10-3)
…
® -3.334·ехр(-1500.·t – 1.500)·Ф(1.·t + 1.000·10-3)
…
 |
2. Цепь б) обеспечивает КПФ Н2(w) :=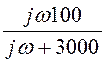 Ом, воздействие б) представлено спектром j(w) :=
Ом, воздействие б) представлено спектром j(w) :=![]() (1 – е –jw·0,01) А·c.
Тогда спектральная плот-ность выходного напряжения
(1 – е –jw·0,01) А·c.
Тогда спектральная плот-ность выходного напряжения
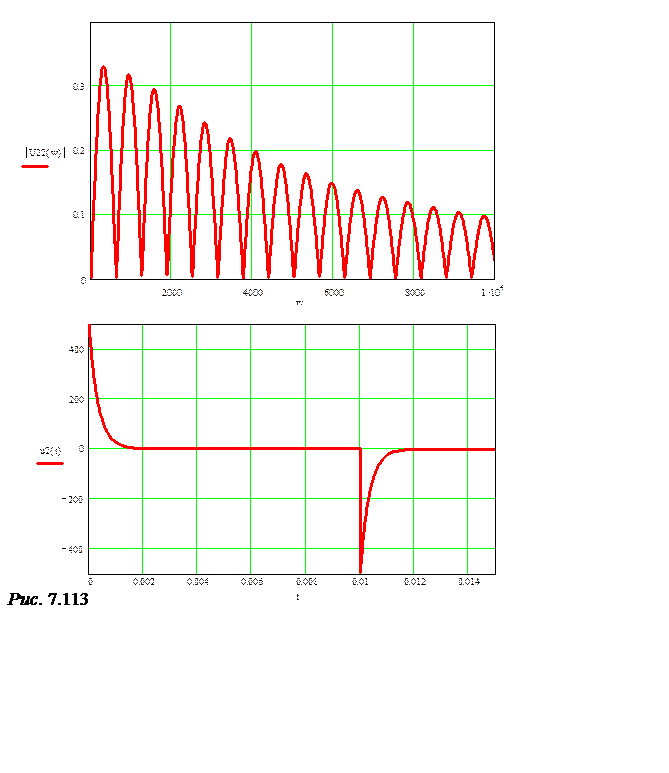
U2(w) := Н2(w)·j(w), U2(w) =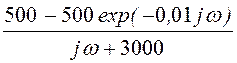 В·c.
В·c.
Оригинал напряжения (функция времени):
u2(t) := U2(w)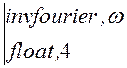 ® 500.2·ехр(-3000.·t)·Ф(1.·t) – 500.2·ехр(-3000.·t + …
® 500.2·ехр(-3000.·t)·Ф(1.·t) – 500.2·ехр(-3000.·t + …
 |
3. Цепь в) обеспечивает КПФ Н3(w) :=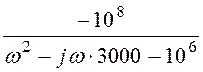 Ом, воздей-ствие б) представлено спектром j(w) :=
Ом, воздей-ствие б) представлено спектром j(w) := ![]() (1 – е –jw·0,01) А·c.
Тогда спектраль-ная плотность выходного напряжения
(1 – е –jw·0,01) А·c.
Тогда спектраль-ная плотность выходного напряжения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.