ЗАДАЧА 7.55. Решить задачу 7.18 операторным методом.
Решение
Задачу решим, используя в качестве вычислительной техники MathCAD. Отметим, что в MathCAD в качестве операторной переменной р используется переменная s; единичная скачкообразная функция 1(t) Хевисайда обозначается Ф(t).
Исходные данные: t:= 0.6·10 -3 r1 := 20 r2 := 30 С := 5·10 -5.
ЭДС источника в виде прямоугольного импульса, записанная с помощью функции Хевисайда: Е(t) := 100·(Ф(t) – Ф(t– t)).
Изображение ЭДС: Е(t)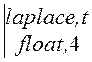 ®
® ![]() –
100·
–
100·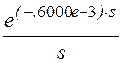 .
.
Перезадаём ЭДС: ЕЕ(s) :=![]() – 100·
– 100·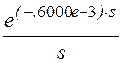 .
.
Входное операторное сопротивление цепи:
Z(s) := r1 +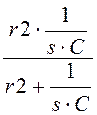 Z(s)
Z(s) 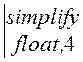 ® 20.·
® 20.·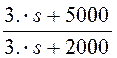 .
.
Изображения токов:
i1(s) :=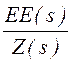 i2(s) := i1(s)·
i2(s) := i1(s)·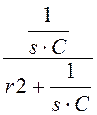 i3(s) := i1(s)·
i3(s) := i1(s)·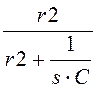 .
.
Оригиналы токов:
i1(s)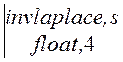 ®2.+3.·е (-1667.)·t – 2.·Ф(t –.6000е-3) – 3.·Ф(t
–.6000е-3)·е (-1667.)·t+1
®2.+3.·е (-1667.)·t – 2.·Ф(t –.6000е-3) – 3.·Ф(t
–.6000е-3)·е (-1667.)·t+1
i2(s)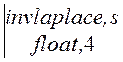 ®2.–2.·е (-1667.)·t – 2.·Ф(t –.6000е-3) + 2.·Ф(t
–.6000е-3)·е (-1667.)·t+1
®2.–2.·е (-1667.)·t – 2.·Ф(t –.6000е-3) + 2.·Ф(t
–.6000е-3)·е (-1667.)·t+1
i3(s)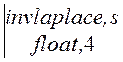 ® 5.·е (-1667.)·t – 5.·Ф(t–.6000е-3)·е
(-1667.)·t+1.
® 5.·е (-1667.)·t – 5.·Ф(t–.6000е-3)·е
(-1667.)·t+1.
Для построения графиков токов их нужно перезадать:
i1(t) := 2.+3.·е (-1667.)·t – 2.·Ф(t –.6000е-3) – 3.·Ф(t –.6000е-3)·е (-1667.)·t+1
i2(t) := 2.–2.·е (-1667.)·t – 2.·Ф(t –.6000е-3) + 2.·Ф(t –.6000е-3)·е (-1667.)·t+1
i3(t) = 5.·е (-1667.)·t – 5.·Ф(t–.6000е-3)·е (-1667.)·t+1.
 Полученные ответы для токов при необходимости путём
некоторых преобразований могут быть приведены к виду ответов к задаче 7.18.
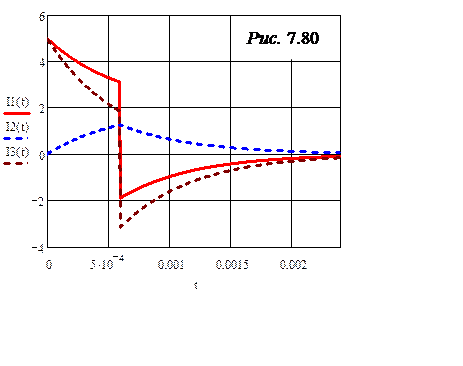
Графики токов приведены на рис. 7.80.
Полученные ответы для токов при необходимости путём
некоторых преобразований могут быть приведены к виду ответов к задаче 7.18.
Графики токов приведены на рис. 7.80.
ЗАДАЧА 7.56. Решить за-дачу 7.19 операторным методом.
Решение
 Примем, что прямоуголь-ные импульсы начинают посту-пать
с момента времени t = 0. Это допущение необходимо в связи с тем, что
преобразования Лапласа осуществляются только для t
³ 0. Период источника составляет, согласно условию, 2t. Поскольку учёт действия бесконечно большого числа импульсов источника
вызывает затрудне-ния (см. задачу 7.57), рассмотрим их ограничен-ное
количество. Так как практическая длитель-ность переходного процесса составляет
5t, то есть менее трёх периодов, достаточно учесть три
периода (импульса) до начала расчётного (рабочего) периода, находящегося в
диапазоне 3Т £ t£ 4Т.
Примем, что прямоуголь-ные импульсы начинают посту-пать
с момента времени t = 0. Это допущение необходимо в связи с тем, что
преобразования Лапласа осуществляются только для t
³ 0. Период источника составляет, согласно условию, 2t. Поскольку учёт действия бесконечно большого числа импульсов источника
вызывает затрудне-ния (см. задачу 7.57), рассмотрим их ограничен-ное
количество. Так как практическая длитель-ность переходного процесса составляет
5t, то есть менее трёх периодов, достаточно учесть три
периода (импульса) до начала расчётного (рабочего) периода, находящегося в
диапазоне 3Т £ t£ 4Т.
С учётом сказанного, ЭДС источника записывается формулой:
Е(t) := 100·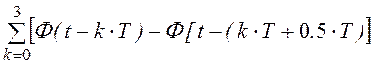 .
.
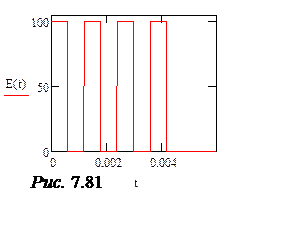
Для контроля выведем график Е(t) (рис. 7.81).
Изображение ЭДС представляется довольно длинной формулой, поэтому приводим её в уменьшенном виде:
![]()
Перезадаём ЭДС:
![]()
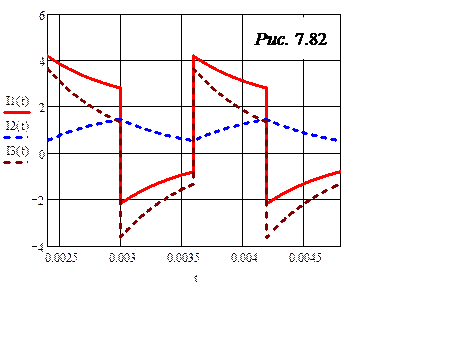
Поскольку цепь та же, что и в задаче 7.55, формулы для входного сопротивления, изображений и оригиналов будут теми же, что и в задаче 7.55. Ответы для токов, по которым построены графики рис. 7.82, выглядят следующим образом:
i1(t) :=2.+3.·е (-1667.)·t –2.·Ф(t–.6000е-3)–3.·Ф(t –.6000е-3)·е (-1667.)·t+1+
+2.·Ф(t–.1200е-2)+3.·Ф(t–.1200е-2)·е (-1667.)·t+2–2.·Ф(t–.1800е-2)–…
i2(t) :=2.–2.·е (-1667.)·t –2.·Ф(t–.6000е-3) + 2.·Ф(t–.6000е-3)·е (-1667.)·t+1+ …
i3(t) = 5.·е (-1667.)·t –5.·Ф(t–.6000е-3)·е (-1667.)·t+1+5.·Ф(t–.1200е-2)·е (-1667.)·t+2 …
 У первого и второго токов в ответе содержится 16
слагаемых, у третьего – 8.
У первого и второго токов в ответе содержится 16
слагаемых, у третьего – 8.
На графиках рис. 7.82 рабочим участком является диапазон 0,0036 с £ t£ 0,0048 с.
ЗАДАЧА 7.57. Задачу 7.22 решить операторным методом, используя способ расчёта установившейся реакции путём суммирования изображений реакций в области комплексного переменного.
Решение
Рассчитаем изображение по Лапласу первого импульса напряжения на интервале 0 £ t £ t0
U1(p) =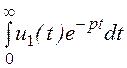 =
=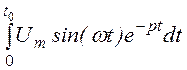 =
=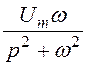 (1
+
(1
+ ![]() ).
).
Для определения изображения напряжения просуммируем n одинаковых импульсов, смещённых во времени на период T. Получим
U(p) = U1(p)[1 + e -pT + e -2pT + … +e –(n-1)pT].
Для установившегося режима n ® ¥
U(p) = U1(p)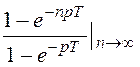 = U1(p)
= U1(p)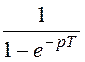 =
=
=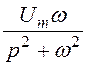 (1+
(1+![]() )
)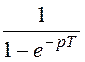 =
=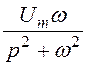
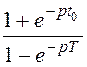 .
.
Изображение тока на n-м интервале при n ® ¥
I(p) =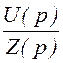 =
=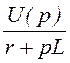 =
=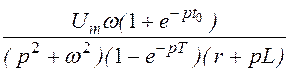 =
=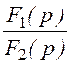 .
.
Полюс изображения,
полученный из уравнения Z(p) = r + pL = 0, p1= -r/L = -t -1 = -25 c -1, определяет свободную
составляющую тока, которая рассчитывается по теореме разложения iсв(t)
=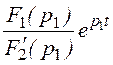 , где F2¢(p1) = (p12+ w2)(1
–
, где F2¢(p1) = (p12+ w2)(1
– ![]() )L.
)L.
Тогда
iсв =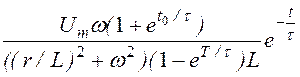 = Imsinj
= Imsinj 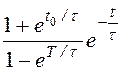 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.