U2(w) := Н3(w)·j(w), U2(w) =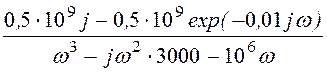 В·c.
В·c.
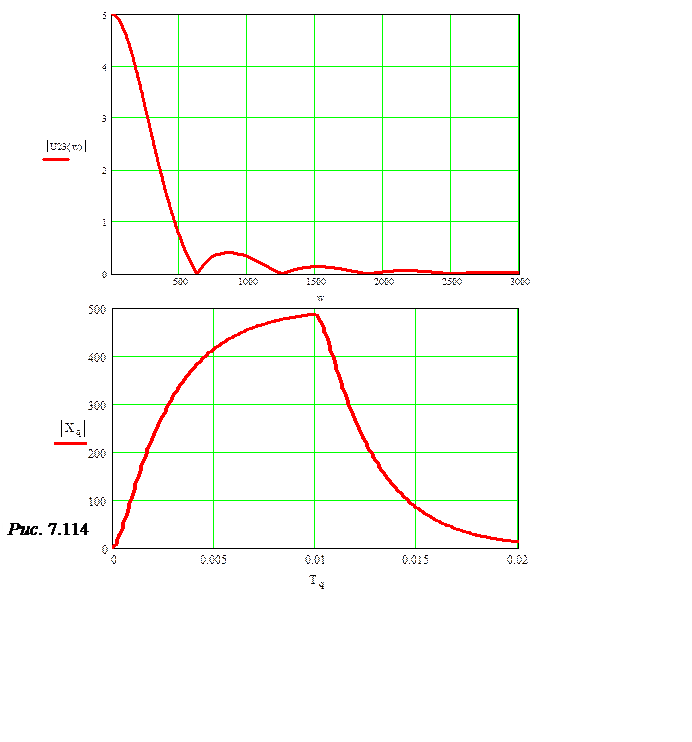
Спектр напряжения см. на рис. 7.114.
Оригинал напряжения (функция времени) с помощью функции invfourier не удаётся получить. Поступим другим образом. Применим формулу обратного преобразования Фурье, в которой вместо теоретических бесконечных пределов возьмём достаточно большие числа ±60000:
 |
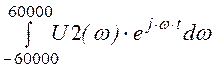 .
.
Однако по этой формуле MathCAD не строит график (программа зависает). Сформируем массив из 201 значения функции с временным шагом 0,0001:
dt := 0.0001 q := 0 .. 200 Tq := q·dt Xq := u2(Tq)
График зависимости Xq(Tq) представлен на рис. 7.114.
4. Цепь в) обеспечивает КПФ Н3(w) :=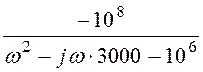 Ом, воздей-ствие в) представлено спектром
Ом, воздей-ствие в) представлено спектром
j(w) := ![]() (1 + е -0,1jw + е -0,5jw) +
(1 + е -0,1jw + е -0,5jw) +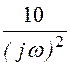 (-3е -0,1jw + е -0,5jw) +
(-3е -0,1jw + е -0,5jw) +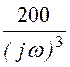 (1 – е -0,1jw) А·c.
(1 – е -0,1jw) А·c.
Тогда спектральная плотность выходного напряжения
U2(w) := Н3(w)·j(w).
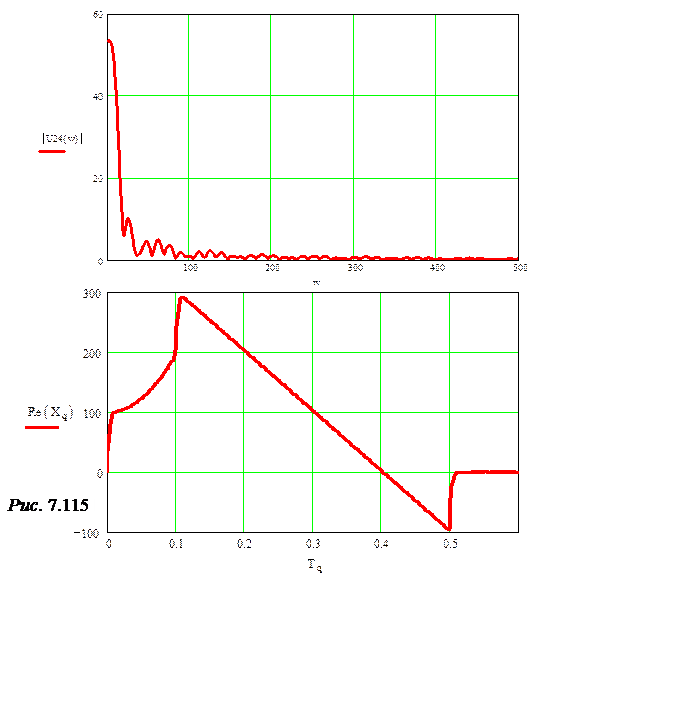
Спектр напряжения см. на рис. 7.115.
 |
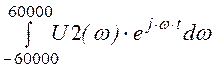 .
.
Сформируем массив из 401 значения функции с временным шагом 0,0015: dt := 0.0015 q := 0 .. 400 Tq:= q·dt Xq:= u2(Tq)
График зависимости Xq(Tq) представлен на рис. 7.115
Вывод. Спектральный метод является перспективным, позволяет автоматизировать анализ переходных процессов в цепях. Однако его использование предполагает наличие достаточно мощной вычислительной техники. Система MathCAD поддерживает этот метод лишь при решении сравнительно простых задач (цепи не более второго порядка, воздействия, описываемые одной-двумя формулами).
7.5. иСПОЛЬЗОВАНИЕ КОМПЛЕКСНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ (кпф) ПРИ РАСЧЁТЕ пп
ЗАДАЧА 7.79.
Рассчитать напряжение u2(t) (выходная величина) переходного процесса при
подключении цепи задачи 5.42 /1/ к источнику постоянного тока (входная
величина) J=
0,05 A классическим
и операторным методами. Формула для комплексного передаточного сопротивления,
полу-ченная при решении задачи 5.42: Z(jw) =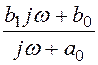 =
=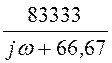 Ом.
Ом.
Решение
1. При решении задачи классическим методом напряжение u2(t) ищется в виде суммы принуждённой и свободной составляющих:
u2(t) = u2пр(t) + u2св(t).
Поскольку источник постоянный, принуждённая составляющая также является постоянной и может быть определена через комплексное передаточ-ное сопротивление при частоте w = 0:
Z(0) =![]() =
=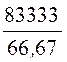 = 1250 Ом; u2пр = Z(0)·J = 1250·0,05 = 62,5 В.
= 1250 Ом; u2пр = Z(0)·J = 1250·0,05 = 62,5 В.
Комплексное передаточное сопротивление является так называемой системной функцией. Для получения характеристического уравнения нужно в ней заменить jw на р и знаменатель дроби приравнять к нулю. Получаем:
р + а0 = 0, р = -а0 = -66,67 с -1.
При одном корне характеристического уравнения свободная составляющая имеет вид: u2св(t) = А·е рt, где постоянная интегрирования А находится из начальных условий – А = u2св(0) = u2(0) – u2пр(0).
Для получения начального
значения напряжения u2(0)
снова используем комплексное передаточное сопротивление, но теперь при частоте,
равной бесконечности: Z(¥) =![]() =
=![]() = 0.
= 0.
Тогда u2(0) = Z(¥)·J = 0, и А = -u2пр(0) = -62,5.
Окончательно получаем:u2(t) = 62,5 – 62,5·е -66,67t В.
2. Для расчёта выходного напряжения u2(t) операторным методом используем операторное передаточное сопротивление Z(р), которое получаем из комплексного передаточного сопротивления заменой jw на р:
Z(р) =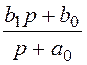 =
=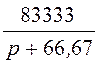 .
.
Изображения тока источника и выходного напряжения (используем MathCAD):
J(s) := J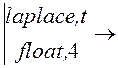
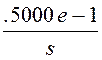 , то есть J(р)
=
, то есть J(р)
=![]() ;
;
u2(р) := Z(р)·J(р) u2(р)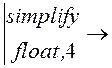
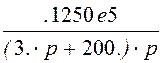 .
.
Оригинал искомого напряжения получаем с помощью обратного преобразования Лапласа:
u2(t) :=u2(р)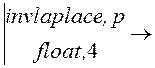 62.5 – 62.5·е
(-66,67)·t.
62.5 – 62.5·е
(-66,67)·t.
ЗАДАЧА 7.80. Решить задачу 7.79 спектральным методом при условии, что источник вырабатывает одиночный прямоугольный импульс тока амплитудой J= 0,05 Aи длительностью t= а0 -1 = 0,015 с.
Решение
Мгновенное значение тока
воздействия может быть записано аналитически следующим образом: J(t) : =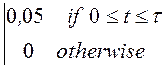 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.