В большой части работы в рамках Национальной Программы Многоцикловой Усталости Турбинных Механизмов[23, 24], процедура пошаговой нагрузки использовалась, чтобы получить данные FLS. Использовались типичные шаги 107 циклов, в то время как __ как правило бралось в 5 % начального блока нагрузки. Пошаговая процедура нагрузки показана схематично на рисунке 3.2 для блоков 107 циклов. Размер шага зависит от степени точности, желаемой при определении FLS. Такие высокие шаги как 20 % первоначального блока напряжения использовались, чтобы оценить эффекты FOD на пределе усталости [25]. В случаях, при которых степень повреждения из-за FOD является очень переменной, точное определение FLS не гарантировано. Вдобавок, стартовое напряжение для первого блока не очень предсказуемо, таким образом, маленькие приращения могли привести к очень большому числу шагов и, следовательно, долгому времени проверки.
Есть некоторые преимущества для использования предложенной техники, кроме значительных сбережений в тестировании времени. Предложенная техника приводит к отказу в каждом экземпляре, вопреки обычному тестированию усталости, где некоторое количество проверенных экземпляров проваливают тест, а другие продолжают, не потому что тест закончен после большого количества циклов (выход).
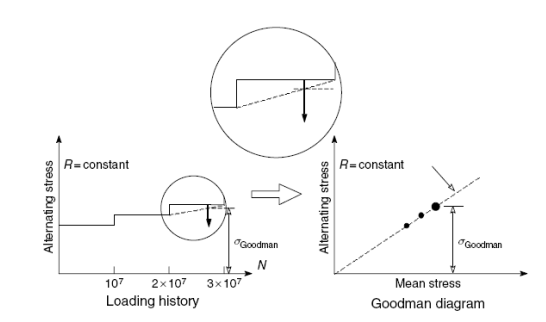
Рисунок 3.2 Схематичное изображение процедуры пошаговой нагрузки
Это приводит к двум разновидностям экземпляров, одни неудачные и другие удавшиеся, которые трудно проанализировать статистически. Другой аргумент за использование непостоянной нагрузки для определения предела усталости это то, что, как указывает Прот[14], “практически, усталостные нагрузки не являются регулярно переменными, но они являются неоднородными по амплитуде нагрузки.”
Одна из главных проблем в установлении материала, допустимого для МЦУ является редко доступный объем данных и время, необходимое, чтобы установить частные значения для пределов усталости при 107 циклах или больше. Обычный метод для того, чтобы определить предел усталости, необходимо получить данные S–N по диапазону усилий и представить данные некоторым типом кривой или прямолинейной аппроксимации. Для предела усталости в 107 циклов, например, это требует числа тестов усталости, некоторые из которых будут сверх 107 циклов. Это и занимает долгое время и является дорогостоящим. Единственный метод для того, чтобы уменьшить время, это использовать высокочастотную испытательную машину, такую как одна из тех, которые появились на рынке в течение прошлых нескольких лет. Кроме того, использование быстрой испытательной техники, также как и однажды развитое Максвеллом и Николасом [22] использование пошаговой нагрузки, описанное выше, может сэкономить значительное время тестирования. Было продемонстрировано, что такая техника обеспечивает данные для предела усталости сплава титана, которые совместимы с полученными в обычной методе S–N [22, 26].
3.3.1 Статистические соображения
Чтобы исследовать ожидаемый результат использования техники пошаговой нагрузки, рассмотрим схему на рисунке 3.3. Можно определить предел усталости на кривой S–N произвольно как Nf, даже хотя нет никакой гарантии, что это - истинный усталостный предел, соответствующий "бесконечной" жизни. При Nf будет существовать неизвестная функция совокупного распределения (CDF), которая определит функцию отказа при числе циклов свыше некоторого диапазона напряжений.
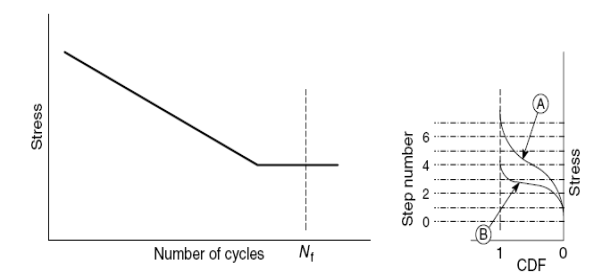
Рисунок 3.3 Схематичное изображение кривой S-N и CDF для двух различный степеней разброса
Напряжение, соответствующее CDF =0, определяет уровень напряжения, ниже которого нет никаких отказов в пределах циклов Nf. Когда CDF = 1, соответствующее напряжение определяет условие, при котором все экземпляры терпят неудачу при или ниже циклов Nf (*). Если будет большое количество разброса, как в кривой "A", который может произойти, если кривая S–N будет очень плоской, то большее число шагов в методе пошаговой нагрузки будет обязано охватывать все возможные значения напряжения, при которых отказ может произойти ниже количества цикла, которое рассматривают, а именно Nf. Если, однако, есть меньше разброса как в кривой “B”, или кривая S–N более крута, что, по существу, отключит более высокие значения напряжения, которые вызывают отказ при более низких числах циклов, то число шагов - меньше. В любом случае, чем больше число шагов в тесте, тем выше ожидаемое напряжение. Таким образом, что, как могло бы казаться, является эффектом "коаксинга", не более, чем статистика распределения силы усталости материала. Фактическое число шагов в эксперименте пошаговой нагрузки зависит от стартового напряжения, функции распределения или диапазона в уровнях напряжения, и размера шага.
Альтернативой подходу пошаговой нагрузки для того, чтобы определить предел усталости, является необходимость проведения тестов при различных значениях напряжения до числа циклов, соответствующих пределу усталости. Получены два типа данных. Во-первых, некоторые экземпляры потерпят неудачу прежде, чем Nf достигнут, и они обеспечат данные для кривой S–N, которая может быть использована и приближена к Nf. Второй тип данных будет уровнями напряжения, для которых никакой отказ не был получен в пределах циклов Nf. Эти уровни напряжения будут обозначены как выходы или более низкие границы на пределе усталости. В проведении тестов при постоянным напряжении рассмотрим случай, когда кривая S–N является относительно плоской, такой же, когда число циклов, Nf, является очень большим. Как гипотетический пример, рассмотрим поведение усталости в диапазоне между 107 и 109 циклами, где, как это было показано, у кривой S–N все еще есть немного отрицательный наклон для некоторых материалов [27].
* Здесь нужно отметить, что некоторые математические представления функций распределения могут идти от ноля до бесконечности, такие как нормальное распределение. В тех случаях мы должны иметь дело с ситуацией, когда CDF приближается к 0 или к 1 в пределах некоторой очень маленькой вероятности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.