где w - экспонента Волкера. За исключением значения коэффициента в Уравнении (2.13), оно идентично по форме уравнению SWT при w = 0.5. Иллюстрация 2.29 изображает уравнения Волкера при различных значениях экспоненты w, включая расширение уравнения, чтобы включить отрицательное среднее напряжение, или значения R <−1. Все кривые вынуждены пройти точку при нулевом среднем напряжении. В то время как некоторые данные обработаны, изменяя значения w для отрицательных значений R, можно заметить, что у уравнения Волкера есть те же самые общие особенности, как и у уравнения SWT для отрицательного среднего напряжения, а именно, переменное напряжение продолжает увеличиваться, поскольку среднее напряжение идет в отрицательную стороне. Далее, для обоих уравнений, форма кривых для положительного среднего напряжения является вогнутой по всей области.
Несколько попыток были сделаны в ранние периоды моделирования усталости, чтобы описать наблюдаемое поведение FLS, когда среднее напряжение было отрицательно. В 1930, Хай [30] указал, что экспериментальные данные указывают на то, что диаграмма постоянной жизни не является симметричной относительно _ m, как требует формула Гербера и обобщенная формула Гудмана. ∗
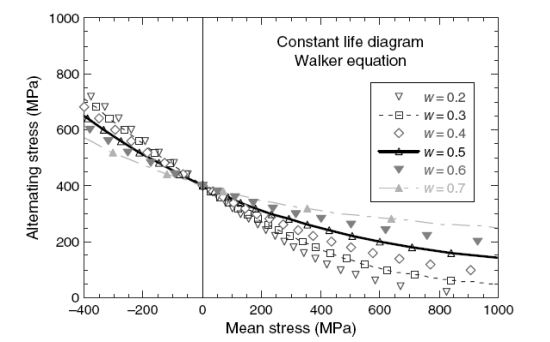
Рисунок 2.29. Диаграмма Хая, представленная уравнением Волкера.
Он предположил, что данные могут быть представлены обобщенным параболическим отношением
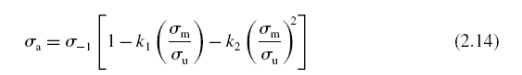
где константы k1 и k2 отобраны, чтобы дать лучшее описание данных. Изображение этого уравнения представлено в иллюстрации 2.30 для нескольких комбинаций k1 и k2, ограничивающих кривые пройти точку предельного напряжения на оси X и значения переменного напряжения при R = − 1 по оси Y. Случай, где k1 = 0 _ k2 = 1 представляет параболу Гербера, Уравнение (2.5), симметрический относительно оси Y. Когда k1 =1 и k2 =0, получается измененная линия Гудмана, экстраполированная для отрицательного среднего напряжения.
Были предложены более сложные уравнения, такие как уравнение Хейвуда [31], который использовал эмпирическое кубическое уравнение для того, чтобы представить данные постоянной жизни. Его уравнение имеет вид
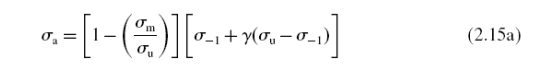
* В то время как обобщенное уравнение Гудмана [3] не указывает симметрию относительно _ m., формулировка в первом Выпуске книги [20] Гудмана представляет уравнения для статической способности груза в условиях динамической теории. Если предполагается, что сила равна при растяжении и сжатии, уравнения указывают, что есть симметрия относительно среднего напряжения. Нехватка данных для отрицательных средних напряжений предотвратила любые существенные дебаты по этой проблеме симметрии. Симметрия уравнения Гудмана и его история обсуждена в [18].
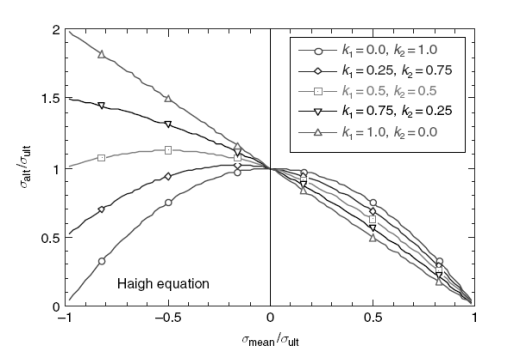
Рисунок 2.30. Диаграмма постоянной жизни для параболического уравнения Хая.
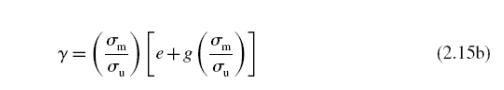
где e и г - или положительные или отрицательные константы. Из-за большого количества сроков наиболее экспериментально определенные данные постоянной жизни могут быть представлены надлежащим выбором констант.
2.8. УРАВНЕНИЕ ДЖАСПЕРА
И практически и исторически значимым является наблюдение Джаспера [32] в 1923, предложившего, чтобы период усталости является связанным с постоянным диапазоном плотности энергии во время цикла в материале, оценивая данные, полученные ранее Хаем. Применяя это понятие к условиям МЦУ, можно предположить, что все усилия и напряжения являются упругими, таким образом, все уравнения представляют просто упругое поведение. Для простой одноосной нагрузки заштрихованная область в иллюстрации 2.31 иллюстрирует схематично сохраненную энергию для случаев, в которых нагрузка просто растяжима (R> 0). Энергия для случая, где R <0, который вовлекает растяжение и сжатие в единичном цикле, иллюстрирована в иллюстрации 2.32 заштрихованной областью. Сохраненный диапазон плотности энергии во время цикла для одноосной нагрузки тогда имеет вид
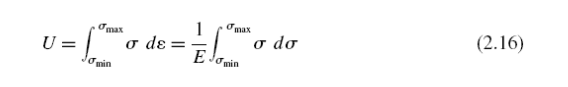
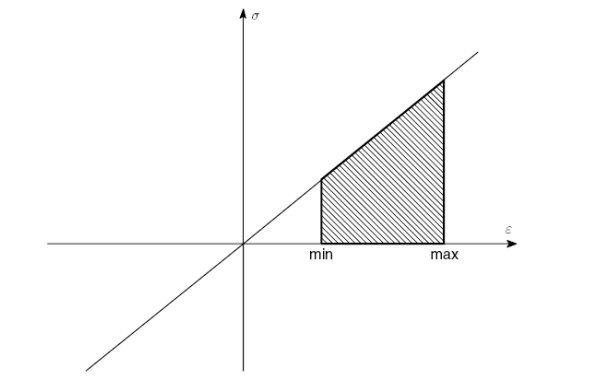
Рисунок 2.31. Сохраненная энергия (заштрихована) для упругой нагрузки при растягивающей усталости ( R> 0).
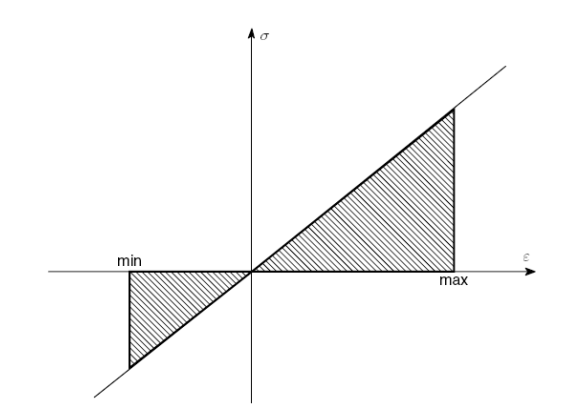
Рисунок 2.32. Сохраненная энергия (заштрихована) для упругой нагрузки при полностью изменяемой усталости (R <0 ).
Интересны является то. что форма диаграммы Хая соответствует постоянному диапазону плотности энергии для любого положительного значения среднего напряжения. Такая диаграмма показанав иллюстрации 2.33, у которой есть та же самая общая форма как для пруткового материала Ti-6Al-4V (иллюстрация 2.34), полученная Максвелом и Николасом [33]. Нужно отметить, что только единственный параметр, _ −1, обязан описывать значения и на оси x, и на оси Y. Этот график (иллюстрация 2.33) является тем же самым типом, который показано ранее как уравнение Джаспера в иллюстрации 2.28, используя типовые числа для пластины титана, где переменные усилия, соответствующие отрицательным средним усилиям, также включены.
Данные по другому высокопрочному сплаву титана, Ti-6-2-4-6, которые имеют место при режиме отрицательного среднего напряжения, показаны в иллюстрации 2.35. Эти данные показывают ту же самую общую тенденцию, как и кривая уравнения Джаспера иллюстрации 2.33 для положительных средних усилий, и имеет форму, подобную той, которая показана впоследствии в иллюстрации 2.36, когда расширяется в режиме отрицательного среднего напряжения. Представление данных для отрицательных средних усилий обсуждено в следующих параграфах.
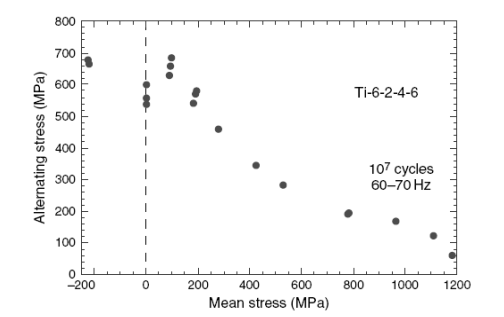
Рисунок 2.35. Диаграмма Хая для Ti-6-2-4-6.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.