Иллюстративный пример поведения S–N, которое неотъемлемо принято в методе Прота, представлен в рисунке 3.1. Под предположением, используемым Протом, что напряжение пропорционально квадратному корню скорости увеличения напряжения, рассчитан числовой пример, предполагая, что напряжение предела усталости равно 500 (произвольные единицы).
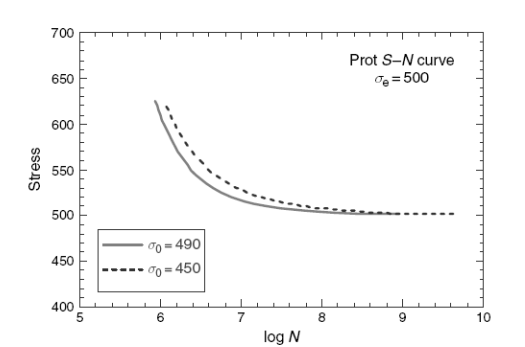
Рисунок 3.1. Иллюстрация числового примера принятого поведения S–N для метода Прота
Для заданных начальных значений 490 и 450, ожидаемое поведение S–N, основанное на предположении Прота, показано на графике В то время как метод предполагает, что стартовое напряжение при постоянном темпе увеличения напряжения находится около предела усталости, вычисления показывают, что есть очень небольшое различие, когда используются два различных значения начального напряжения. С другой стороны, любая другая форма кривой S–N, особенно при больших количествах циклов около предела усталости, не приведет график к прямой линии и таким образом мешает экстраполировать к нулевому темпу увеличения напряжения, от которого определен предел усталости усталостный в методе Прота.
В то время, как беспокойство коаксинге сохранилось в развитии ускоренного теста, метод Прота был подтвержден Вардом и др. [15] на сплаве 4340 стали и, как находили, был применим к черным металлам с четким пределом усталости [16]. Однако, Кортен и др. [16] отмечали, что для черных металлов, которые восприимчивы к коаксингу, процедура Прота заметно поднимает предел усталости по сравнению с полученным обычными методами. В обсуждении их статьи они указали на следующее: “Только если коаксинг отсутствует, и число циклов в каждом шаге является достаточно большим (возможно 107 циклов), становится кажется разумным ожидать, что данные о напряжении перелома, полученные из метода пошагового роста, будут соответствовать пределу усталости, полученному из обычных тестов.” Другая работа Долана и др. [17] показала, что усовершенствование предела усталости под «поднапряжением» зависело, во многом, от относительной разницы между уровнем поднапряжения и усталостным пределом. Перетестирование с низким увеличением уровня напряжения привело к ненормально длинной жизни, но перетестирование со значительными различиями в уровне напряжения не показало очевидного эффекта коаксинга. В структурных сталях Хэмпел [18] заметил, что полностью измененный изгиб усталости на уровне напряжения на 22 % ниже усталостного предела не приводила к развитию ошибочных значений даже при значениях напряжения сверх 107. В более высоких амплитудах напряжения, но все еще ниже усталостного предела, следы промаха происходят только в отдельных кристаллитах. В усилиях выше усталостного предела маркировки промаха были намного более заметными и присутствовали в большом количестве кристаллитов. Но маркировки промаха не обязательно приводят в каждом случае к формированию микро - и макротрещины или к усталостному отказу.
Существование эффекта коаксинга, в то время как он является важным в установлении законности ускоренной процедуры проверки согласно Проту, кажется, нет установленного научного основания. Одно возможное объяснение эффекта коаксинга - то, что это является просто статистическим в природе. Эпремиан и Мэл [19] указывают, что устранение более слабых экземпляров во время тестирования усталости ниже предела усталости оказывает влияние на выбор экземпляров, проверенных на более высоких уровнях напряжения. Из-за статистической селективности экземпляры, впоследствии проверенные выше предела усталости, имеют тенденцию показывать более длительные жизни. Для любого из предложенных объяснений существования явления коаксинга не чувствуется, что коаксинг - реальное явление в сплавах титана и, поэтому, испытательная процедура пошаговой нагрузки, описанная в следующем разделе, действительна для определения предела усталости. Подход Прота, как находили, был разумно надежен для сплава титана [20], и алтернативный пошаговый метод испытаний был подтвержден в нескольких исследованиях, используя Ti-6Al-4V в качестве испытательного сплава [21].
3.3 Процедуры пошагового тестирования
В дополнение к методу Прота, описанному выше, другая форма ускоренного теста, использующего пошаговую нагрузку, была развита Максвеллом и Николасом [22]. При постоянном коэффициенте напряжения экземпляр устает на пределе, как правило, 107 циклов при уровне напряжения ниже, чем ожидаемый предел усталости. После каждого блока 107 циклов напряжение увеличивается на некоторое небольшое количество (приблизительно 5 % в их тестах), пока не происходит отказа при менее, чем при 107 циклах. FLS тогда определяется, используя линейную схему интерполяции, как представлено в следующем уравнении:

где _ e - максимальное усталостная прочность, соответствующая Nlife циклам, _0 предыдущее максимальное напряжение усталости, которое не приводило к отказу, __ увеличение шага максимального напряжения усталости, Nfail - циклы до отказа при напряжении усталости (_0 + __), и Nlife - определенная циклами усталостная жизнь (то есть 106, 107 и т.д.). Линейное понятие интерполяции, воплощенное в уравнении (3.1), было развито из идеи, что накопленное повреждение могло бы быть линейной функцией циклов. Пока не были получены данные для демонстрации этого понятия, использование подобной формулы в уравнению (3.1), основанной скорее на log(N), а не на N, казалось, не имело значения, что было столь же последовательно, как с линейной формулой, сравнивая результаты с интерполированными данными S–N.Для маленьких размеров шага различия, казалось, не были существенными.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.