Есть многие другие представления постоянных значений данных жизни [18], но еще один который достиг некоторой популярности, в 1870-ых известен как Лунхардт–Вэйрауч (L-W) формула, развитая Лаунхардом [24] для положительные значений R, и продолженная Вэйраучем[25] для отрицательных значений R. Используя _ u как предел усталости, уравнении
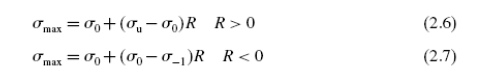
где индекс max относится к максимальному напряжению, а _ 0 и _ −1 относятся к максимальному напряжению при R = 0 и R = − 1, соответственно. Для этих трех формул, измененное уравнение Гудмана,
уравнение Гербера и формулы L–W, экспериментальные данные Вехлера на круппированной стали использовались, чтобы установить наиболее пригодную кривую.
Первый метод представления данных является диаграммой, где максимальное напряжение изображено в зависимости от минимального напряжения, как показано в иллюстрации 2.18. Можно заметить, что формула Лаунхарда–Вейрача(L-W) и парабола Гербера почти идентичны в их представлении данных (не представлено). Прямая линия, приписанная Гудману, делает меньшую работу по соответствующим данным. Линия, представляющая минимальное напряжение, часто изображалась, чтобы указать более низкую границу напряжения для допустимого напряжения. Расстояние между минимальными и максимальными кривыми, в таком случае, допустимое вибрирующее напряжение. В этом и последующих изображениях, кривые являются показательными в условиях нормализованных усилий относительно предельного напряжения. Именно Гудман[20] заявил, что поведение усталости должно зависеть от предельного напряжения, а не от предела упругости.
Другой способ представить данные постоянной жизни является изображением максимального и минимального напряжения против коэффициента напряжения, как показано в иллюстрации 2.19. Отметим, что Гербер и уравнения L–W выглядят снова почти идентичными, в то время как линия Гудмана несколько различна. В этом специфическом изображении линейность линии Гудмана исчезает из-за специфических используемых осей. Это может быть одной причиной, почему этот тип изображения никогда не имел популярности в сообществе усталости.
Третий тип изображения, где максимальные и минимальные усилия изображаются против среднего напряжения, показан в иллюстрации 2.20. Это изображение, вероятно, содержит большинство информации для использования проектировщиком вращающихся машин, потому что средние усилия не только хорошо определены при вычислениях, основанных на центробежных грузах, но могут также хорошо применяться в управлении. Переменные усилия, которые следуют из особенностей вибрации машин, намного меньше управляемы и не так хорошо известны в большинстве случаев. При высоких средних усилиях (высоких значениях R)
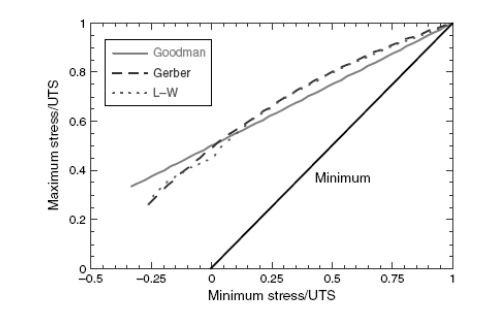
Рисунок 2.18. Максимальное и минимальное напряжение как функция минимального напряжения.
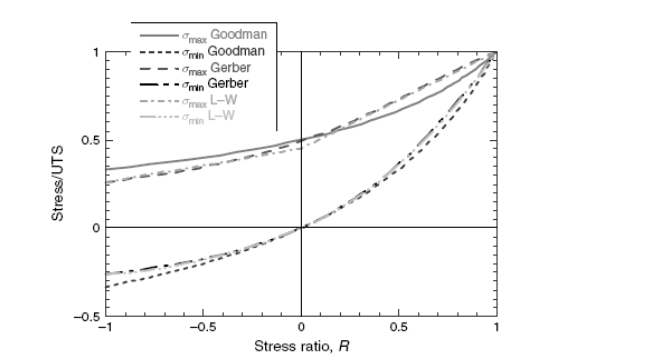
Рисунок 2.19. Максимальное и минимальное напряжение как функция коэффициента напряжения, R.
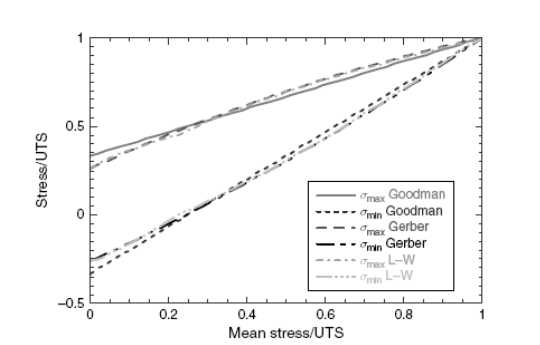
Рисунок 2.20. Максимальное и минимальное напряжение как функция среднего напряжения.
максимальное напряжение может стать управляющим напряжением для проектирования, потому что это может приблизиться к приделу текучести и пределу прочности материала. Различие между двумя кривыми - диапазон напряжения, или дважды переменное напряжение. В этом как и в предыдущих изображениях, Гербер и уравнения L–W выглядят почти идентичными, в то время как линия Гудмана, которая является теперь прямой, отличается немного от других двух уравнений.
Заключительный метод изображения данных является изображением переменного напряжения против среднего напряжения, обычно, но неправильно называемою диаграммой Гудмана, иллюстрация 2.21.
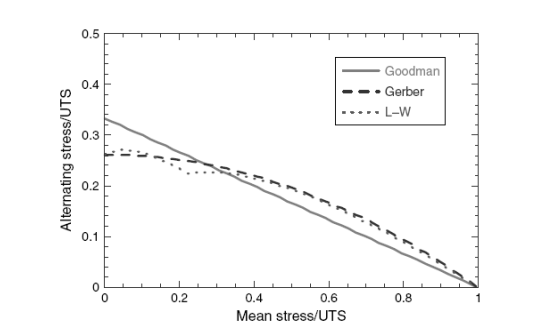
Иллюстрация 2.21. Переменное напряжение как функция среднего напряжения.
По праву так называемая диаграмма Haigh использовалась при выборе метода изображения FLS или данных максимально допустимого напряжения, но использование прямой линии, пригодной к данным все еще остается популярным.
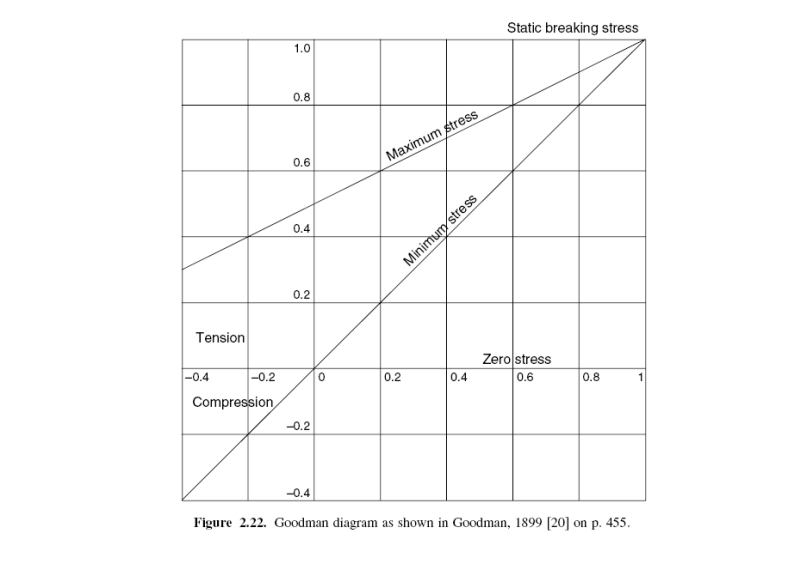
Диаграмма, наиболее близко связанная с этими методами представления предела усталости или данных постоянной жизни, является фактическая диаграмма Гудмана, показанная в иллюстрации 2.22, взятая непосредственно из книги [20] Гудмана. Две кривые, показанные на графике, обозначают максимальное и минимальное напряжение. Они, очевидно, изображены против минимального напряжения, как показано в иллюстрации 2.18, хотя нет никакого обозначения на этом рисунке или на оси Y. Области растяжения и сжатия показывают выше и ниже нулевой линии напряжения. Одним из наибольших значения на этом рисунке, схожим к тому, что можно назвать истинной диаграммой Гудмана, то, что линии, используемые, чтобы представить предел усталости, являются прямыми линиями на этом специфическом рисунке. Это сопоставимо с формирование прямых линий Гудмана, показанных в иллюстрации 2.18 для сравнения.
Уравнения L–W, показанные в предыдущих изображениях, могут также быть исследованы на диаграмме Хая. Для положительных значений R, уравнение (2.6), форма кривой зависит от значения _ 0 - максимальное напряжение при R=0. В безразмерном изображении, где усилия разделены на _ u, кривые, полученные за несколько значений _ 0 / _ u представлены в иллюстрации 2.23. Обозначений “_ 0” относится к нормализованному значению _ Макс при R = 0. Когда _ от 0 до 1, диаграмма Хая представляет точки, где _ Макс = _ u при всех значениях R и является прямой линией, как показано. При других значениях _ 0, линии изогнуты. Только уравнение при положительных значениях R представлено на графике. Линию, представляющую R = 0, показывают в качестве кривой, действительной только справа от этой линии. Теперь очевидно, почему уравнение, действительное сейчас для положительного R, было изменено, чтобы соответствовать данным в −1 <R <0, как представлено в уравнении (2.7). Для этого диапазона R, точки, обозначающие R = 0 и R = − 1, связаны гладкой кривой с небольшим искривлением (здесь не показано).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.