В иллюстрации 2.25 модель A Ходока аппроксимирует данные МЦУ при 59 гц довольно хорошо до значений R = 0.1. Модель Волкера C оказывается выгоднее в переменном напряжении при R = −0.333 и R = 0.1 по сравнению с другими моделями. Обе модели Волкера отклоняются от диаграммы Хая на 59 гц выше R = 0.1 с тех по, как увеличивается среднее напряжение и зависящая от времени усталость механизма уменьшают циклическую способность материала.
Чтобы определить поведение материала с временной зависимостью, два подхода использовались в моделировании поведения разрыва 1484 PWA при 1900 F. Первый подход, более простой из этих двух, предполагает, что только прикладываемое среднее напряжение способствует повреждению разрыва. Этот подход упоминается как Модель разрыва от среднего Напряжения. Второй метод, Модель Совокупного Разрыва, рассматривает суммарное повреждения разрыва от приложенного напряжения по всему циклу усталости.
Рисунок 2.2. Константы при 1900 F модели Волкера

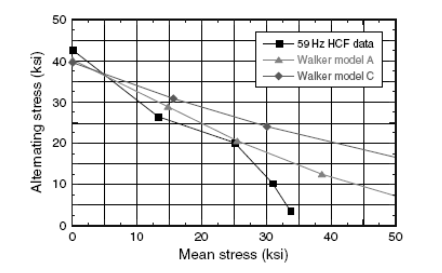
Рисунок 2.25 .Модели A и С Волкера при 59 гц 107 циклов диаграммы Хая.
Модель разрыва от среднего напряжения представлена в качестве выражения в Уравнении (2.11), которое связывает среднее напряжение со временем разрыва. Выражение было получено применением данного отношения к четырем тестам, которые проводились до разрыва. Получающееся уравнение

где _ mean – прикладываемое среднее напряжение в кгс, и tf - время до отказа в часах.
В Модель Совокупного Разрыва повреждение разрыва из-за прикладываемого напряжения объединено по циклам нагрузки, и прикладываемое напряжение выражено как синусоидальная функция, использующая τ как период цикла в часах. Чтобы сделать это, цикл нагрузки разделен на маленькие приращения времени, t. Каждый раз приращение прикладываемого напряжение вычисляется, и определяется соответствующее время до разрыва, с использованием Уравнения (2.10). Повреждение разрыва за приращение времени вычисляется, и части повреждения для t суммируются по циклу нагрузки. Число циклов до отказу может быть вычислено, используя предположение, что отказ происходит тогда, когда повреждение разрыва равняется получившемуся.
Когда R меньше чем ноль, часть цикла нагрузки является сжимающей. Были рассмотрены два сценария, применяющие Модель Совокупного Разрыва: (a) сжимающее напряжение не разрушительно для жизни, и (b) сжимающее напряжение разрушительно для жизни. Таким образом, всего, три модели разрыва рассмотрены: Модель разрыва от среднего напряжения, Совокупный Разрыв без сжимающего повреждения, и Совокупный Разрыв со сжимающим повреждением.
Иллюстрация 2.26 показывает предсказания модели разрыва для постоянной жизни в 107 циклов при 59 гц по сравнению с испытательными данными МЦУ. Обе модели совокупного разрыва аппроксимируют форму диаграммы Хая, основанной на экспериментальных данных. Модель разрыва от среднего напряжения предсказывает среднее напряжение 32.5 кгс независимо от R для 107 циклов в 59 гц как модель просто с временной зависимостью и не рассматривает вклада цикличности в процесс повреждения. Стоит отметить, что циклические модели, иллюстрация 2.25, кажется, делают хорошую работу по
определению данных при низких значениях среднего напряжения.
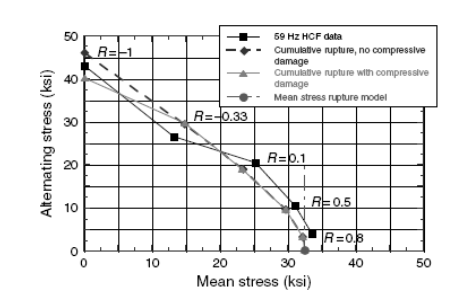
Рисунок 2.26. 1900 'F 107 циклов диаграммы Хая при 59 гц с предсказаниями модели разрыва.
Они получены, однако, от настройки тем очень те же самые данные. Предсказания модели разрыва, с другой стороны, получены строго из данных разрыва без циклического содержания. Способность моделей разрыва представить данные по всему диапазону скупых усилий, иллюстрации 2.26, кажется, указывает что поведение 1484 PWA в 1900 ' F просто с временной зависимостью, или, по крайней мере для того, чтобы моделировать цели, может рассматриваться также. Пример, процитированный выше, указывает на некоторые из рассмотрений, с которыми сталкиваются, готовя данные по диаграмме Haigh и затем пытаясь интерпретировать данные или смоделировать материальный предел усталости, когда материальное поведение включает временную зависимость. Факторы, такие как циклическая частота становятся важными рассмотрениями и, как минимум, должны быть обозначены в заговорах диаграммы Haigh.
2.7. РОЛЬ СРЕДНЕГО НАПРЯЖЕНИЯ НА ДИАГРАММЕ ПОСТОЯННОЙ ЖИЗНИ
Имея дело с данными по FLSs, распространено изображать эти усилия как функцию коэффициента напряжения (R = отношение минимального к максимальному напряжению), или, наиболее обычно, среднего напряжения. Диаграмма Хая, неправильно называемая диаграммой Гудмана, - общепринятая методика представления предела усталости или напряжения предела выносливости материала в условиях переменного напряжения, определенного как половина амплитуды вибрирующего напряжения. Таким образом, максимальное динамическое напряжение - сумма средних и переменных усилий. Для многих вращающихся компонентов среднее напряжение известно абсолютно точно, но переменное напряжение определено менее хорошо, потому что оно зависит от вибрирующих особенностей компонента. Таким образом, диаграмма Хая представляет допустимое вибрирующее напряжение как вертикальную ось, так и функцию среднего или устойчивого напряжения, такую как ось X. В то время как были сделаны попытки определить уравнение, которое лучше всего представляет данные на диаграмме Хая, как описано ранее в этой главе,
изменчивость от материала к материалу, разброса в данных и нехватки достаточных данных во многих случаях предотвращает применяемость уравнения к таким данным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.