Один метод развития диаграммы Хая, которая представляет материал в детали, должен развить данные по фактическим аппаратным средствам. В этом случае, комбинация нагрузки НЦУ и МЦУ, или общей нагрузки спектра, могла использоваться, чтобы получить единственную точку на диаграмме. Соединение этой точки с любой другой точкой на изображении Хая не имеет никакого физического основания и никакого значения и, наиболее вероятно, будет вводить в заблуждение. Если данные не получены при просто нагрузке МЦУ без других механизмов образования повреждения, у диаграммы Хая нет никакого основания для использования при проектировании, и данные лучше использовались бы табличным способом для определенных условий проектирования. Существенное значение имеет то, что попытка смешать данные МЦУ и НЦУ по единственной диаграмме опасна, потому что физические процессы различны. НЦУ обычно имеет высокую амплитуду, низкочастотную нагрузку, которая приводит к появлению трещин на ранней стадии жизни и значительному распространению излома. Именно эта точка зрения сделала возможным успешное применение устойчивости к повреждению, используя механику перелома при проектировании. МЦУ, с другой стороны, вообще имеет низкую амплитуду, высокочастотную нагрузку, со значительной частью жизни, потраченной на образование трещины. Взаимодействие двух типов нагрузок, поэтому, может повлечь процесс образования и роста трещины и роста при НЦУ, и последующего распространения при МЦУ. Диаграмма Хая показывает только часть инициирования МЦУ при отсутствии начальных трещин и, поэтому, не имеет никакого значения при объединенной погрузке НЦУ–МЦУ. Эта тема обсуждена подробно позже в Главе 4.
2.5. УРАВНЕНИЯ ДЛЯ ДИАГРАММ ПОСТОЯННОЙ ЖИЗНИ
Чтобы иллюстрировать различные методы представления данных графически, мы рассматриваем несколько моделей или уравнений, которые использовались традиционно для диаграмм постоянной жизни [18]. Первым и, вероятно, самым популярным является линия Гудмана, или уравнение Гудмана, более часто называемаю как прямая линия в измененной диаграмме Гудмана. Это было фактически предложено Хаем [19] в 1917 как метод для того, чтобы представить постоянную жизнь, таким образом диаграмма, которая изображает переменное напряжение как функцию среднего напряжения, не является действительно диаграммой Гудмана, а является диаграммой Хая, и также упомянута всюду в этой книге. В то время, как некоторые из уравнений, которые будут обсуждены позже, используются, чтобы представить данные FLS а изображениях диаграммы Хая, многие соответствия данным были вообще установлены эмпирически и не имеют никакого научного основания. Однако, некоторые из самых ранних работ попытались установить физических зависимости для усталости [18]. Гудман [20] предложил использование “динамической теории”, которую объясняет подробно Фидлеру[21], где предполагается, что вибрирующие нагрузки оказывают то же самое влияние на материал как внезапно приложенная нагрузка. Таким образом, вибрирующие нагрузки, как полагают, мгновенно производят усилия, которые удваиваются, если они были применены медленно. Последствие этого - то, что сумма среднего напряжения и дважды переменного напряжения не должна превысить статический предел прочности материала, чтобы иметь бесконечную жизненную усталость. Это приводит к прямой линии на диаграмме Хая, когда допустимое переменное напряжение взято равным половине предела прочности (см. иллюстрацию 2.17). Интересно то, что Гудман предложил такое уравнение в качестве “очень легкого для изображения, кроме того, простого в запоминании” [20]. Он также отмечал, что, "допустимы ли предположения о теории или не являются настоящим нерешенным вопросом.” В то время как динамическая теория была проста, было замечено, что экспериментальные данные относительно всех материалов не соответствовали теории.
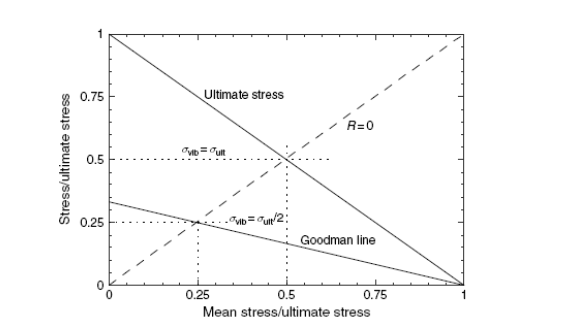
Рисунок 2.17. Схематичное изображение диаграммы Гудмана, иллюстрирующая допустимое вибрирующее напряжение.
При лучшем обращении к истинному поведению материала, полностью измененное знакопеременное напряжение было принято как эмпирическая константа, а не половина предела прочности. Что первоначально назвали “измененной диаграммой Гудмана” с использованием прямой линии пригодна на диаграмме Хая, основанной на экспериментально решительном полностью измененной точке(ах) данных нагрузки. Так называемое уравнение Гудмана (или Измененное уравнение Хозяина), представленное в следующих изображениях имеет форму

где индексы a, м, и u относятся к знакопеременному, среднему, и предельному усилиям соответственно, а _ −1 представляет экспериментальную значение переменного напряжения при полностью измененной циклической нагрузке (R = − 1). Дополнительная форма уравнения Гудмана - прямая линия, которая пересекает ось среднего напряжения в напряжении текучести, _ y, в противоположность окончательному напряжению. Такое представление диаграммы постоянной жизни предела усталости было предложено Содербергом [22], и уравнение называют в честь него в литературе.

Возможно лучше представляет экспериментальные данные параболическое уравнение, приписанное Гербером [23], использовалось которое в форме:
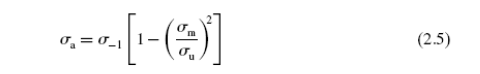
Суммируя имеющиеся данные предела усталости по диаграмме Хая, Форреста15] полученные путем наблюдения за большим массивом данных относительно податливых металлов, полечаем что 90% лежит выше линии Гудмана, а две трети между линией Гудмана и параболой Гербера. Он заключил, что, "хотя не 100% надежная, линия Гудмана может, поэтому, быть рекомендована как полезное рабочее правило в проектировании, когда данные об усталости переменного напряжения при сжатии не доступны.” Он предостерег, однако, что эти заключения не обязательно относятся к деталям, содержащим концетраторы напряжения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.