Экспериментальные данные для отрицательного среднего напряжения были получены Николасом и Максвелом[29], которые не показали их ни следовал за уравнением Джаспера, ни SWT или уравнениями Волкера(см. иллюстрацию 2.28). По этой причине, они предложили модификацию уравнению Джаспера, которое рассматривает сохраненную энергию различных напряжений, которые происходят из-за усилий сжатия. Хай[30], в 1929, в обращении к результатам Баушингера 1915 года и 1917 года, отмечает, что “этот ряд тестов … было вероятно первым, который когда-либо показал какое-либо различие между действиями напряжения и кратковременного воздействия относительно усталости.”* Что касается данных по военно-морскому руководству, он указал, “В этом металле, как во многих других, напряжение имеет тенденцию уменьшать предел усталости, в то время как толчок увеличивает сопротивление усталости.” После этой идеи Николас и Максвелл постулировали, что сохраненная плотность энергии в цикле не способствует
процессу усталости так сильно, когда усилия являются сжимающими как тогда, когда они находятся в растяжении. Проявляя самый простой подход, где сжимающая энергия напряжения вносит фракцию, α, по сравнению с сопоставимой энергией при растяжении, тогда полная эффективная энергия была сформулирована в следующем виде, где α<1:

В использовании этого уравнения условия энергии, соответствующие отрицательным усилиям, должны быть изменены коэффициентом α. Введение константы имеет эффект изменения формы уравнения Джаспера, как показано в иллюстрации 2.37 для нескольких значений константы α. Усилия на обоих осях - те же самые, как используемые в иллюстрации 2.28. Константа α тогда использовалась, чтобы соответствовать фактическим экспериментальным данным, полученным для значений R <−1, соответстующих отрицательным средним усилиям.
Используя подделанный листовой материал Ti-6Al-4V, тесты усталости проводились при условиях постоянное амплитуды напряжения по широкому диапазону коэффициента напряжения от 0.8 до −3.5. Минимальное значения коэффициента напряжения, для которого могли быть проведены тесты, было ограничено напряжением текучести материала. Чтобы установить напряжение предела усталости, соответствующее 1077 циклам, образцы были проверенным воздействию тестов на усталость с использованием пошаговой нагрузки Максвола и Николаса [33], которые обсужден в следующей главе.
Экспериментальные значения для FLS, полученные для широкого диапазона значений R, представлены в форме диаграммы Хая в иллюстрации 2.36. Данные показаны как МL на графике, и объединены с ранее неопубликованными данными от Союзнических Сигнальных Механизмов (ASE), теперь Honeywell, на том же самом материале. Лучший описание данных, используя измененное уравнение Джаспера также показано на графике. Константа α в измененном уравнении Джаспера (2.22) была получена как 0.287, соответствуя к экспериментальным данным, полученным для
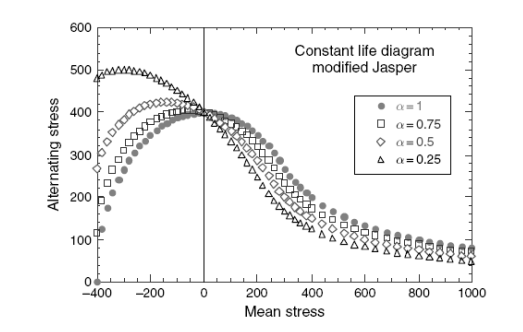
Рисунок 2.37. Диаграмма Хая для измененного уравнения Джаспера при различных значениях α.
R = 0.8 до R = − 3.5. Взвешенная энергия была получена для каждой точки данных как функция переменной α в Уравнении (2.22), и процента ошибки наименьших квадратов между средней энергией всех точек данных и индивидуальными значениями энергии был минимизирован. Чтобы представить результирующее измененное уравнение Джаспера, напряжение, соответствующее средней энергии при R = − 1, должно было быть получено и, как обнаружили, было равно500 MPa.
При рассмотрении методов того, чтобы представить данные предела усталости на диаграммах постоянной жизни, Максвелл и Николас [33] отметили, что диаграмма Хая – это та диаграмма, которая достигла наибольшей популярности. В обзоре этих диаграмм авторы предположили, что самая важная информация для проекта это не только переменное напряжение, но также и максимальное напряжение, как представлено в изображении против среднего напряжения (см. иллюстрации 2.20 и 2.21 выше). В результате, диаграмме было предложено название диаграмма Николаса-Хая [33], которая, как отмечает история, не получившая абсолютно никакого принятия или признания от технического сообщества и бывшая недолгой, никогда не упоминалась снова до настоящего момента. Для пользы потомства рассуждения о ранее предложенной диаграмме, и что еще более важно, значение максимального напряжения в диаграммах постоянной жизни, обсуждены далее.
Представление и переменного напряжения, и максимального напряжения против среднего напряжения, первоначально названное диаграммой [33] Николаса-Хая, представлено за возможный значимый дублирования прошлых усилий так же как запутывающих будущих историков. Этот изображение может использоваться, чтобы представить данные для того, чтобы разрабатывать проект двумя способами. Для низких значений среднего напряжения, или низких R (R <0.5), переменное напряжение - решающее допустимое значение, особенно для того, чтобы применять турбины, в которых средние усилия относительно предсказуемы и обычно хорошо определяются. Для высоких значений среднего напряжения, или высоких R (R> 0.5), максимальное напряжение становится более критическим параметром при проектировании. Здесь предлагается, чтобы предел безопасности был наложен на оба параметра (переменное напряжение и максимальное напряжение), чтобы обеспечить безопасность проекта. Диаграмма Николаса-Хая была попыткой представить данные в форме, которая позволит проектировщику признавать важность обоих параметров. Такое представление, возможно, не совсем новое, но в него были включены следующие особенности:
a. Это - метод представления экспериментальных данных. Нет никакого уравнения или формулы, предназначенной или подразумеваемой, чтобы представить данные.
b. Нет никакого определенного значения точки пересечения оси Y (нулевое среднее напряжение, или R = − 1), которое связано с любой материальной собственностью, такой как предел текучести или разрушающее напряжение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.