Термин "среднее напряжение" использован в диаграмме Хая, хотя “усредненное напряжение” или “равномерное напряжение” также обычно используются. Равномерное напряжение – это уровень напряжения, на который добавлены вибрирующие усилия, но диаграмма Хая представляет только амплитуду постоянной нагрузки и не представляет условие, где добавлена амплитуда переменной нагрузки или НЦУ. Далее, обычная диаграмма Хая действительна только для частоты, в которой были получены данные, которые обычно являются меньшими, чем те, которые используются в проекте. Это также не действительно, для использования диаграммы Хая для случайной вибрирующей нагрузки без существования утвержденной совокупной модели повреждения для МЦУ.
Хотя большинство данных S–N и кривых получено при условиях постоянного значения R, некоторые эксперименты, особенно при вращающихся компонентах, проводятся при условиях постоянного среднего напряжения. Различие между постоянным R и постоянным средним напряжением иллюстрировано схематично на рисунке 2.13. Вспомните, что R - отношение минимума к максимальному напряжению. Для циклов постоянного среднего напряжения у каждого будет различное значение R. Наоборот, у циклов с постоянным R будут различные средние усилия при различных значениях диапазона напряжения или максимального напряжение. Рассмотрим материал, чье поведение S–N описано уравнением вида
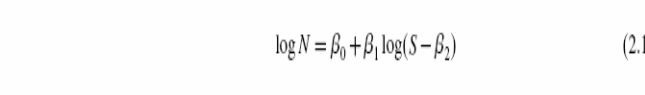
где _0 и _1 соответствуют параметрам, принятым в иллюстративных целях, являющимися независимыми от R. Отметим, что это - детерминированная модель и _2 представляет предел усталости.
∗ Диаграмма постоянной жизни или предела усталости, которую мы именуем как диаграмма Хая, часто неправильно названная диаграммой Гудмана, была упомянута в ранней литературе как диаграмма [15] R–M или, попеременно, как диаграмма [16] R \ M. Там, R относится к диапазону напряжения (дважды переменное напряжение), в то время как М относится к среднему напряжению. Очевидный беспорядок с отношением напряжения, R, вероятно привел к другим особенностям, таким как (неправильная) диаграмма Гудмана, диаграмма Хая. или переменная по отношению к скупой диаграмме напряжения.
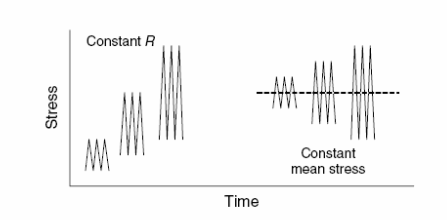
Рисунок 2.13. Схематичная иллюстрация циклов при постоянном R и постоянном среднем напряжений
Чтобы быть совместимым с порогами усталости, типично являющимися линейно уменьшающимися функциями R, мы произвольно выбираем следующие отношения, чтобы представить усталостный предел:
_2 = 150−100R (2.2)
В этом числовом моделировании, S взята как амплитуда напряжения в произвольных единицах. Используя константы _0 = 10 и _1 = −2 , построены кривые S–N как показано в иллюстрации 2.14.
Если то же самое уравнение использовать, чтобы построить кривые S–N для постоянных значений среднего напряжения, получаются такие кривые как показано в иллюстрации 2.15. Численные значения были взяты только для значений R от 0 до 1. Таким образом, диапазон средних напряжений, где составляющая кривой S–N по диапазону регистрации N между 5 и 10 для этого числового представления, несколько ограничен. Для этой частной иллюстрации кривые постоянного среднего напряжения имеют ту же самую общую форму как кривые постоянного R, но, кажутся более связанными вместе. Однако, этот аспект представления кривых очень зависит от формы кривых S–N для конуоретного материала.
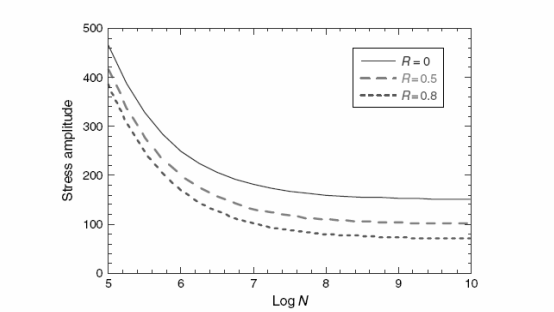
Рисунок 2.14. S–N кривая для гипотетического материала при постоянном R
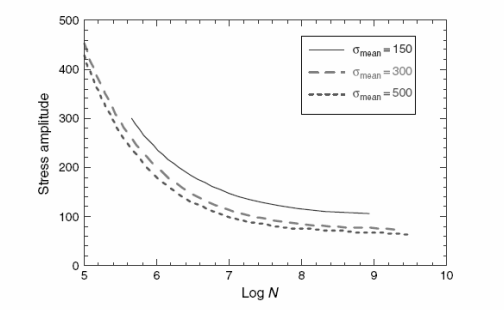
Рисунок 2.15. S–N кривая при постоянных значениях среднего напряжения
Пример данных, полученных для нескольких значений среднего напряжения, представлен в иллюстрации 2.16 для инструментальной стали SKH51 [17]. В то время как экстраполяция и искажение наборов данных часто вынуждены, данные в иллюстрации 2.16 иллюстрируют те единственные параметры, с которыми объединены наборы данных, и не всегда жизнеспособны, потому что индивидуальные группировки данных, при постоянном среднем напряжении как в этом случае, не приводят к хорошими тенденциями. В этом случае, наклоны на кривых S–N не изменяются непрерывно с увеличением или уменьшением в среднем напряжении. Далее, циклы до отказа, где кривые становятся горизонтальными, указывая предел усталости, также не следуют за последовательной тенденцией. Преобразование этого набора данных в тот, где коэффициенты напряжений R, являются постоянными, не очень практичен, если формулы существуют для интерполяции или экстраполирования данных при постоянном R. Эта тема затронута далее в Главе 8.
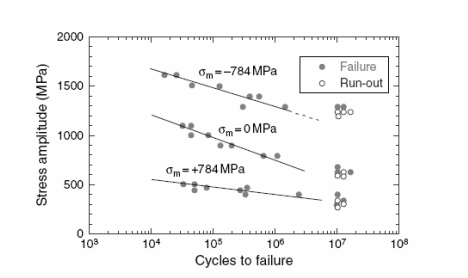
Рисунок 2.16. Данные S–N для инструментальной стали SKH51, полученные при постоянных средних напряжениях [17].
В то время как большинство данных во многих случаях получено при R = −1, представляя собой полностью измененную нагрузку со значительным напряжением, применение диаграммы Хая к МЦУ часто вовлекает условия высоких значений R, таких как 0.7–0.9. Эти условия представляют собой высокие средние напряжения с маленькими, добавленными вибрирующими усилиями. Часто существует очень немного данных, доступных в этой области, как экстраполяция данных от низких значений R, так и предположения, что статистические распределения данных - те же самые, что и при высоких R, поскольку они существуют при низких R, сомнительны.
Качество материала - другой параметр, который нужно рассмотреть, используя диаграмму Хая в процессе проектирования. То, что данные получены в лаборатории на гладких экземплярах, имеют термообработку, мехобработку, микрострукутру, класс чистоты поверхности, и размер экземпляра - нужно все рассмотреть, применяя данные к структурным элементам. Возможно, единственная самая критическая проблема в использовании диаграммы Хая - степень начального или вызванного обслуживанием размера повреждения, который может содержаться в материале детали, когда такое повреждение не присутствует в материале, используемом для базы данных. Если, например, микротрещины или другое повреждение развивается при обслуживании, то диаграммы Хая ни имеет никакого значения для этого материала, потому что она представляет это как "хороший" или неповрежденный материал. Методология проектирования, которая рассчитывает развитие повреждения из любого другого источника, нежели постоянная амплитуда нагрузки МЦУ, должна использоваться, чтобы описывать различное состояние материала. Например, если трещины развиваются из-за НЦУ, то устойчивость материала могла бы быть оценена, используя механику перелома и понятие порогового фактора интенсивности напряжения. У диаграммы Хая нет никакой законности при этой ситуации. Именно к подобным проблемам обращаемся в оставшейся части этой книги.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.