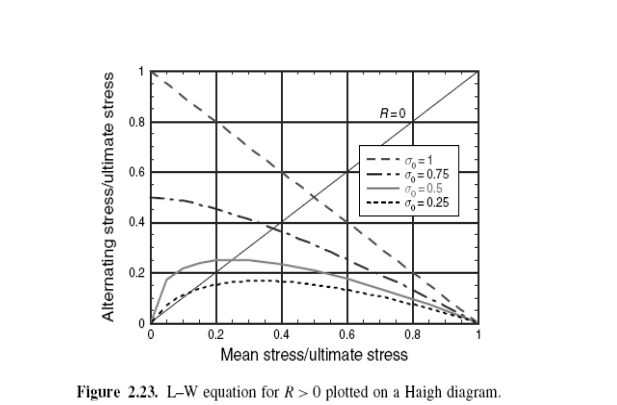
Кривая на иллюстрации 2.23 для _ От 0 до 0 ' 5 проходит точку оригинального уравнения Гудмана при R = 0, где _ Макс = 0 ' 5 _ u. Кривая ближе к параболе Гербера, чем прямая линия в той области, но, возможно, не имеет большего физического значения, чем другие два представления экспериментальных данных.
Можно заметить, что развитие методов представления данные предела усталости базировалось на комбинации математически простых форм, так же как на графических представлениях. В то время как, казалось, было физическое основание некоторого вида из всех подходов, объединенных с простотой, нужно указать, что выборы методов представления данных тщательно исследовались в течение их развития. Особенно проницательный пример такого критического анализа был сделан в 1880 году[26], хотя подобные слова будут одинаково действительны сегодня. Комментируя формулу W–L, используемую, чтобы представить данные Вехлера, Смит пишет: “Фактически, формула, кажется, больше продукт чистого воображения, чем базирования на экспериментах.” Он далее указывает, что “формула может, конечно, быть соответствующей чрезвычайными результатами любого определенного набора экспериментов. Я смею утверждать несколько другое, хотелось бы знать, соответствует ли эта формула, с даже грубой степенью приближения, промежуточным результатам.” Он продолжает по вопросу “любая из параболической кривой _ _ _. является правильной кривой _ _ _” и подводит итог: “я утверждаю, что надлежащая полезная вещь не должна выдумать правила из воображения, но должна упорно продолжать заниматься осторожными и терпеливыми экспериментами, и наблюдать узко и изучить и проанализировать приближенных результаты, пока не показаны истинные близкие законы напряжения и усталости металлов.”
2.6. Диаграмма Хая при повышенной температуре
В заключении программы МЦУ о поведении материала [27], диаграмма Хая была построена для монокристалического сплава PWA 1484 при жизни в 107 циклов, основанных на данных 1900 ' F S–N тестов. Поведение напряженного существования было характеризовано для каждого коэффициента напряжения, R, в обозначениях переменного напряжения _ используется соотношение типа:

Данные использовались только от <001> ориентируемый образец за исключением восьми экземпляров, ориентируемых в <001+15>, которые были проверены при R = 0.8. <001+15> ориентируемое падение данных на вершине <001> данные и следовательно были включены в набор данных, чтобы характеризовать R = 0.8 поведений жизни напряжения. Значения для констант k и м для каждого проверенного значения R показаны в Табице 2.1.
Используя эмпирические отношения S–N, кривая экстраполировалась к более длинным жизням, и Диаграмма Хая была построена, соответствуя жизни 107 циклов, как показано на иллюстрации 2.24.
Диаграмма Хая показывает способность МЦУ1484 PWA при 1900 ' F. Форма диаграммы довольно обычна для низких значений среднего напряжения.
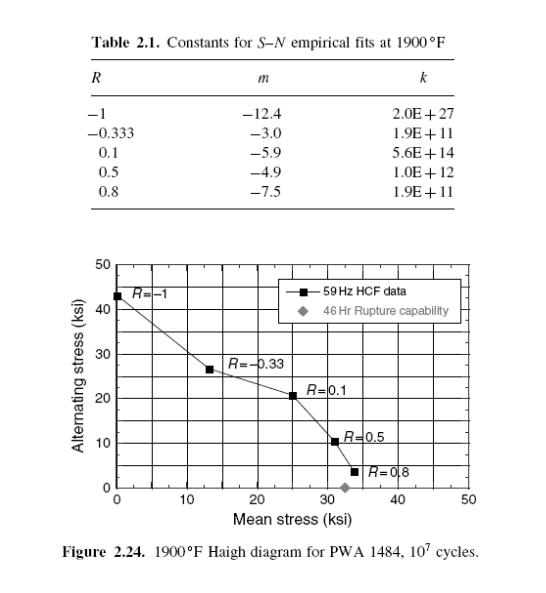
Постепенное уменьшение способности в переменном напряжении сопровождается увеличением допустимого среднего напряжения. Однако, выше R = 0.5, способность переменного напряжения понижается быстро, поскольку приближается к способности разрыва напряжения. Свойство напряжения разрыва может быть представлено как асимптота в R = 1 при воздействии в течение 46 часов 107 циклов в 60 гц (который был оригинальной запланированной частотой). Для этого материала есть как зависимые от цикла, так и зависимые от времени модели отказа, прежний обычно связывался со значениями переменного напряжения и последнего, связанного прежде всего со средним напряжением.
Чтобы составить более сложное поведение усталости, использовалась модель Волкера, для представления поведения материала. В модели Волкера эквивалентное переменное напряжение определено, чтобы принять во внимание различные условия среднего напряжения. Это эквивалентное переменное напряжение, _ equivalent_alt, тогда используется в отношениях закона о власти жизни напряжения как показано ниже:

где эквивалентное переменное напряжение получают из:
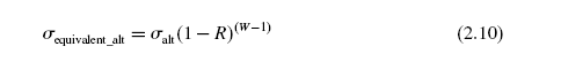
Экспонента Волкера, w, была определена из данных от нескольких значений R и повторялась до тех пор, пока стандартная ошибка в прогнозируемой жизни не была минимизирована. Модель Волкера разрушилась ответ S–N по диапазону отношений напряжения. В то время как экспонента Волкера обычно определяется по полному диапазону данных коэффициента напряжения, которые доступны, в этом случае R = − 1 к R = 0.8, цель здесь состояла в том, чтобы охватить только те экземпляры, которые терпят неудачу в обычном режиме усталости. Фрактография показала, что отказ был во власти усталости только при в условиях низких коэффициентах усталости или низком среднем напряжении.
Были рассмотрены два подхода, соответствующе модели Волкера. Первый (называемый “модель A Волкера” в дальнейшем) использовал данные МЦУ при 59 гц при всех R ≤ 0.1. Второй подход (модель Волкера C) был исследован потому что несмотря на основанное на усталости появление экземпляров в R = 0.1 проверенный в 59 гц, предыдущая работа показала, что процесс с временной зависимостью также присутствует при этом испытательном условии [27]. При постоянном напряжении при R = 0.1, усталостная долговечность в циклах увеличилась, поскольку частота была увеличена с 59 до 900 гц. Линия с наклоном 1:1, аппроксимирующая данные, довольно хорошо указывала весь процесс временной зависимости до самой высокой проверенной частоты в 900 гц. Переход к независимому от времени поведению с циклами к отказу, поддерживающему постоянный уровень, может существовать только вне 900 гц или мог произойти вне этой частоты. В результате оценка образца Волкера при чистой МЦУ может быть затронута при использовании более низких данных при 59 гц. Поэтому второй подход использовал только высокочастотные данные (370-400 гц) при R = 0.1 в комбинации с данными при 59 гц при R = − 1 и R = − 0.333, чтобы представить независимое от времени поведение. Постоянные модели Волкера для каждого подмножества данных МЦУ представлены в таблице 2.2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.