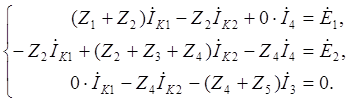Домашние задания по расчету электрических цепей: Методические указания, страница 5

                                        (2.3)

Подставим значения параметров элементов и запишем систему уравнений (2.3) в матричной форме:

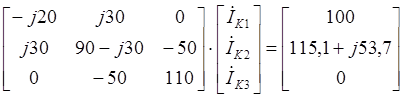                            (2.4)

Составленное матричное уравнение (2.4) решаем с помощью прикладной программы MathCAD и находим комплексы контурных токов. На основании комплексов контурных токов вычисляем токи во всех ветвях.

Используя закон Ома в комплексной форме, определяем комплексные амплитуды напряжений на элементах схемы.

Записываем все токи и напряжения в алгебраической и показательной формах.

Используя значения комплексных амплитуд, записываем их мгновенные значения.

Результаты вычислений оформляем в виде таблицы.

Ток	Форма записи токов
	Арифметическая	Показательная	Тригонометрическая	Мгновенные значения

Сравниваем полученные п.1 и п.2 результаты.

3. Составление и решение системы уравнений по методу узловых потенциалов.

В схеме рис. 2.1имеются три узла. Принимая потенциал узла 3, равным нулю, т.е. , составим исходную систему уравнений:

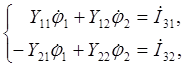                                                       (2.5)

где

                    

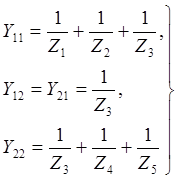
-узловые проводимости исследуемой схемы;

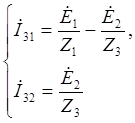
‑ узловые токи.

Подставляя численные значения элементов схемы, получим:

,

,

,

,

.

После подстановки числовых значений система уравнений (2.5) принимает вид:

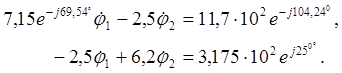
Решаем систему уравнений с помощью определителей. Находим комплексы узловых потенциалов: 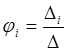, где  является определителем узловых проводимостей, -алгебраические дополнения определителя.

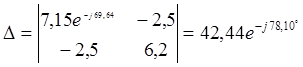
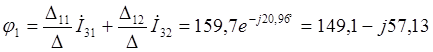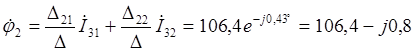В

 В

Находим комплексы токов в ветвях, учитывая, что :

,

,

,

,

.

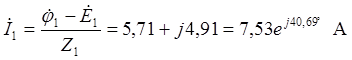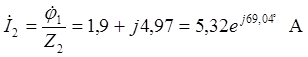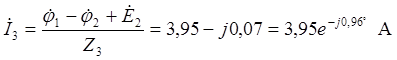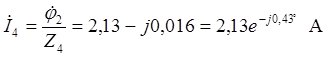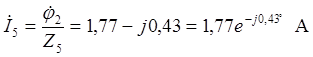Используя закон Ома в комплексной форме, определяем комплексные амплитуды напряжений на элементах схемы.

Записываем все токи и напряжения в алгебраической и показательной формах.

Используя значения комплексных амплитуд, записываем их мгновенные значения.

Результаты, полученные методом узловых потенциалов, сравниваем с результатами, полученными в п.1 и 2.

Результаты вычислений оформляем в виде таблицы.

Ток	Форма записи токов
	Арифметическая	Показательная	Тригонометрическая	Мгновенные Значения

4 Расчет активных и реактивных мощностей.

Определим активную, реактивную и полную мощности, потребляемые цепью. Для этого найдем в начале комплексную мощность источников цепи

.

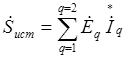Подставляя численные значения, получим

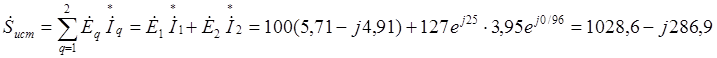ВА

Полная мощность определяется как модуль комплексной мощности

 ВА.

Полная мощность состоит из активной и реактивной составляющих

откуда найдем активную и реактивную мощности как вещественную и мнимую (соответственно) части комплекса полной мощности:

 Вт,

ВАр.

Для составления баланса мощностей найдем комплекс полной мощности приемников

 

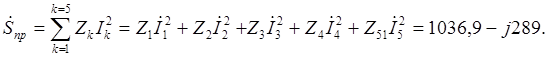
Полная мощность состоит из активной и реактивной составляющих

Проводим оценку баланса:

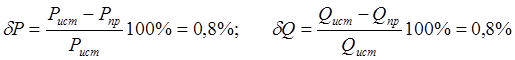
Полученная погрешность находится в пределах погрешности вычислений. Таким образом, баланс активных и реактивных мощностей в схеме соблюдается.

5. Определение показаний приборов.

Амперметр показывает действующее значение измеряемого тока I_A=I₂=5,32 A. Вольтметр – действующее значение измеряемого напряжения U_V=U₄=106,4 В.

Показание ваттметра определяется произведением действующих значений измеряемого напряжения и измеряемого тока, умноженного на косинус угла сдвига фаз между ними: .

6. Построение векторной диаграммы токов и напряжений.

Для построения может быть использована любая форма записи комплексных чисел (рис.2.2). Диаграмма токов должна удовлетворять уравнениям по первому закону Кирхгофа, диаграмма напряжений - уравнениям по второму закону Кирхгофа. Диаграмму строим на миллиметровке, используя масштабы, соответствующие ГОСТ: М (A/см, В/см) = 0,2; 0,5; I; 2; 5; 10; 20 ... (Диаграммы токов и напряжений выполняем разными цветами).

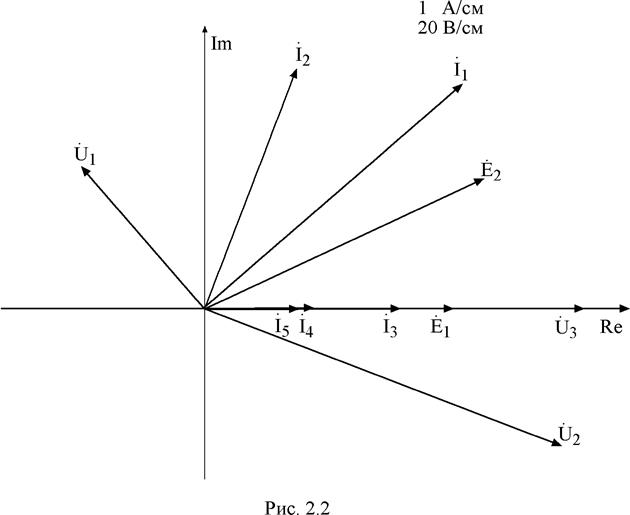9.  Определение тока i₅, методом эквивалентного генератора.