Требуется:
1. Считая фильтр симметричным и нагруженным на повторное сопротивление, найти параметры элементов фильтра. Повторное сопротивление на частоте согласования принять равным Rн. Для фильтров частота резонанса последовательного или параллельного контура должна располагаться в полосе затухания и совпадать с ближайшей к границе полосы (только для режущих фильтров) частотой сигнала (гармоники), имеющейся в спектре напряжения генератора.
2. Для полученного фильтра найти и построить графики зависимости модуля коэффициента передачи и повторного сопротивления от частоты.
3. Нагрузив на постоянное активное сопротивление -Rн фильтр, рассчитанный в п.1, рассчитать его частотные передаточные функции по напряжению и по току, представив их в виде отношения полиномов. С применением прикладных программ, на компьютере рассчитать амплитудно-частотную и фазочастотную характеристики нагруженного фильтра. Построить графики этих характеристик.
4. Найти границы полосы пропускания по напряжению и току и сравнить их друг с другом и с заданной полосой пропускания.
5. Для фильтра п.2 на частоте согласования рассчитать параметры Г- образного согласующего четырехполюсника, обеспечивающего передачу максимальной мощности к нагрузке. Заменить последовательно включенные согласующий четырехполюсник и фильтр эквивалентным четырехполюсником. Найти на частоте согласования модуль коэффициента передачи по напряжению эквивалентного четырехполюсника, определив необходимые для этого постоянные эквивалентного четырёхполюсника. Полученный коэффициент передачи сравнить с аналогичным коэффициентом, рассчитанным в п.1 и 2.
Методические указания.
Рассмотрим особенности выполнения задания на примере расчета фильтра варианта 32. Схема симметричного фильтра приведена на рис. 4.3.
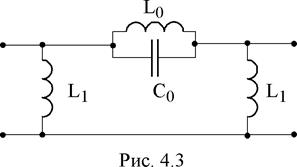
1. Найдем комплексное сопротивление Z0 продольной ветви фильтра и проводимости Y1 поперечных ветвей фильтра
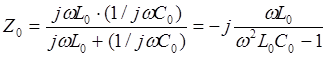 ,
, ![]() , (4.1)
, (4.1)
на основании которых вычислим постоянные четырехполюсника. Для П-образной схемы замещения симметричного четырехполюсника постоянные фильтра
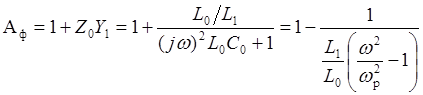 ,
(4.2)
,
(4.2)
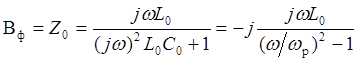 ,
(4.3)
,
(4.3)
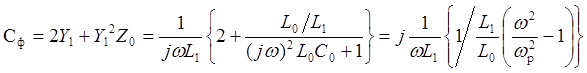 ,
(4.4)
,
(4.4)
где ![]() (4.5)
(4.5)
‑ частота резонанса параллельного контура L0C0.
Границы полосы
пропускания симметричного реактивного фильтра, нагруженного на повторное
сопротивление, определяются из условия ![]() .
Приравнивая единице постоянную Аф, определяем верхнюю границу
.
Приравнивая единице постоянную Аф, определяем верхнюю границу
![]() . Второе условие Аф= -1 приводит
к уравнению
. Второе условие Аф= -1 приводит
к уравнению
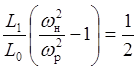 .
(4.6)
.
(4.6)
Характеристическое
сопротивление ![]() . Используя (4.3) и (4.5),
находим
. Используя (4.3) и (4.5),
находим
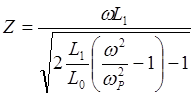 .
(4.7)
.
(4.7)
В соответствии с исходными данными![]() ,
, ![]() ,
, ![]() ,
, ![]() . Уравнения (4.5), (4.6) и (4.7) образуют
систему для определения величин элементов L0 , C0 и L1 фильтра
. Уравнения (4.5), (4.6) и (4.7) образуют
систему для определения величин элементов L0 , C0 и L1 фильтра
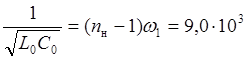 ,
(4.8)
,
(4.8)
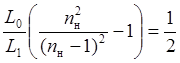 ,
(4.9)
,
(4.9)
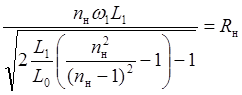 .
(4.10)
.
(4.10)
Из выражения (4.9) найдем L1/L0= 2,13 и подставим его в (4.10), откуда получаем L1=0,116 Гн. Далее рассчитываем L1=0,054 Гн и, из формулы (4.8), находим С0= 0,1063 мкФ.
Считая фильтр
нагруженным на характеристическое сопротивление, найдем модуль коэффициента
передачи в полосе затухания ![]()
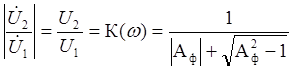 , где постоянная Аф фильтра определяется
выражением (4.2).
, где постоянная Аф фильтра определяется
выражением (4.2).
Модуль коэффициента
передачи в полосе пропускания равен единице. График зависимости ![]() представлен на рис. 4.4. Замечаем, что на
частоте резонанса (4.5) параллельного контура коэффициент передачи фильтра
равен нулю.
представлен на рис. 4.4. Замечаем, что на
частоте резонанса (4.5) параллельного контура коэффициент передачи фильтра
равен нулю.
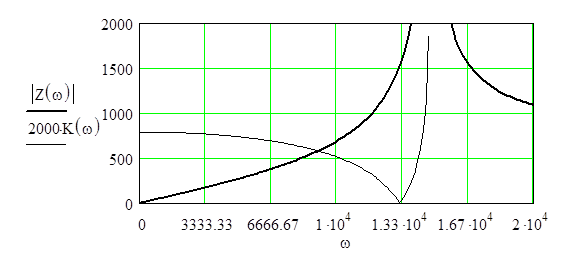 |
Характеристическое
сопротивление рассчитывается по формуле (4.7). В полосе пропускания повторное
сопротивление есть вещественная величина (активное сопротивление), а в полосе
затухания - мнимая величина (емкостное сопротивление). Зависимость модуля
характеристического сопротивления от частоты изображена на рис.4.4. Заметим,
что на частоте согласования ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.