Домашние задания по расчету электрических цепей: Методические указания, страница 18

-  емкость заменить последовательным соединением операторного сопротивления  и добавочного источника, ЭДС которого направлена противоположно напряжению  и равна .

Для рассматриваемой цепи операторная схема изображена на рис. 6.6.

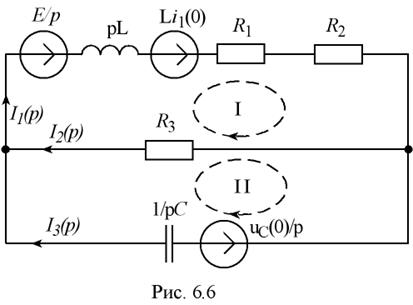
II.2. Для полученной операторной схемы замещения составляется система уравнений, по первому и второму законам Кирхгофа в операторной форме.

Для рассматриваемого примера эта система уравнений имеет вид

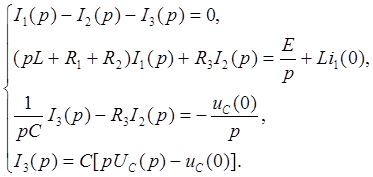
II.3. Преобразованная по Лапласу система уравнений решается относительно изображения искомой переменной (в рассмотренном случае относительно ). Решение должно быть представлено в виде отношения двух полиномов оператора p.

.

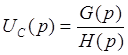При этом необходимо преобразовывать, чтобы в составе Н(р) множитель при р в наивысшей степени был бы равен единице, как это требуется при разложении дроби на простейшие.

II.4. По теореме разложения находится оригинал-закон изменения искомой переменной (в рассмотренном примере u_C(t) ). В простейших случаях оригинал можно находить по формулам соответствия f(t)^:=:F(p).

III Расчет, переходных процессов по методу переменных состояния.

В основу метода переменных состояния положена принципиальная возможность замены дифференциального уравнения n –го порядка электрической цепи системой из nдифференциальных уравнений первого порядка. При этом, в качестве переменных состояния, принимают токи в индуктивности i_L и напряжение u_C на емкостях, которые однозначно определяют запас энергии в любой момент времени. Переходный процесс в рассматриваемой цепи описывается системой дифференциальных уравнений в форме Коши и системой начальных условий.

Из системы уравнений 5.1 получаем

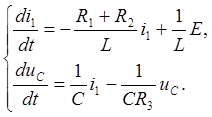
Подставим численные значения величин параметров цепи

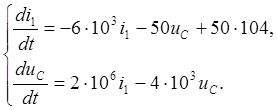                                 (6.16)

Находим  начальные условия

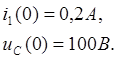                                                              (6.17)

Систему уравнений (6.16) необходимо решить численными методами. При численном способе решения уравнений состояния используют различные программы численного интегрирования на ЭВМ: метод Рунге-Кутта, метод Эйлера, метод трапеций и др. Так, например, в пакете программ MathCAD 2000 [5] приведены программы численного решения дифференциальных уравнений модифицированном методом Эйлера и методом Рунге-Кутта. Поскольку погрешность решения методом Эйлера достигает нескольких процентов, то более предпочтительным является метод Рунге-Кутта, который при решении уравнений четвертого порядка дает погрешность h^-4, где h — шаг приращения переменной. Этот метод обеспечивает контроль точности вычислений на каждом шаге интегрирования и программную регулировку шага.

Систему уравнений (6.16) и начальные условия (6.17) запишем в матричном виде.

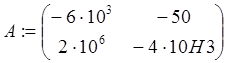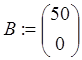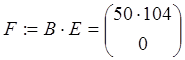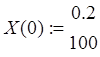,  , , , , где А ‑ собственные коэффициенты системы; В – вектор коэффициентов при воздействиях; X(0) ‑ вектор начальных условий; F – величина входных воздействий.

В системе MathCAD программа интегрирования уравнений по методу Рунге-Кутта имеет имя rkfixed. Обращение к ней производится  через оператор присвоения какой либо переменной (например z) имени программы:

z:=rkfixed(X,0,t_k,N,D),                                          (6.18)

где: x – вектор переменных состояния, размер которого определяется вектором начальных значений x(0); и соответствует числу уравнений состояния; 0 и t_k начало и конец временного интервала интегрирования; N – число точек на интервале интегрирования; D – функция, которая описывает правую часть уравнений, разрешенных относительно первых производных.

Для линейных цепей функция D  имеет вид линейного матричного преобразования

D(t, x)=Ax+F.                                                   (6.19)

Все элементы матриц А и F должны быть определены перед обращением к программе rkfixed.