Домашние задания по расчету электрических цепей: Методические указания, страница 11

2. Получение частотных передаточных функций по напряжению и току для фильтра, нагруженного на сопротивление Z_н=R_н, основывается на уравнениях четырехполюсника. Найдем частотную передаточную функцию по напряжению . Для этого воспользуемся уравнением четырехполюсника , где заменим .

Передаточная функция фильтра по напряжению

.

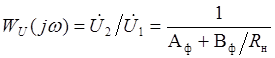Подставляя в выражения (4.2) и (4.3) численные значения величин, после преобразований получаем:

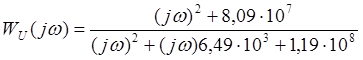 .                                   (4.11)

Аналогично можно найти передаточную функцию фильтра по току

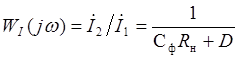,                                               (4.12)

где для симметричного П образного четырехполюсника  D=A. Подставляя численные значения в уравнение (4.12) получаем:

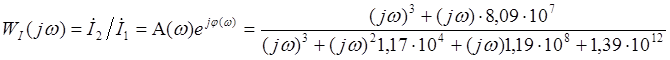.          (4.13)

Из найденной аналитической зависимости (4.13) получаем амплитудно ‑ частотную характеристику (АЧХ) H(w), представляющую модуль частотной передаточной функции  и фазочастотную характеристику (ФЧХ) , представляющую собой аргумент частотной передаточной функции .

На основании полученных зависимостей, с помощью  прикладных программ, необходимо рассчитать и построить АЧХ и ФЧХ фильтра (образец для варианта №30 приводиться в приложении 4). АЧХ и ФЧХ для фильтра варианта № 30 приводиться на рис. 4.5.

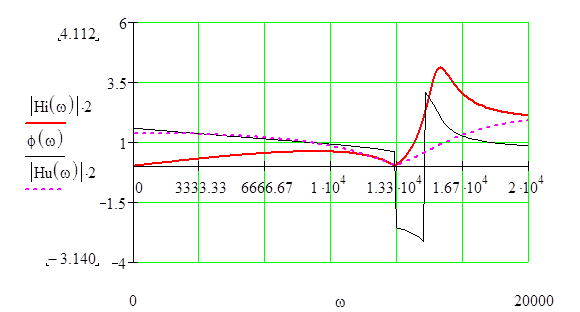
Рис. 4.5

где Hi(w) – представляет собой АЧХ фильтра по току, Hu(w) – АЧХ фильтра по напряжению и f(w) – ФЧХ исследуемого фильтра.

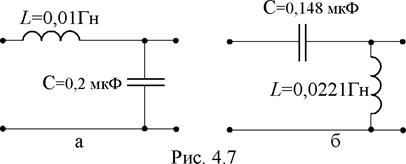
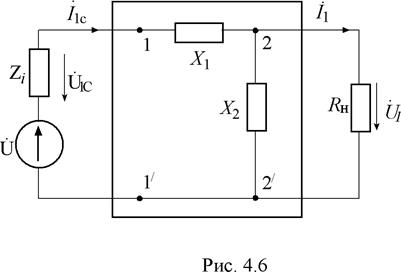3. Для согласования генератора и фильтра используем четырехполюсник, схема которого изображена на рис. 4.6.

На частоте согласования  сопротивление нагрузки R_н  равно характеристическому сопротивлению четырехполюсника, поэтому входное сопротивление фильтра и нагрузка согласующего четырехполюсника, равны R_н. Для передачи максимальной мощности от генератора к нагрузке должно выполнятся условие  где  ‑ число, сопряженное комплексу внутренного сопротивления  генератора, т.е. ; Z_вх – входное сопротивление согласующего четырехполюсника. Таким образом,

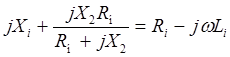.                                               (4.14)

Неизвестными в уравнении являются X₁и X₂. Приравнивая слева и справа вещественные и мнимые части, получаем систему уравнений

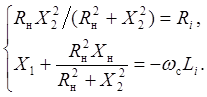
Решая систему уравнений, находим параметры согласующего четырехполюсника

.

Очевидно, что поставленному требованию одинаково удовлетворяют два различных согласующих четырехполюсника (рис 4.7). Однако первый из них (рис. 4.7, а) является низкочастотным фильтром, поэтому с целью сохранения полосы пропускания в дальнейших расчетах используем четырехполюсник по схеме рис. 4.7, б. Постоянные четырехполюсника

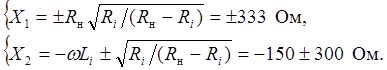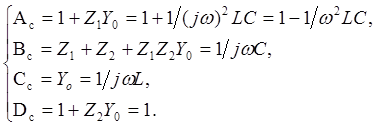                          (4.15)

При последовательном соединении двух четырехполюсников, матрица постоянных (A, B, C, D) эквивалентного четырехполюсника равна произведению матриц отдельных четырехполюсников, т.е:

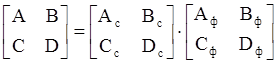 .                                          (4.16)

Найдем модуль коэффициента передачи по току эквивалентного четырехполюсника, для чего воспользуемся уравнением (рис. 4.1)

, где .

Модуль коэффициента передачи

.

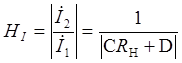Из уравнения (4.16) находим постоянные эквивалентного четырехполюсника

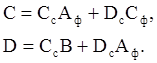
Используя формулы (4.2), (4.3), (4.4) и (4.15), после преобразований, находим

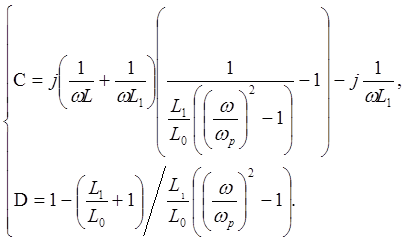
Подставляя численные значения, рассчитываем С и D для

, D=-1,298.

Таким образом, модуль коэффициента передачи по току

.

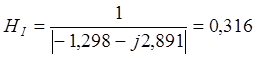Полученный коэффициент передачи приблизительно в три раза меньше аналогичных величин, рассчитанных в п. 1 и 2. Однако уменьшение H_I сопровождается увеличением активной мощности, выделяющейся в сопротивлении нагрузки.

Задание 5. Расчет переходных процессов В ЦЕПЯХ первого порядка

Исходные данные:

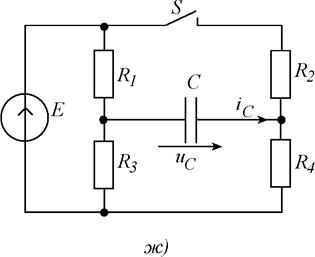
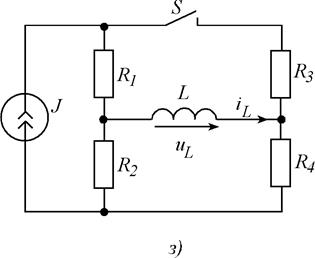
Для схем, изображенных на рис. 5.1, требуется рассчитать мгновенные значения величины (или всех токов и напряжений), указанной в таблице 6.1, после выполнения коммутации. Выбор схемы, параметров ее элементов и вида коммутации осуществляются с помощью табл. 5. 1, в соответствии с вариантом задания. Расчет выполнить классическим  и операторным методами.

 

     

         

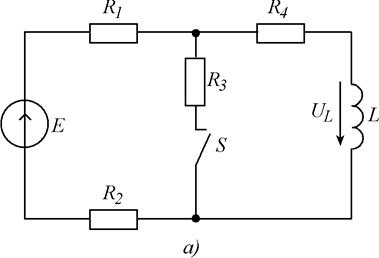
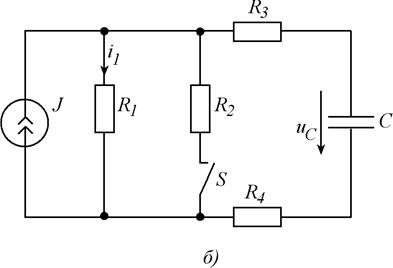
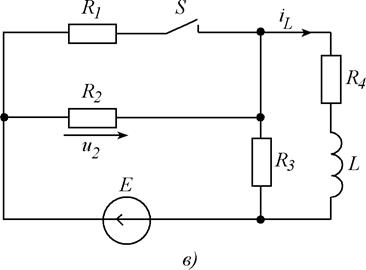
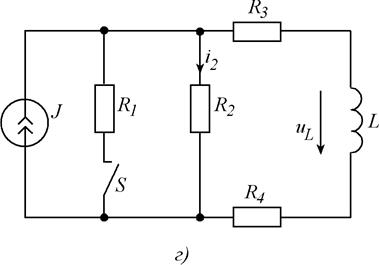
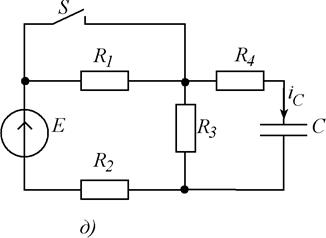
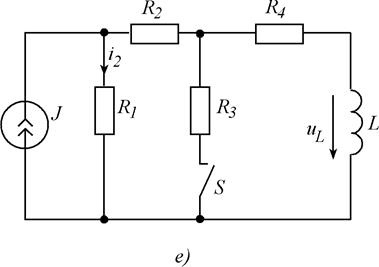
Рис. 5.1. Схемы заданий.