Домашние задания по расчету электрических цепей: Методические указания, страница 20

Таблица 7.2

Требуется:

1.  Найти магнитные потоки в ветвях ферромагнитного сердечника методом графического суммирования вебер-амперных характеристик.

2.  Проверить полученные результаты путем решения обратной задачи.

3.  Найти статическую индуктивность катушки при заданном токе.

Методические указания.

1. Выполнение задания следует начать с определения тока I в обмотке катушки. Для этого необходимо рассчитать нелинейную электрическую цепь. Воспользуемся сначала методом эквивалентного генератора, представив линейную часть цепи эквивалентным источником ЭДС.

Рассчитаем ЭДС Е_г этого источника как напряжение на зажимах а, б (см. рис. 7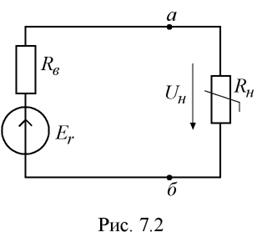.1) при отключенном сопротивлении R_н. Внутреннее сопротивление R_в этого источника находим как сопротивление между зажимами а, б при отключенном сопротивлении R_н и полагая, что внутреннее сопротивление данного источника напряжения U₀ равно нулю. В результате получим простую схему (рис. 7.2) для расчета тока I , протекающего через сопротивления R_н и обмотку катушки. По второму закону Кирхгофа имеем

E_г=R_в I+ U_н =R_в I + a I² ,

откуда .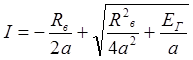

2. Второй этап выполнения задания - расчет магнитной цепи при известной магнитодвижущей силе Iw (прямая задача). Эта задача решается графическим методом -путем построения и соответствующего суммирования вебер-амперных характеристик участков цепи.

Рассмотрим порядок решения задачи, например, для случая, когда обмотка находится на первой ветви, а воздушный зазор – во второй ветви.

Определяем магнитное сопротивление воздушного зазора

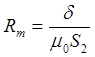, где  ‑ магнитная постоянная.

Вебер-амперную характеристику воздушного зазора

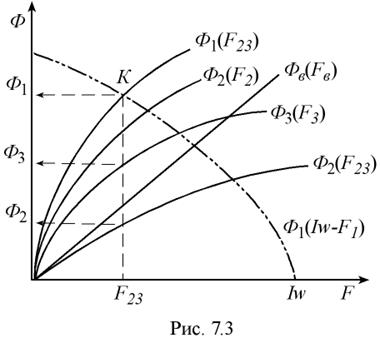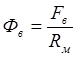
строим на графике рис.7.3 в видепрямой Ф_в(F_в).

Вебер-амперная характеристика стального участка второй ветви Ф₂ (F₂) строится по кривой намагничивания (см. табл. 7.2), учитывая, что Ф₂=ВS₂, F₂=Hl₂. Магнитодвижущая сила второй ветви

.

Так - как Ф₂=Ф_в , то, складывая абсциссы кривых Ф_в(F_в) и Ф₂(F₂), получим кривую Ф₂(F₂₃). Магнитодвижущая сила F₂₃ является общей для второй и третьей ветви. Строим вебер-амперную характеристику третьей ветви Ф₃(F₂₃), учитывая, что Ф₃=BS₃ , F₂₃=Hl₃.

Используя соотношение Ф₁=Ф₂+Ф₃ , складываем ординаты кривых Ф₂(F₂₃) и Ф₃(F₂₃)  и получаем кривую Ф₁ (F₂₃). Для первой ветви строим зависимость Ф₁(Iw-F₁), учитывая, что  и F₁=Hl . Точка К пересечения кривых Ф₁(F₂₃) и Ф₁(Iw-F₁) дает искомое значение магнитного потока Ф₁ в первой ветви, поскольку она удовлетворяет условию Iw-F₁=F₂₃ или Iw=F₁+F₂₃. Значения Ф₂ и Ф₃ определяются такжеиз графиков рис. 6.3 по найденному значению F₂₃.

3. Для  проверки правильности полученных результатов решаем обратную задачу - считаем заданным один из найденных магнитных потоков и находим соответствующую ему магнитодвижущуюся силу (Iw). Целесообразно задаться найденным значением Ф₂=Ф_в. Находим F_в=R_мФ_в, затем определяем индукцию в стальном участке второй ветви В₂= Ф₂/S_2.. По кривой намагничивания (табл.8) находим значение Н₂ , соответствующее В₂  и определяем F₂ =H₂l₂. Далее вычисляем F₂₃=F_в+F₂ , H₃=F₂₃/l₃ , по кривой В(Н) определяем B₃ и далее Ф₃=В₃S₃ . Поток в первой ветви Ф₁=Ф₂+Ф₃, индукция В₁ = Ф₁/S₁. По кривой В(Н) определяем Н₁, и затем F₁=H₁l₁ .Наконец, определяем магнитодвижущую силу обмотки Iw=F₁+F₂₃ . Полученный результат не должен отличаться от исходного значения МДС (Iw)_исх более чем на 5%.

Если отличие окажется больше 5%, то необходимо найти ошибку в вычислениях и графических построениях.

4. Статическая индуктивность катушки определяется по формуле

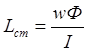, где Ф- значение магнитного потока в ветви, на которой размещена обмотка; I - ток в обмотке. В рассматриваемом примере Ф = Ф₁.

Библиографический список.

1.  Методические указания к домашним заданиям по расчету электрических цепей. Под редакцией А. П. Лысенко Л.: ЛМИ, 1984.

2.  В. А. Прянишников, Е. А. Петров, Ю. М. Осипов, Электротехника и ТОЭ в примерах и задачах, практическое пособие, 2001, СПб: «КОРОНА принт».

3.  В. А. Прянишников. Теоретические основы Электротехники. Курс лекций. СПб.: «КОРОНА принт» 2000.

4.  Т. А. Татур. Основы теории электрических цепей(справочное пособие). М. «Высшая школа». 1980.

5.  М. Херхагер, Х. Партолль, MathCAD 2000, Полное руководство, Пер. с нем. Киев: Изд. Группа BHV. 2000. 416 с.

ОГЛАВЛЕНИЕ

Задание 1	Расчет электрических цепей переменного тока по законам Кирхгофа и методом эквивалентных преобразований.
Задание 2	Расчет цепей переменного тока различными методами
Задание 3	Расчет цепей постоянного тока различными методами
Задание 4	Расчет электрических фильтров
Задание 5	Расчет переходных процессов первого порядка
Задание 6	Расчет переходных процессов второго порядка
Задание 7	Расчет нелинейных цепей
Приложение
Программы расчета электрических цепей переменного тока на MathCAD.
Программа расчета пассивных фильтров
Программа расчета переходных процессов методом Рунге- Кутта
Библиографический список